Практическое занятие по дисциплине ОДБ. Математика. Тема. Теорема о трёх перпендикулярах

Практическое занятие 16

Перпендикулярность прямых и плоскостей в пространстве

Тема. Применение теоремы о трех перпендикулярах. Решение задач.

Цель: продолжить формировать представление о перпендикуляре к плоскости, наклонной, основе наклонной, проекции наклонной на плоскость, расстоянии от точки к плоскости; сформировать представление о том, где используется перпендикулярность в реальной жизни, понятие перпендикулярности как основного принципа архитектуры; формировать умения представлять прямую, перпендикулярную к плоскости и решать задачи, применяя знания о перпендикулярности прямой и плоскости; формировать умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач по данной теме; формировать умение видеть математическую задачу в контексте проблемной ситуации в окружающей жизни; развивать пространственное мышление студентов, воспитывать математическую культуру. 

Оборудование: стереометрический набор, презентация PowerPoint к теме.

Литература

1.     Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10 – 11 классы: учеб. для общеоразоват. организаций: базовый и углубл. уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 3 – е изд. – М.: Просвещение, 2016. – 255 с.

2.     Чекова А.М. Агебра и начала анализа. 7 – 11 классы. Учеб. пособие. – Изд. 4-е, испр. и доп. – Х.: Країна мрій^тм, 2008. – 200 с.

3.     Генденштейн Л.Э., Ершова А.П. Математика. Наглядный справочник с примерами для школьников и абитуриентов. – Х.: «Гимназия», - 2002. 

4.     А.М. Колмогоров, О.М. Абрамов та др. Алгебра и начала анализа: Учеб. для 1011 кл. серед шк. – М.: Просвещение, 1993. 

5.     Пособие по математике для поступающих в вузы: Учеб. Пособ. Кутасов А.Д., Пиголкина Т.С., Чехлов В.И., Яковлева Т.Х.; под ред. Г.Н. Яковлева. – М.: Наука, 1985. – 480с.

6.     Погорєлов О.В. Геометрія. Стереометрія. Підручник за 10-11 кл. Київ : Освіта, 1994 – 128с.  

7.     Афанасьєва О.М., Бродский Я.С., Павлов О.Л. Геометрія 10 -11кл. : Пробний підручник. – Тернопіль: Навчальна книга – Богдан, 2004

Ход занятия

1. Актуализация опорных знаний студентов, мотивация обучения

1.1. Фронтальный опрос

•      Прямые в пространстве называются перпендикулярными?

•      Какие свойства прямой и плоскости, перпендикулярных между собой, вы знаете?

•      Сформулируйте признак перпендикулярности прямой и плоскости.

•      Сколько прямых, перпендикулярных к данной плоскости, можно провести через данную точку?

•      Сколько плоскостей, перпендикулярных к данной прямой, можно провести через данную точку?

•      Что такое перпендикуляр, опущенный из данной точки к плоскости?

•      Что такое наклонная, проводимая с данной точки к плоскости?

•      Дайте определение расстояния от прямой к параллельной ей плоскости.

•      Сформулируйте теорему о трех перпендикуляры.

1.2.   Проверка выполнения домашнего задания

1.3.   Минутка каллиграфии

1.4.   Устный счет. Игра

2. Сообщение темы и задач занятия

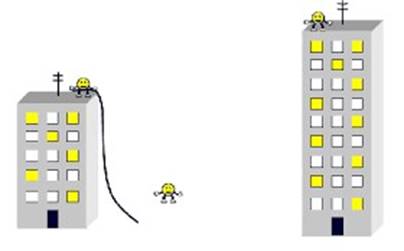При прокладке воздушной линии кабельной компьютерной сети между двумя зданиями (девяти- и пятиэтажка) начинающие монтажники столкнулись с проблемой – в наряде была указана высота зданий, между которыми нужно подвесить сетевой кабель, и проекционное расстояние между точками подключения, которое измерялось по земле между зданиями. Достаточно ли им получить на складе бухту кабеля длиной 27 м прежде, чем приступить к монтажу, если высота зданий 28 м и 14 м, расстояние между зданиями 20 м, запас на провис кабеля 2 м? 

Достаточно ли будет 22 метра? А 27 метров? Разница между высотами зданий 14 метров, может отрезать 14 метров кабеля? Или нужно считать по-другому?

 (20²+14²=596; √596=24,41 (м); 24,41+2=26,41 м) Достаточно 26,41 м

Можно ли использовать при рассуждении свойства «египетского» треугольника? (Можно, если принять сторону 14 близкой к 15 и рассуждать с допуском, тогда гипотенуза будет равна 25 м, еще 25+2 м запаса получим 27 м. Ответ: не более 27 метров понадобится.)

Какие геометрические понятия мы использовали при решении:

высота, длина, перпендикулярно, расстояние, теорема Пифагора, «египетский» треугольник. Все они нам знакомы на плоскости. Пришло время изучить, как ведут

себя перпендикуляр и наклонная в пространстве.

Сегодня на занятии мы продолжим изучение раздела «Перпендикулярность прямых и плоскостей». Главная цель нашего занятия – выяснить, что понимается под понятиями перпендикуляра и наклонной в стереометрии; изучить свойства расстояний от точки до плоскости, между параллельными плоскостями; между прямой и параллельной ей плоскостью, между скрещивающимися прямыми, научиться применять теорему о трех перпендикулярах при решении задач.

3.       Закрепление и осмысление изученного материала

3.1.              Мини-тестирование по теоретическим вопросам

Тестовая проверка усвоения определений.

3.2.              Решение задач (фронтально)

Задача № 1. Точка А не лежит в плоскости, а точка Е - принадлежит этой плоскости. АЕ =

13, проекция этого отрезка на плоскость равна 5. Каково расстояние от точки А до данной плоскости?

Решение.  АС²=АЕ²-СЕ²;  АС = 12 единиц.

Задача № 140 стр. 44. Из точки А, не принадлежащей плоскости α, проведены к этой плоскости перпендикуляр АО и две равные наклонные АВ и АС. Известно, что угол ОАВ равен углу ВАС и равен 60º, АО = 1,5 см. Найдите расстояние между основаниями наклонных.

Решение.

Рассмотрим прямоугольный ∆ОАВ: угол ОАВ 60º, угол АОВ= 90º, угол АВО

= 30º. Гипотенуза АВ равна удвоенному катету АО, как противолежащему углу

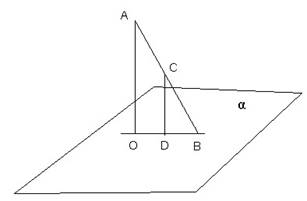30º. АВ = 1,5*2=3 (см). Рассмотрим равнобедренный по условию ∆ВАС: угол ВАС=60º, значит треугольник равносторонний, АВ=АС=ВС = 3 (см).

Ответ: ВС= 3 см - расстояние между основаниями наклонных.

Задача № 141 стр. 44. Один конец данного отрезка лежит в плоскости α, а другой находится от нее на расстоянии 6 см. Найдите расстояние от середины данного отрезка до плоскости α. Решение.

∆ АОВ и ∆СDВ подобны по двум углам, АС равно половине АВ, значит СD будет равно половине АО, 6/2= 3 см.  Ответ: 3 см.

             3.3.     Работа в группах (творческое задание)

Составить текст сказки о единственности прямой, проходящей через точку перпендикулярно данной плоскости.

3.4. Решение задач (самостоятельно)

Задача №5. (устно) Дан куб ABCDA₁B₁C₁D₁. Заполните пропуски о взаимном расположении прямых и плоскостей 

CC₁…DC;       AA₁…DCB;       D₁C₁…DCB;      B₁C₁…DD₁C₁;

D₁C₁…DC₁; A₁D₁..DC₁;  BB₁…AC; A₁B…BC; A₁B…DC₁.

Ответ: CC₁DC; AA₁DCB; D₁C₁ǀǀDCB; B₁C₁DD₁C₁; В₁C₁DC¹; A₁D₁DC₁;  BB₁AC; A₁BBC; A₁BǀǀDC₁.

Задача         №6.   (устно)       Дано:          ∆ ABC - прямоугольный; AM ⊥ AC; M ∉ (ABC)

Доказать: AC ⊥ AMB

Доказательство.

Т.к. AC ⊥ AB и AC ⊥ AM, а AM ⋂ AB, т.е. АМ и АВ лежат в    плоскости   АМВ, то AC ⊥ AMB       по      признаку перпендикулярности прямой и плоскости. Ч.т.д.

Задача №7. (устно) Дано: ВМDC - прямоугольник, M ∉ ABC, MB ⊥ AB

Доказать: CD ⊥ ABC

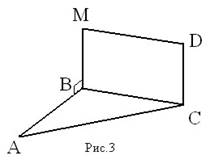Доказательство. 

MB ⊥ BC, т.к. ВМDC – прямоугольник, MB ⊥ AB по условию,  BC ⋂ AB, т.е. ВС и АВ лежат в плоскости АВС  ⇒  MB ⊥ ABC по признаку перпендикулярности прямой и плоскости. СD ∥ МВ по свойству сторон прямоугольника⇒ CD ⊥ ABC по теореме о двух параллельных      прямых,     одна из      которых перпендикулярна к плоскости (то и другая прямая перпендикулярна к этой плоскости).Ч.т.д.

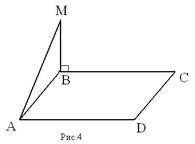Задача №8. (устно) Дано: АВСD – прямоугольник,

M ∉ ABC, MB ⊥ BC Доказать: AD ⊥ AM Доказательство.

1) ∠ABC =    90°,   т.к.    АВСD         –        прямоугольник ⇒ BC ⊥ AB, BS ⊥ MB по условию, MB ⋂ AB в точке В, т.е. МВ и АВ лежат в плоскости АМВ ⇒ BC ⊥ AMB по

признаку перпендикулярности прямой и плоскости. 2) BC ∥ AD (по свойству сторон прямоугольника) ⇒ AD ⊥ AMB по теореме о двух параллельных прямых, одна из которых перпендикулярна плоскости (то и другая прямая перпендикулярна к этой плоскости). 3) Т.к. AD ⊥ AMB ⇒ AD ⊥ AM по определению прямой, перпендикулярной плоскости. Ч.т.д.

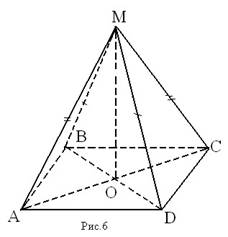Задача         №      9.       (устно)       Дано:          АВСD – параллелограмм, M ∉ ABC, МВ = МD, МА = МС Доказать: MO ⊥ ABC Доказательство.

1)       т.к. О –       точка          пересечения         диагоналей параллелограмма, то АО = СО и ВО = DO. ∆ BMD - равнобедренный, т. к. ВМ = МD по условию, значит МО - медиана и высота, т.е. MO ⊥ BD. 2) Аналогично доказывается в ∆ AMC: MO ⊥ AC. 3) Итак, MO ⊥ BD и MO ⊥ AC. А ВD  и  АС – пересекающиеся прямые, лежащие в плоскости АВС ⇒ MO ⊥ ABC по признаку перпендикулярности прямой и плоскости. Ч.т.д.

Рефлексия

•      Прямые в пространстве называются перпендикулярными?

•      Какие свойства прямой и плоскости, перпендикулярных между собой, вы знаете?

•      Сформулируйте признак перпендикулярности прямой и плоскости.

•      Сколько прямых, перпендикулярных к данной плоскости, можно провести через данную точку?

•      Сколько плоскостей, перпендикулярных к данной прямой, можно провести через данную точку?

•      Что такое перпендикуляр, опущенный из данной точки к плоскости?

•      Что такое наклонная, проводимая с данной точки к плоскости?

•      Дайте определение расстояния от прямой к параллельной ей плоскости.  Сформулируйте теорему о трех перпендикуляры.

Самооценивание

На радиальной диаграмме Венна изображены градации впечатлений от сегодняшнего занятия. Выберите для себя, как вы сейчас себя ощущаете.

.

Домашнее задание

1) [1] §19, 20   №   145, 157