Предел функции. Теоремы о пределах

Теоретическое занятие «Предел функции. Теоремы о пределах»

Определение. Число b называется пределом функции f(x) при х, стремящемся к а, если для любого положительного числа  найдется такое положительное число , что при всех ≠ , удовлетворяющих неравенству | − | < , справедливо неравенство | ( ) − | < . При этом употребляют

запись

                                                                        lim _→         ( ) =                                                       (1)

                Так как неравенство |      −    | <        равносильно двойному неравенству

−         <     <     +        , а неравенство | ( ) −        | <        - двойному неравенству

−        <     ( ) <          + , то определение предела функции в точке можно дать в

такой форме: число b есть предел функции f(x) при х, стремящемся к а, если, какова бы ни была − окресность точки b, найдется такая

− окресность точки а, что для любого значения ≠ , принадлежащего − окресности точки а, значение f(x) принадлежит − окресности точки b (рис. 1).

Из определения предела функции следует, что функция должна быть определена на промежутке ( −

,       +    ), кроме, возможно, самой точки а.

Теорема. Если функция f(x) имеет предел при х, стремящемся к а, то этот предел единственный.

Определение. Число b называется пределом функции f(x) при х, стремящемся к бесконечности, если для любого положительного числа  найдется такое положительное число , что при | | > , справедливо неравенство | ( ) − | < . При этом употребляют запись

                                                                          lim _→          ( ) =                                                      (2)

Вычисление предела функции f(x) следует начинать с подстановки предельного значения аргумента = в выражение, определяющее эту функцию

                                                                        lim _→         ( ) =     (а)                                              (3)

Приведем основные теоремы, на которых основано вычисление пределов элементарных функций.

1.     Если С - постоянная величина, то справедливы равенства 

                                                lim _→ С = С      и      lim _→ С ( ) = С lim _→                ( )                 (4)

2.     Если существуют пределы функций ( ) и ( ) , то:

lim _→ ( ( ) ± ( )) = lim _→            ( ) ± lim _→    ( )               (5) lim _→ ( ( ) ∙        ( )) = lim _→             ( ) ∙ lim _→       ( )                (6)

                                         lim _{→    →}         ( ) ≠ 0                                (7)

Следствие. Если n – натуральное число, то справедливы равенства

                                           lim _→ х    =             и       lim _→     √     = √                                  (8)

                    Если функция f(x) в предельной точке           =           не определена, то

нахождение предела путем подстановки предельного значения аргумента  в выражение, определяющее эту функцию может привести к одной из неопределенностей: 

                                                                  ∞ − ∞, 0 ∙ ∞,   , , 1       , 0 , ∞ .

Здесь могут оказаться полезными:

 первый замечательный предел

                                                                 lim _→     = 1 (х – радианная мера угла)                (9)

 второй замечательный предел

                                                                             lim _→     (1 +   )    =                                             (10)

                       предел отношения двух многочленов при     → ∞

                                                                                                                                     ∞, если       >    ;

... lim _{→              ...}             =        , если         =        ;          

                                                                                                                                     0, если        <    .

                                                                                                                                                                                                 (11)

Кроме того, при раскрытии неопределенностей используют следующие приемы:

1.     Сокращение дроби на критический множитель ( −        ) при →        .

2.     Избавление от иррациональности в числителе или знаменателе дроби.

3.     Разложение многочленов на линейные или квадратичные множители при        →    (         ≠ ∞)

Найдём пределы следующих функций:

                     1. lim _→      

r   Вычислим      предел        функции     ( ) =     путём         подстановки

предельного значения аргумента              = 4 в выражение, определяющее эту

функцию. Имеем lim _→      .▲

                     2. lim _→       

r   Числитель и знаменатель дроби неограниченно возрастают при

→ ∞, а значит, имеет место неопределенность вида . Разделив на х

                                                                                                                           lim         = lim         =

                   (         )(         )

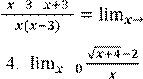lim _→=                                                       = 2. ▲

                                        →                    

r   Умножим числитель и знаменатель дроби на сумму ,

имеем                  _→   →   

. ▲

                      5. lim _→     

r   Используя первый замечательный предел, имеем 

lim _→       = lim _→     =       lim _→     =      . ▲

Задание        для         самостоятельного                 решения. Найдите пределы

функций:

7.