В. А. Дорофеев

Приближённые решения уравнений. Метод хорд.  

Рассмотрим задачу нахождения нулей функции f(x), т.е. корней уравнения f(x)=0. Предположим, что интересующий нас корень  изолирован, т.е., что найден содержащий его промежуток [a, b], в котором других корней нет.

Если на концах отрезка  [a, b] функция f(x) имеет значения f(а) и f(b) разных знаков, то по 1 теореме Больцано - Коши, деля на части а_k, b_k, содержащее корень, и определяя знак функции f в точках деления, можно произвольно сужать этот промежуток и таким образом осуществлять приближённое вычисление корня. Такой метод называется методом половинного деления. Однако этот приём, не смотря на его принципиальную простоту, на практике часто оказывается непригодным, так как требует слишком большого количества вычислений.

Рассмотрим основные приёмы приближённого вычисления изолированного корня уравнения f(x)=0. При этом будем использовать основные понятия и методы дифференцированного исчисления.

Теорема. Пусть выполнены следующие условия:

(1)                      функция f в промежутке [a, b] непрерывна вместе со своими производными  f ^(x) и f ^(х);

(2)                      значения f(а) и f(b) функции на концах промежутка имеют разные знаки f(а)f(b)0;

(3)                      обе производные f'(x) и f^(х) сохраняют каждая определённый знак на всём промежутке [a, b]. Тогда уравнение f(x)=0 на этом промежутке имеет единственный корень.

Следствия: Из непрерывности функции f и условия (2) следует, что между а и b содержится корень  уравнения f(x)=0. Так как производная f ^(x) сохраняет знак, то f в промежутке [a, b]возрастает или убывает и, следовательно, обращается в 0 лишь однажды, корень  изолирован.

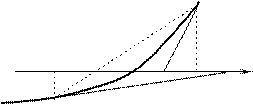
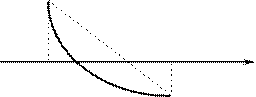
Условие (3) геометрически означает, что кривая y=f(x) не только идёт в одном направлении, но к тому же строго выпукла или вогнута, смотря по знаку f ^(х). На чертеже изобразим 4 возможных случая, соответствующих различным комбинациям знаков f ^(x) и f^(х). 

                                                   M1                                             M1                          

                          A       D                 T                                         D        A     

                 a                      T₁      b      x                             a                           b            x 

               M₂                                                                                                                                     M₂

                                                            I                                                                II

M  2                            M1                                                         

                     D                                                                                    D                                  

                 a                 A           b        x                             a       A                b               x 

     M₁                                                                                               M₂                          III                                    IV

1

         Приступим непосредственно к рассмотрению самого метода хорд.

Если промежуток [a, b] достаточно мал, то с приближением можно считать, что при изменении х в его пределах - приращение функции f(x) пропорционально приращению аргумента. Обозначая через  корень функции, имеем, в частности,

f () f (a)  a

 , откуда, с учётом того, что f()=0,  f (b) f (a) b  a

=a- (b  a) f (a) .

f (b)  f (a)

Таким образом, за приближённое значение корня принимается число x1  a  (b  a) f (a)   (1).

f (b) f (a)

Это выражение можно представить и в такой форме: x1  b  (b  a) f (b)  (2).

f (b)  f (a)

Изложенное правило получения приближённого значения корня называется правилом пропорциональных частей. Оно допускает простое геометрическое истолкование. Заменим дугу М₁М₂ хордой М₁М₂. Уравнение хорды может

                                           M₁                      быть записано в виде:

                                                                     f (b) f (a)                                                                      y f (a)  ba (xa).

    ^{D       A} Правило по существу сводится  к тому,   a                                       b          x  что вместо точки пересечения с осью

 ^M2  Ox дуги М₁М₂ мы находим точку пере        сечения с осью Oх её хорды.

Действительно, полагая в уравнении хорды y=0 для абсциссы х₁ точки D, мы получаем именно выражение (1). В связи с этим правило пропорциональных частей называют именно методом хорд.

Рассмотрим вопрос о положении точки х₁ по отношению к корню . Ясно, что точка х₁ лежит между а и b, но с какой стороны от  ? 

В случаях I и IV А левее D, а в случаях II и III - А правее D. Ограничимся случаями I и IV, применим снова выведенное правило, на этот раз к промежутку [x₁, b], заменяя в (1) а на х₁, получим новое приближённое значение корня : x2 _x1 _(bx₁) f (x₁⁾ , f (b) f (x₁)

содержащееся, по доказанному между х₁ и . Этот процесс можно продолжать неограниченно и построить последовательность возрастающих приближённых значений: a<x₁<x₂<…<x_n<…<.

При этом любые два последовательных значения х_n и х_n+1 связаны формулой:  xn1  xn  (b  xn) f (xn)    (3) . f (b)  f (x_n)

Очевидно, что lim x_n , т.к. (х_n)- возрастающая и ограниченная сверху числом

n

 последовательность. Если перейти к пределу в равенстве (3), используя при этом непрерывность функции f, то получим, что

2

(b) f ()

  0,

f (b) f ()

откуда f()=0. Т.к. других корней уравнения f(x)=0, кроме , в промежутке     [a, b] нет, то  = . Таким образом, применив достаточное число раз указанное выше правило, можно вычислить корень  с любой степенью точности. При этом остаётся открытым вопрос, как оценить точность уже вычисленного приближённого значения х_n. Для решения его применим к разности f(x_n)-f() формулу конечных приращений f(x_n)-f()=(x_n-)f'(c), <c<x_n (>c>x_n).

                                               f (xⁿ)                                           m наименьшее значение f '(x)в рас-

 Отсюда x _             , если обозначить через

f (c)

сматриваемом промежутке (которое можно вычислить), то получим оценку  f (x)

x_n-. Так по самой величине f(x_n) оказывается возможным судить о близо-

m

сти x_n к корню.

Пример. Уравнение х³-2х²-4х-7=0 имеет корень между 3 и 4, так как, если f(x)=x³-2x²-4x-7,     то      f(3)=-10<0, f(4)=9>0.    Вычислим этот   корень        с           точностью =0,01. В промежутке [3,4] обе производные f'(x)=3x²-4x-4 и f"(x)=6x-4 сохраняют знак "плюс". Наименьшее значение первой из них равно m=11.

                                                                      f (3)               10

Имеем: x₁  3    3    3  0,52...;  округляя, положим х₁=3,52. Т.к. f (4)  f (3) 19

f(3,52)= -2,246592, то по неравенству для оценки точности, требуемая точность ещё не достигнута.

Продолжаем: x2  3,52  0,48 f (3,52)  3,52  1,07836416  3,52  0,09..., или, f (4)  f (3,52)    11246592

округляя, х₂=3,61. Вычислим f(3,61)=-0,458319 и, пользуясь формулой оценки, снова видим,        что    цель ещё   не      достигнута.          Наконец, x₃  3,61_         0,39 ^ f (3,6)    _ 3,61_ 0,17874441 _ 3,61 0,0188... или, округляя, положим f (4)  f (3,61)   9,458319

х₃=3,63. Т.к. мы округлили в сторону корня, то могли и перескочить через него; что этого не произошло видно по знаку  числа  f(3,63)= -0,041653.

 На этот раз x₃ x₃  0,004. Таким образом, 3,630<<3,634, то есть =3,63+0,004.

3