Приближенные решения уравнений. Метод итераций.

В. А. Дорофеев

Приближенные решения уравнений. Метод итераций.

Рассмотрим вначале сущность итерационного метода. В отличие от прямых или точных методов, итерационные дают возможность получить решение лишь приближенно, путем повторения некоторой совокупности операций, позволяющей по исходному приближенному значению решения определить его уточненное значение. Выполнение этой совокупности операций составляет одну итерацию. Многократное повторение итераций позволяет получать все более точное решение при условии, что итерационный процесс сходится к искомому решению.

         Если данное уравнение

f(x)=0

приведено к виду

x=j(x), где |j'(х)|£r<1

всюду на отрезке [a, b], на котором оно имеет единственный корень, то исходя из некоторого начального значения х₀, принадлежащего отрезку [a, b], можно построить такую последовательность:

х₁=j(х₀), х₂=j(х₁),…, х_n=j(x_n-1),… .

 Пределом этой последовательности является единственный корень уравнения f(x)=0 на отрезке [a, b].Погрешность приближенного значения x_m корня  определяется неравенством:

.

Пример: Методом итераций решить с точностью до 0,01 уравнение x³-12x-5=0.

Здесь , , 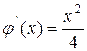то есть  в промежутке [-1,0] и поэтому метод итераций применим. Найдем теперь первое приближенное значение: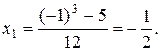

Найдём второе и последующие приближения:

;

;

.

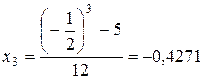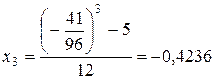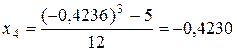Следовательно, искомый корень x»0,42.

Замечание 1. Уравнение y=f(x) можно записать иначе. Одним из самых распространенных представлений является представление в виде: x=x+cf(x), где с является произвольной постоянной.

Замечание 2. Для нахождения приближенного значения корня с погрешностью, не превышающей e, достаточно определить m так, чтобы выполнялось неравенство .