
В. А. Дорофеев
Приближённые решения уравнений.
Комбинированный метод хорд и касательных.
Рассмотрим задачу нахождения нулей функции f(x), т.е. корней уравнения f(x)=0. Предположим, что интересующий нас корень изолирован, т.е., что найден содержащий его промежуток [a, b], в котором других корней нет.
Если на концах отрезка [a, b] функция f(x) имеет значения f(а) и f(b) разных знаков, то по 1 теореме Больцано - Коши, деля на части аk, bk, содержащее корень, и определяя знак функции f в точках деления, можно произвольно сужать этот промежуток и таким образом осуществлять приближённое вычисление корня. Такой метод называется методом половинного деления. Однако этот приём, не смотря на его принципиальную простоту, на практике часто оказывается непригодным, так как требует слишком большого количества вычислений.
Рассмотрим основные приёмы приближённого вычисления изолированного корня уравнения f(x)=0. При этом будем использовать основные понятия и методы дифференцированного исчисления. Теорема. Пусть выполнены следующие условия:
(1) функция f в промежутке [a, b] непрерывна вместе со своими производными f (x) и f (х);
(2) значения f(а) и f(b) функции на концах промежутка имеют разные знаки f(а)f(b)0;
(3) обе производные f'(x) и f(х) сохраняют каждая определённый знак на всём промежутке [a, b]. Тогда уравнение f(x)=0 на этом промежутке имеет единственный корень.
Следствия: Из непрерывности функции f и условия (2) следует, что между а и b содержится корень уравнения f(x)=0. Так как производная f (x) сохраняет знак, то f в промежутке [a, b]возрастает или убывает и, следовательно, обращается в 0 лишь однажды, корень изолирован.
Условие (3) геометрически означает, что кривая y=f(x) не только идёт в одном направлении, но к тому же строго выпукла или вогнута, смотря по знаку f (х). На чертеже изобразим 4 возможных случая, соответствующих различным комбинациям знаков f (x) и f(х).
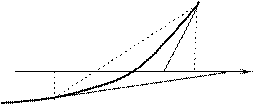 M1 M1
M1 M1
A D T D A
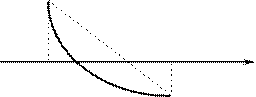 a T1 b x a
b x
a T1 b x a
b x
M2 M2
I II
M 2 M1

 D D
a A b x a
A b x
D D
a A b x a
A b x
M1 M2
III IV
1
Приступим непосредственно к рассмотрению самого метода.
Этот метод состоит в одновременном использовании, как метода касательных, так и метода хорд. Для определённости предположим, что мы имеем дело со случаем I.
y Приближенные значения x1 и x1' вычислим по формулам:
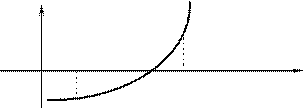 О
a b x x1
a
О
a b x x1
a
![]() (fb(b)a) ff((aa)), x1 b
(fb(b)a) ff((aa)), x1 b ![]() f'((bb)) , тогда по f
f'((bb)) , тогда по f
доказанному:a x1 x1' b. При следующем же шаге мы заменяем в этих формулах a и b на x1 и x1':
![]()
![]() x2 x1
x2 x1
![]() f;
x2' x1'
f;
x2' x1' ![]() f '.
f '.
![]() f
f
![]()
![]()
![]() Этот процесс
можно продолжать; имея два приближённых значения xn и xn',
между которыми содержится корень , мы
переходим к следующей паре приближенных значений по формулам: (xn' xn) f (xn); xn' 1 xn'
f '
Этот процесс
можно продолжать; имея два приближённых значения xn и xn',
между которыми содержится корень , мы
переходим к следующей паре приближенных значений по формулам: (xn' xn) f (xn); xn' 1 xn'
f '![]() .
.
xn 1 xn
f
![]() f
f ![]()
Таким образом, при комбинированном методе мы получаем одновременно с недостатком и с избытком приближённые значения корня, которые стремятся к точному с разных сторон.
Пример. Найти корни уравнения 2x3-x2-7x+5=0 с точностью до ε =0,001.
Решение: Подставляя целочисленные значения в выражение функции f(x)=2x3x2-7x+5, находим, что искомые корни содержатся в промежутках: 2 1 1, 0 2 1, 13 2.
Решим для первого неравенства, то есть в промежутке (-2,-1):
f '(x)=6x2-2x-7>0, f ''(x)=12x-2<0. Значит, имеем случай (II). Так как, f(-2)=-1<0, f(-
1)=9>0, то правило Ньютона применяем к левым концам промежутков. Имеем f'(2)=21 и следующие значения x1' и x1:
x1' 2 ![]() 1 1,952, x1
1
1 1,952, x1
1 ![]() 9 1,9
9 1,9
21 9 (1)
Округляя x1' в сторону уменьшения, получим число -1,96 > 1.
Если же округлить его в сторону увеличения, т.е. в сторону корня, то получим число -1,95; но f(-1,95)=0,01775>0, то есть в этом случае мы перескочим через корень. Это обстоятельство выгодно для нас, ибо даёт возможность сузить промежуток, содержащий корень, и отбросив прежнее значение x1, положить x1'= -1,96, x1= -1,95. Далее имеем f(-1,96)= -0,180672, f '(-1,96)=19,9696,
x2' 1,![]() ,96 0,00904...1,95095...,
x2 1,95
,96 0,00904...1,95095...,
x2 1,95
![]() 1,95 0,00089...1,95089....
1,95 0,00089...1,95089....
Поскольку 1 должно быть заключено между этими границами, то ясно, что 1 1,9509 0,0001, так что требуемая точность превзойдена.
Остальные случаи рассматриваются аналогично.
2
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.