В. А. Дорофеев

Приближённые решения уравнений.

Метод касательных (правило Ньютона).  

Рассмотрим задачу нахождения нулей функции f(x), т.е. корней уравнения f(x)=0. Предположим, что интересующий нас корень  изолирован, т.е., что найден содержащий его промежуток [a, b], в котором других корней нет.

Если на концах отрезка  [a, b] функция f(x) имеет значения f(а) и f(b) разных знаков, то по 1 теореме Больцано - Коши, деля на части а_k, b_k, содержащее корень, и определяя знак функции f в точках деления, можно произвольно сужать этот промежуток и таким образом осуществлять приближённое вычисление корня. Такой метод называется методом половинного деления. Однако этот приём, не смотря на его принципиальную простоту, на практике часто оказывается непригодным, так как требует слишком большого количества вычислений.

Рассмотрим основные приёмы приближённого вычисления изолированного корня уравнения f(x)=0. При этом будем использовать основные понятия и методы дифференцированного исчисления.

Теорема. Пусть выполнены следующие условия:

(1)                      функция f в промежутке [a, b] непрерывна вместе со своими производными  f ^(x) и f ^(х);

(2)                      значения f(а) и f(b) функции на концах промежутка имеют разные знаки f(а)f(b)0;

(3)                      обе производные f'(x) и f^(х) сохраняют каждая определённый знак на всём промежутке [a, b]. Тогда уравнение f(x)=0 на этом промежутке имеет единственный корень.

Следствия: Из непрерывности функции f и условия (2) следует, что между а и b содержится корень  уравнения f(x)=0. Так как производная f ^(x) сохраняет знак, то f в промежутке [a, b]возрастает или убывает и, следовательно, обращается в 0 лишь однажды, корень  изолирован.

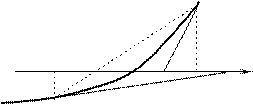
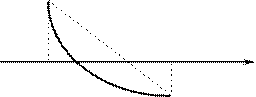
Условие (3) геометрически означает, что кривая y=f(x) не только идёт в одном направлении, но к тому же строго выпукла или вогнута, смотря по знаку f ^(х). На чертеже изобразим 4 возможных случая, соответствующих различным комбинациям знаков f ^(x) и f^(х). 

                                                   M₁                                             M₁                          

                          A       D                 T                                         D        A     

                 a                      T₁      b      x                             a                           b            x 

               M₂                                                                                                                                     M₂

                                                            I                                                                II

                                          M ₂                            M₁                                                         

            D                                          D                                           a                 A           b        x              a       A                b               x 

              M₁                                                                                                    M₂                         

                                                          III                                                                IV

1

         Приступим непосредственно к рассмотрению самого  метода касательных.

Пусть f удовлетворяет следующим условиям:

1)  f(x) непрерывна в [a, b] вместе со своими производными f', f”;

2)  f(a) и f(b) имеют разные знаки;

3)  обе производные f' и f" сохраняют каждая определённый знак во всём [a, b]. Кроме того, искомый корень f(x)=0 изолирован в [a, b]: a<<b. Отправляясь от какогонибудь из концов этого промежутка, например, от b, запишем формулу Тейлора с дополнительным членом в форме Лагранжа:

0  f ()  f (b)  f (b)(b)   f (c)(b)²,( c b) (1).

Отбрасывая дополнительный член, приближённо положим: f(b)+f'(b)(-b)=0, откуда f (b)  b       . Таким образом, мы приходим к приближённому значению корня  :

f '(b)

f (b)

x₁  b                                              (2). f '(b)

Получение этого значения можно наглядно использовать геометрически.

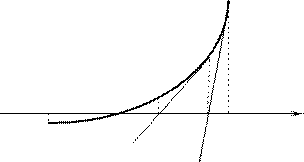                                                  M₂                   Рассмотрим касательную к кривой y=f(x) в                                                                        точке М₂ с абсциссой b. Её уравнение име                                                                     ет вид: y-f(b)=f'(b)(x-b). Полагая здесь у=0,                                                                        найдём абсциссу точки Т₁ пересечения ка сательной с осью Оx, она в точности сов        a                                     b             x       падает с точкой х₁, найденной выше. Зна          M₁                   T₂       T₁                          чит, суть дела в приближённой замене ду                                                         ги кривой М₁М₂ - касательной к ней в одном из её концов. Это правило носит имя  Ньютона, оно называется также методом касательных.

                                                                                                           Покажем, что если значение f(b) одного знака с f"(x), то х₁ лежит между  и b. f (b)

 Действительно, т.к. f(b) и f '(b) одного знака, то из x₁  b   ясно, что x₁<b. f '(b)

С другой стороны, из (1) и (2) следует:

                                                                                                         f (b)        1 f "(c)            ².

                                                                x₁ b                          (b)

                                                                                                         f '(b)        2 f '(b)

Но f"(x) в рассматриваемом случае имеет одинаковый знак с f '(x), следовательно, х₁<0  или <x₁<b.  Аналогично, если исходить из точки а, и касательную к кривой провести в точку f (a)

М₁(с абсциссой а), то взамен (2), получим приближённое значение x₁a  . Отf '(a) носительно вычисленного по этой формуле значения можно установить, как и выше: если значение f"(x) имеет одинаковый знак с f '(x), то x₁   лежит между а и . Таким образом, для каждого из четырёх возможных случаев понятно, с какого конца гарантирована успешность приближения к корню по правилу Ньютона. Повторное применение его в случаях I и IV дает последовательность убывающих значений:  b>x₁>x₂>…>x_n>x_n+1>…> , а в случаях II и III - последовательность возрастающих значений: 

2

a<x₁<x₂<…<x_n<x_n+1<…< .

Причём вычисление последующего значения по предыдущему  всегда производится по формуле:

_              f (xⁿ)  (3). x_{n 1}  x_n 

f '(x_n)

Покажем, что x_n . Монотонная и ограниченная последовательность имеет конечный предел . Переходя к пределу в  (1), с учётом непрерывности обеих функций f и f' f ()

найдём   , откуда f()=0 и =. Таким образом, правило Ньютона, поf ()

вторно применённое, позволяет вычислить корень  с любой степенью точности. При этом точность уже вычисленного приближённого значения оценивается по формуле:

f "( 2 f '(c)

                                                                              x_n1  1        c)  (x_n )².

 Обозначим через М наибольшее значение f "(x) в заданном промежутке [a, b] и через m- наименьшее значение f '(x) на [a, b]. Отсюда тогда получим: 

M2

xn1   xn . 2m

Поскольку справа стоит квадрат, этим обеспечено весьма быстрое приближение x_n к   (по крайней мере, начиная с некоторого места), что и делает метод касательных одним из самых эффективных методов приближённого вычисления корня.

 Замечание: Последнее неравенство выполняет ещё одну функцию. Если точность приближённого значения x_n уже найдена, то последнее неравенство позволяет оценить точность ещё не вычисленного значения x_n+1. Это может оказаться полезным при решении вопроса о том, на каком знаке целесообразно его округлять.

 Пример. Вычислить внутри отрезка [3,4] с точностью до ε=0,01 корень уравнения х³-2х²-4х-7=0,

Решение: f(x)=x³-2x²-4x-7, f(3)=-10<0, f(4)=9>0, f'(x)=3x²-4x-4>0,    f"(x)=6x-4>0 при 3 х 4. 

Наименьшее значение  f '(x) есть m=11. Отправляемся от b=4, так как в этом конце отрезка [3,4] знак f(x) совпадает со знаком f"(x). Тогда, используя формулу (2) f (4)     9

получим: x₁  4      4   4  0,32...; округляя, положим х₁=4-0,3=3,7. Т.к. f '(4)      28

                                                                                                                                f (xn )                            1,473

f(x₁)=f(3,7)=1,473, то по неравенству x_n  _                 имеем:  x₁    0,14, т.е.

                                                                                                                                    m                                  11

достигнутая                         точность                        недостаточна.                         Далее,

f (3,7)  1,473 x₂  3,7      3,7       3,7  0,066...; положим  x₂=3,7-0,066=3,634. На этот f '(3,7)  22,27

раз f(x₂)=f(3,634)=0,042…, так что в силу того же неравенства: x₂    0,004. Поэтому 3,630<<3,634 и =3,63 с требуемой точностью.

 Получение этого же результата методом хорд потребовало бы трёх шагов.

3