Программа курса по выбору «Геометрия на клетчатой бумаге» для учащихся 9 класса

Пояснительная записка

Предлагаемый курс призван развить творческие способности учащихся, расширить представление о теоретические и практические методы решения геометрических задач, ознакомить с нестандартными подходами к их решению.

Структура курса предполагает высокую активность учащихся, поскольку занятия построены как уроки-практикумы, что создает условия для постоянного самосовершенствования учеников. При изучении курса удачно используются приемы парной, групповой деятельности для выполнения элементов самооценки, взаимооценивания, умение работать с математической литературой.

Приобретенные знания, умения преодолевать трудности и самостоятельно решать достаточно сложные геометрические задачи пригодятся во время обучения в 10 классе, при дальнейшем обучении в профильных учебных заведениях.

Цель курса - привлечь учащихся к процессу решения достаточно сложных, интересных задач прикладного направления.

Задача курса:

• совершенствование математической культуры и творческих способностей учащихся на основе коррекции базовых математических знаний;

• развитие логического мышления учащихся и закрепление базовых математических понятий на уровне практического использования;

• расширение математических представлений по некоторым темам;

• формирование поисково-исследовательских навыков;

• развитие аналитического мышления, памяти, формирования умений преодолевать трудности при решении более сложных задач.

Изучение курса рассчитано на 12 часов в течение одного года, недельная нагрузка составляет 45 минут. Распределение может быть изменено учителем в зависимости от уровня подготовки учащихся, заинтересованности и профессионального направления.

 

Тематическое планирование

 

№ п/п	Наименование темы занятия	Количество часов
1	Вводное	1
2	Отрезки. Прямые. Углы.	1
3	Треугольники	1
4	Четырехугольники	1
5	Окружности	1
6	Симметрия	1
7	Площадь многоугольников	2
8	Площадь окружности	2
9	Задачи на разрезание	2

 

Занятие № 1. Вводное

Клетка – ты Чудо! Загадочна, проста и таинственна. Сколько возможностей открытий хранишь в себе, сколько закономерностей можно раскрыть, благодаря этому Чуду.

Существует много видов тетрадей: в клеточку, в линеечку, в ромбик , в кружочек. Но на уроках математики мы используем именно тетрадь в клеточку. В ней мы решаем различные задачи и строим геометрические фигуры. Помогает ли клетка при выполнении таких заданий?

Для того, чтобы понять, почему тетрадь по математике в клетку, мы узнаем побольше о квадрате.

Для того, чтобы понять, почему тетрадь по математике в клетку, узнаем побольше о квадрате. Из начальной школы помним, что у квадрата все стороны равны и все углы прямые. Если провести диагональ, то он разделится на два равных прямоугольных треугольника углами по 45⁰.

Проведем две диагонали. Квадрат разделился на четыре равных прямоугольных равнобедренных треугольника с острыми углами по 45⁰.  Если провести прямую через середины сторон квадрата, то он разобьётся на  два равных прямоугольника. Эти прямоугольники симметричны. У квадрата четыре оси симметрии.

Тетрадь в клетку очень удобна для занятия геометрией. Она помогает при построении различных геометрических фигур:

 

 

 

 Построение перпендикулярных прямых: Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.

 

 

 

Построение параллельных прямых: Две непересекающиеся прямые на плоскости называют параллельными. 

 

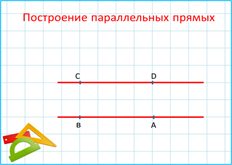
 Вывод: тетрадь в клетку помогает при построении геометрических фигур.

В древности слово «симметрия» употреблялось в значении «гармония», «красота». Действительно, в переводе с греческого это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей».

Посмотрим на кленовый лист, снежинку, бабочку. Их объединяет то, что они симметричны. У них есть ось симметрии. Если симметричную фигуру сложить вдоль оси симметрии, то её части совпадут.

У геометрических фигур может быть одна или несколько осей симметрии. В тетради в клетку легко построить симметричные фигуры.

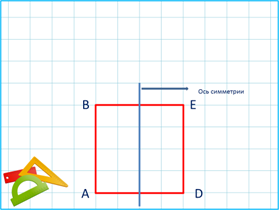
 Площадь многоугольника на клетчатой бумаге измеряется квадратными единицами: мм², см². Но в качестве единицы площади можно рассматривать и клетку.

 Нарисуем многоугольник с вершинами в узлах клеток и найду его площадь. Это можно сделать разными способами.

 1 способ.

 Будем пользоваться следующими правилами:

·                   Многоугольник всегда можно перекроить в любой другой многоугольник с такой же площадью. Такие многоугольники называются равновеликими.

·                   Если два многоугольника состоят из одинаковых частей, то они

 называются равносоставленными.

·                   Плоские равносоставленные многоугольники также являются

 равновеликими.

 Разделим многоугольник на части и составим из них равновеликий многоугольник с вершинами в узлах клеток, стороны которого проходят по линиям. В полученном многоугольнике легко посчитать количество клеток, то есть площадь многоугольника.

 

 

 Этот способ вычисления площади легко применим для многоугольников несложной конфигурации. А если он выглядит более причудливо? Оказывается, площади многоугольников, вершины которых расположены в узлах клетки, можно вычислить гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.

 

 2 способ. Формула Пика.

Формула Пика была открыта австрийским математиком Георгом Пиком в 1899г.

 Обозначим через В количество узлов внутри многоугольника, Г –

количество узлов на его границе. Тогда его площадь можно вычислить

по формуле: S = В + Г – 1.

 

 

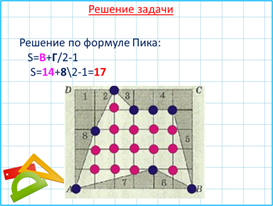
 Вывод: тетрадь в клетку помогает вычислять площади фигур.

Существует много различных и очень интересных задач на разрезание фигур. И я предлагаю вам их рассмотреть.

Задача 1: Разрежьте фигуру на 3 части так, чтобы сложить из них квадрат.

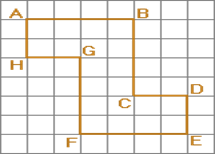
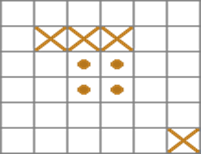
Задача 2: Разрежьте по клеточкам фигуру на 4 равные по форме и объему части так, чтобы в каждой был ровно
1 крестик и 1 точка.

Занятие № 2. Отрезки. Прямые. Углы.

 

1. Изобразите отрезок, длина которого равна √10 (стороны квадратных клеток равны 1).

Решение.

 

 

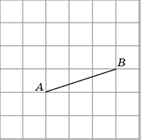
1.                 Через точку C проведите прямую, параллельную прямой AB.

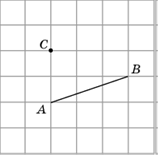
Решение.

 

2.                 Через точку C проведите прямую, перпендикулярную.

прямой AB.

 

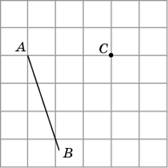
Решение.

3.                 На прямой c отметьте точки, удаленные от точки C на расстояние, равное √5 (стороны квадратных клеток равны 1).

Решение.

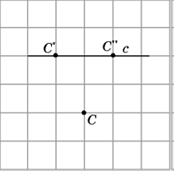
4.                 На прямой c отметьте точку C, равноудаленную от точек A и B.

 

Решение.

 

 

Занятие № 3. Треугольники

1.                 Изобразите треугольник со сторонами, равными √5, √10, √13 (стороны квадратных клеток равны 1).

Решение.

 

2.                 Изобразите прямоугольный треугольник, гипотенузой которого

является отрезок AB, а вершина C находится в одном из узлов сетки.

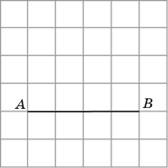
Решение.

 

3.                 Изобразите равнобедренный треугольник, боковой стороной которого является отрезок AB, а вершина C находится в одном из узлов сетки.

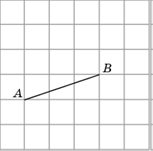
Решение

4.                 Изобразите точку пересечения медиан треугольника ABC.

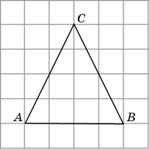
Решение.

5.                 Изобразите точку пересечения высот треугольника ABC.

 

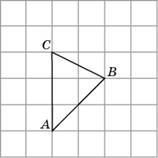
Решение.

 

Занятие № 4. Четырехугольники

 

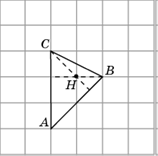
1.                 Изобразите квадрат ABCD, тремя вершинами которого являются точки A, B, C.

Решение.

 

2.                 Изобразите равнобедренную трапецию ABCD, тремя вершинами которой являются точки A, B, C.

Решение.

 

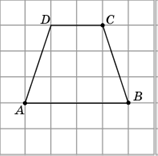
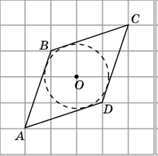
3.                 Изобразите параллелограмм ABCD, двумя вершинами которого являются точки A, B, а O – точка пересечения диагоналей.

Решение.

4.                 Изобразите прямоугольник, серединами сторон которого являются точки E, F, G, H.

Решение.

5.                 Изобразите трапецию ABCD, двумя вершинами которой являются точки A и B, а средней линией – отрезок EF.

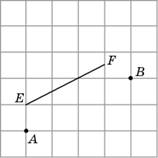
Решение.

 

 

 Занятие № 5. Окружности

1.                 Отметьте центр окружности, проходящей через точки A, B и C.

 

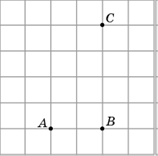
Решение

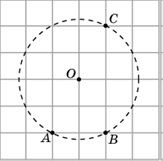
2.                 Отметьте центр окружности, описанной около треугольника ABC.

Решение

 

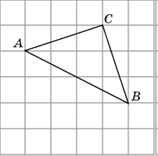
3.                  Отметьте центр окружности, вписанной в треугольник ABC.

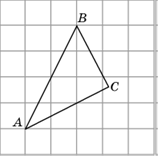
Решение

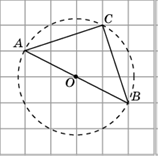
4.                 Отметьте центр окружности, описанной около четырехугольника

ABCD.

 

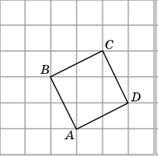
Решение

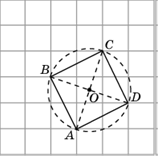
5. Отметьте центр окружности, вписанной в четырехугольник ABCD.

Решение

 

Занятие № 6. Симметрия

 

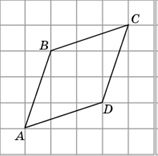
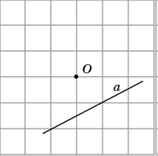
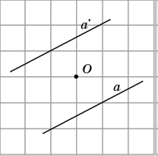
1.                 Изобразите прямую, симметричную прямой a относительно точки O.

Решение

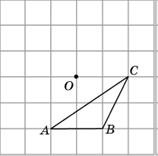
2.                  Изобразите треугольник, симметричный треугольнику ABC

относительно точки O.

 

Решение

 

3.                 Изобразите треугольник, симметричный треугольнику ABC относительно прямой c.

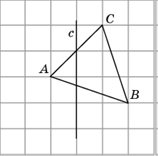
Решение

 

4.                 Изобразите треугольник, полученный поворотом треугольника ABC вокруг точки O на угол 90 против часовой стрелки.

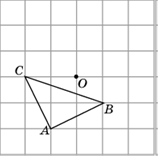
Решение

5. Изобразите четырехугольник, симметричный четырехугольнику ABCD относительно середины стороны CD.

                        Решение

 

Занятие № 7. Площадь многоугольников

 

Задача 1. На бумаге в клеточку 1 см х 1 см изображен четырехугольник ABCD. Найти его площадь в квадратных сантиметрах.

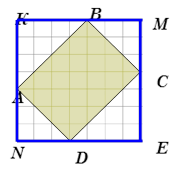
Решение

Найдем площадь фигуры как часть площади прямоугольника

S_ABCD = S_KMEN - S_∆АКВ - S_{∆ DCE} - S_∆AND - S_{∆ BMC}

Сначала найдем S_KMEN = 7  7 = 49 (cм²)

Далее вычислим площаль треугольников ∆АКВ, ∆DCE, ∆AND і ∆BMC.

S_∆АКВ =  АК  КВ =  4  4 = 8 (см²)

S_∆DCE =  CE  DE =  4  4 = 8 (см²)

S_∆AND =  AN  ND =   3  3 = 4,5 (см²)

S_∆BMC =   CM  BM =  3  3 = 4,5 (см²)

S_ABCD = 49 – 8 – 8 – 4,5 – 4,5 = 24 (см²)

Ответ: 24 cм²

По формуле Пика

І = 18, В = 14

S = І +  – 1

S = 18 +  – 1 = 24 (см²)

Ответ: 24 cм²

Задача 2. На бумаге в клеточку 1 см х 1 см изображен тругольник ABC. Найти его площадь в квадратных сантиметрах.

 

Решение

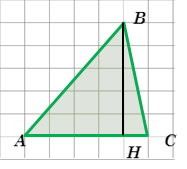
АC = 5 см, ВH = 5 см

 ВНАС =  5  5 = 12,5 (см²)

Ответ: 12,5 см²

 

По формуле Пика

 

І = 10, В = 7

S = І +  – 1 = 10 +  – 1 = 12,5(см²)

Ответ: 12,5 см²

Задача 3.

На бумаге в клеточку 1 см х 1 см изображена трапеция ABCD. Найти его площадь в квадратных сантиметрах.

Решение

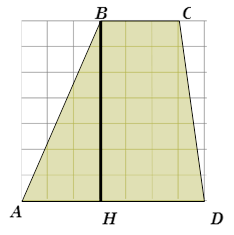
ВС = 3 см, АD = 7 см, ВН = 7 см,

 =  ВН =  7 = 35 (см²)

Ответ:: 35 cм²

По формуле Пика

 

 

 

 

                                                            І = 30, В = 12

S = І +  – 1 = 30 +  – 1 = 35(см²)

 Ответ: 35 cм²

Занятие № 8. Площадь окружности

 

Задача 1. На бумаге в клеточку 1 см х 1 см изображена окружность, R = 3 см Найти ее площадь в квадратных сантиметрах.

Решение

S = π R²= 9 π ≈ 28,26 (см²)

Ответ: ≈ 28,26 см²

По формуле Пика

 

І = 25, В = 4

S = І +  – 1 = 25 +  – 1 = 26 (см²)

Ответ: 26 см²

 

 Задача 2. На бумаге в клеточку 1 см х 1 см изображен сектор AОB, R = с.

Найти его площадь в квадратных сантиметрах.

Решение

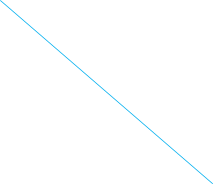
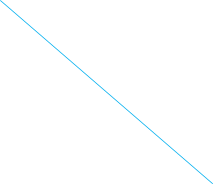
S_сек = S_круг =  π R²=  ≈ 7,06 (см²)

Ответ: ≈ 7,06 см²

По формуле Пика

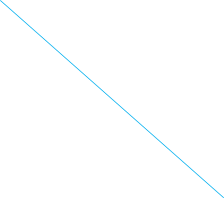
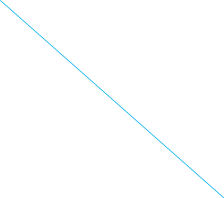
І = 4, В = 7

S = І +  – 1 = 4 +  – 1 = 6,5 (см²)

Ответ:: 6,5 см²

Задача 3. На бумаге в клеточку 1 см х 1 см изображено кольцо, R=3 см, r =1,5 см Найти его площадь в квадратных сантиметрах.

Решение

Рис.2.11

(3² – 1,5²) = 6,75 π ≈ 21,2 (см²)

Ответ: ≈ 21,2 см²

 

По формуле Пика

І = 16, В = 8

S = І +  – 1 = 16 +  – 1 = 19 (см²)

Ответ: 19 см²

Занятие № 9. Задачи на разрезание

 

Задача 1. Проведите линию, разрезав по которой треугольник, из полученных частей можно сложить параллелограмм.

Решение. Искомой линией является средняя линия DE треугольника АВС.

Задача 2. Трапецию разрежьте на три части, из которых можно сложить прямоугольник.

Решение. Искомыми линиями являются EF и EG.

Задача 3. Разрежьте закрашенную фигуру на четыре равные части.

Решение показано на рисунке.

Задача 4. Греческий крест разрежьте на несколько частей, из которых можно сложить квадрат.

Решение показано на рисунке.

Полученный квадрат показан на рисунке.

Задача 5. Разрежьте закрашенный шестиугольник на две равные части, из которых можно сложить квадрат.

Решение представлено на рисунке.

 

Скачано с www.znanio.ru