Радиантах мера угла

Радианная мера угла

На уроках геометрии Вы изучали окружность, её элементы, свойства. Окружность – это замкнутая линия, все точки которой равноудалены от центра. Радиус окружности - это отрезок, соединяющий её центр с любой лежащей на ней точкой. Мы узнаем, какая окружность называется тригонометрической; как осуществляется поворот точки вокруг начала координат.

Цели и задачи

Цель:

·         введение понятия тригонометрической окружности и поворота точки вокруг начала координат.

Задачи:

·         уметь определять координаты точки, лежащей на тригонометрической окружности;

·         объяснять зависимость угла от положения точки на тригонометрической окружности;

·         вычислять длину дуги окружности и площадь кругового сектора.

Узнаем, научимся, сможем

На уроке

мы узнаем:

·         о тригонометрической окружности; 

·         про поворот точки вокруг начала координат;

мы научимся:

·         определять координаты точки, лежащей на тригонометрической окружности;

·         вычислять длину дуги окружности и площадь кругового сектора;

мы сможем:

·         понимать определения градусной и радианной мер измерения углов.

Конспект урока

Алгебра и начала математического анализа.

Урок №___. Радианная мера угла

Перечень вопросов, рассматриваемых в теме:

Перечень вопросов, рассматриваемых в теме:

1) Понятие тригонометрической окружности;

2) Поворот точки вокруг начала координат;

3) Длина дуги окружности и площадь кругового сектора.

Глоссарий по теме

Окружность – это замкнутая линия, все точки которой равноудалены от центра.

Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.

Круг – часть плоскости, ограниченная окружностью.

Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.

Круговой сектор – часть круга, ограниченная двумя радиусами.

Угол в 1 радиан – центральный угол, опирающийся на дугу, равную по длине радиусу окружности.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Теоретический материал для самостоятельного изучения

На уроках геометрии мы с вами изучали окружность, её элементы, свойства. Повторим понятие окружности. Это замкнутая линия, все точки которой равноудалены от центра.

Радиусом окружности называется отрезок, соединяющий её центр с любой лежащей на окружности точкой.

На окружности можно выделить дугу. А если рассмотреть круг - часть плоскости, ограниченной окружностью - то можно выделить круговой сектор.

«Окружность бесконечно большого круга и прямая линия – одно и то же» Г. Галилей

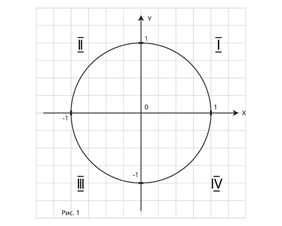
Действительно, и окружность и прямая – бесконечны. Рассмотрим окружность радиуса, равному 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической. (рис.1)

Длина этой окружности (в предыдущей задаче велотрека), как мы помним из уроков геометрии, . А учитывая, что R=1, , осями координат она поделена на четыре дуги, которые находятся соответственно в I, II, III и IV координатных четвертях.

Вычислите длину каждой дуги.

Ответ. длина каждой дуги равна  части окружности или 

Длина полуокружности равна  А так как образовался развернутый угол, то 180.

Рассмотрим дугу, равную по длине радиусу единичной окружности. Полученный центральный угол РОМ равен длине дуги МР=R.

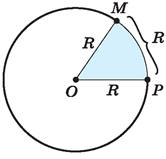    рис.3

Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.

Обозначается 1рад.

;

 α рад=(180/π α)° (1)

Длину дуги l окружности радиуса R (рис.4)

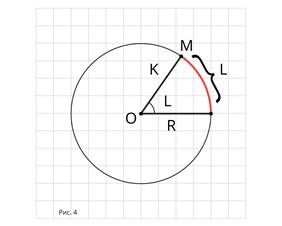
можно вычислять по формуле(3)

А площадь S кругового сектора радиуса R и дугой  рад (рис.5)

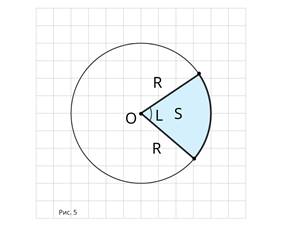
находят по формуле: , где (4)

Вернёмся к единичной окружности в координатной плоскости.

Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1; -1≤ у ≤ 1.

Введём понятие поворота точки. (рис.2)

1. Пусть  Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол 
2. Пусть  точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол - α.

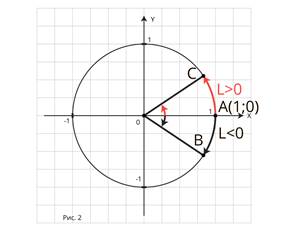
При повороте на 0 рад точка остаётся на месте.

Давайте рассмотрим такой пример:

при повороте точки М(1;0) на угол  получается точка N (0;1). В эту же точку можно попасть из точки М(1;0) при повороте на

угол  (рис.6)

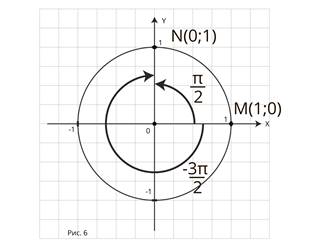
(рис.6)

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Найти градусную меру угла, равного  рад.

Решение: Используя формулу (1),

находим .

Так как , то  рад, тогда  (2)

Ответ: .

Пример 2. Найти радианную меру угла, равного 60.

Решение:

Вычисляем по формуле (2):  рад

 рад

При обозначении мер угла, наименование «рад» опускают.

Ответ:  рад,  рад.

Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера .

Решение: Используя формулу (3),

получим: 

Ответ: .

Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла .

Решение:

По формуле (4) вычисляем 

Ответ: 45  м²

Пример 5. Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный .

Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как то

прямоугольный равнобедренный треугольник ОМК имеет равные катеты и гипотенузу ОМ=R=1. По теореме Пифагора можно найти длины катетов. Они равны Учитывая, что точка М находится в I координатной четверти, её координаты положительны. 

На окружности можно найти координаты любой точки.

Ответ: 

Тренировочные задания:

1.       10⁰, 135⁰, -60⁰, 45⁰, -75⁰.

2.