Девятое ноября Задачи «на части»

(Делаем запись в тетради)

Учебник: страница 48-49 (ознакомиться с примерами решений задач, не записывать - устно).

Цели и задачи урока: научиться решать задачи «на части», научится выбирать наиболее рациональный способ решения.

Ребята, решите головоломку устно (см. подсказку ниже). 

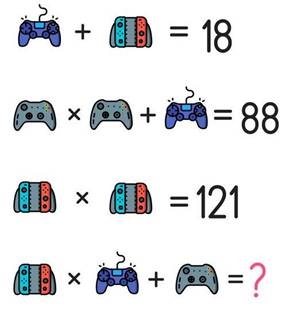
Подскажу вам, что начнем мы поиск неизвестных с третьей части головоломки, где число, умноженное само на себя, даёт в результате 121.

2

Когда мы умножаем число само на себя, выражение имеет вид: а·а=а , то есть мы возводим число во вторую степень (в квадрат). 

Посмотрите в таблицу квадратов чисел (на следующей страничке), она вам подскажет ответ: найдите в этой таблице число 121, а затем определите из скольких десятков и единиц будет состоять искомое число. Так, например, если посмотреть на выделенное жёлтым число, то мы видим, что нужно умножить 43 на само себя и получим 1849, то есть 43·43=1849. 

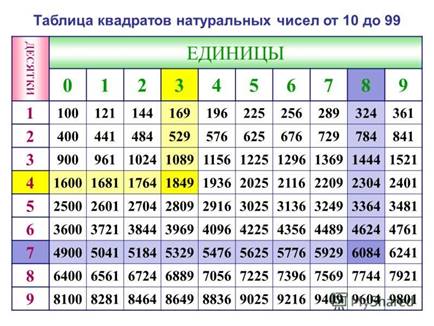
Далее решите самостоятельно.

Итак, вместо знака вопроса в головоломке мы напишем число 86. У всех так?

Что собой представляют задачи на части?

Это задачи, в которых говорится о том, что некое целое состоит и нескольких одинаковых частей. В этой ситуации находят величину одной части, а затем нужную величину.

Рассматриваемые в таких задачах величины состоят из частей. В некоторых из них части представлены явно, в других надо суметь выделить, приняв подходящую величину за 1 часть и определив, из скольких таких частей состоят другие величины, о которых идет речь в задаче.

Видеоматериал к уроку: https://resh.edu.ru/subject/lesson/685/  

Давайте запишем задачи из видео:

Задача №1

Условие: В черничное варенье кладут на каждые 10 кг ягод 3 кг сахарного песка. Сколько сахара нужно взять для получения 26 кг варенья?

Решение:

Итак, если взять один килограмм любого продукта (ягод или сахара) за одну часть, то у нас получится, что ягод - 10 частей, а сахара - 3 части. Узнаем, из скольких частей состоит варенье:

1)   10+3 = 13 (частей) - составляет всё варенье.

Узнаем, сколько килограммов вмещает одна часть. Для этого количество килограммов конечного продукта (26 кг варенья) разделим на количество частей, из которого оно состоит:

2)   26:13 = 2 (кг) – составляет одна часть.

Поскольку, сахара у нас 3 части, то узнаем, сколько килограммов составляют эти три части:

3)   3·2 = 6 (кг) – сахарного песка нужно для 26 кг варенья.

Ответ: в 26 килограммах варенья 6 кг сахарного песка.

                                                                                 (Делаем запись в тетрадочку)                                       

Задача №2

Смесь 1 кг орехов и 1 кг изюма стоит 400 рублей за килограмм, причем орехи в 3 раза дороже изюма. Сколько стоит килограмм орехов?

Решение:

Если всё измерять в стоимости килограмма изюма, то у нас имеется стоимость килограмма собственно изюма и, вместо стоимости килограмма орехов, возьмём стоимость трёх килограммов изюма (т.к. в условии сказано, что орехи в 3 раза дороже изюма).

Стоимость 1 кг орехов + 1 кг изюма такая же, как и 3 кг изюма + 1 кг изюма, т.е., столько же, сколько 4 кг изюма:

1кг изюма + 1 кг орехов = 400 р

1кг изюма + 1 кг орехов = 3 кг изюма + 1 кг изюма = 4 кг изюма

4 кг изюма = 400 р

Отсюда выясним стоимость одного кг изюма:

1)   400 : 4 = 100 (р) – стоимость 1 кг изюма или одной части.

Мы знаем, что орехи в 3 раза дороже изюма, выясним стоимость одного кг орехов:

2)   3 · 100 = 300 (р) – стоимость 1 кг орехов.

Ответ: 1 кг орехов стоит 300 рублей.

(Делаем запись в тетрадочку)

Задача №3

Я провел год в деревне, в Москве и в дороге. В Москве я провёл в 8 раз более времени, чем в дороге, а в деревне в 8 раз более, чем в Москве.

Сколько дней я провел в Москве, в деревне и в дороге?

Решение:

Примем за одну часть то время, которое он провёл в дороге, поскольку оно самое маленькое:

В дороге – 1 часть.

В Москве – 8 частей.

В деревне – 8·8 = 64 части.

Если сложить все эти части, то получится целый год, а в году 365 дней, если он, конечно, не високосный. Посчитаем, сколько частей будет составлять год:

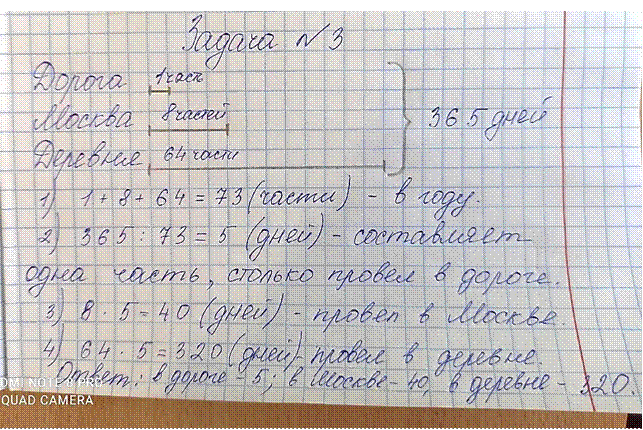
1)   1+8+64 = 73 (части) - в году.

Найдем, сколько дней составляет одна часть:

2)   365 : 73 = 5 (дней) – составляет одна часть, провел в дороге.

А теперь, найдем сколько дней составляют 8 частей (в Москве) и 64 части (в деревне):

3)   5 · 8 = 40 (дней) – провёл в Москве.

4)   5 · 64 = 320 (дней) – провёл в деревне.

Ответ: в дороге – 5 дней, в Москве – 40 дней, в деревне – 320 дней.

(Делаем запись в тетрадочку)

Задача №4.

 В Китае при обмене валюты за каждую операцию взимают комиссию 50 юаней. Чтобы заплатить комиссию только один раз, трое туристов решили сложить вместе свои деньги и обменять их как одну сумму. Первый дал 100 долларов, второй – 500 долларов, а третий – 400 долларов. Сколько юаней получит каждый при курсе 7 юаней за 1 доллар?

Решение:

За одну часть возьмём 100 долларов, поскольку это наименьшая сумма. Тогда:

У I туриста - 1 часть.

У II туриста - 5 частей.

У III туриста – 4 части. Сколько частей у всей суммы:

1)   1+5+4 = 10 частей.

Сосчитаем, сколько всего денег меняют туристы:

2)   100 + 500 + 400 = 1000 (дол.) – меняют.

Переведем 1000 долларов по курсу, узнаем, сколько получили бы туристы, если бы не комиссия:

3)   7 · 1000 = 7000 (юаней) – получаем до комиссии. Вычтем комиссию:

4)   7000 – 50 = 6950 (юаней) – получат туристы.

Узнаем, сколько юаней приходится на одну часть:

5)   6950 : 10 = 695 (юаней) – приходится на 1 часть, столько получит первый турист.

Зная, сколько юаней приходится на одну часть и сколько частей вложил каждый турист, вычислим, сколько денег получает второй и третий туристы:

6)   695 · 5 = 3475 (юаней) – получает II турист.

7)   695 · 4 = 2780 (юаней) - получает III турист.

Ответ: I – 695 юаней, II - 3475 юаней, III - 2780 юаней. 

(Делаем запись в тетрадочку) Фото на следующей страничке