Разработка урока "Исследование функции и построение ее графика"

05.05.2020.      Тема урока: Исследование функции и построение их графика.

 

 Цель: сформулировать понятие функции, выделить ее основные пути ее исследования, подготовиться к практической работе

 

Ход урока:

1. Прочитать теоретические сведения к уроку

2.Рассмотреть примеры описания функций

3. В тетради выполнить самостоятельную работу

4.  Качественное фото СВОЕЙ работы прислать на почту nata.kluy4nikova@yandex.ru

Указать в письме свои Ф.И.,  номер группы, дату урока пишем в конспекте!!!

 

 

Теоретические сведения урока:

 

 

 

 

 

 

 

 

 

 

 

 

 

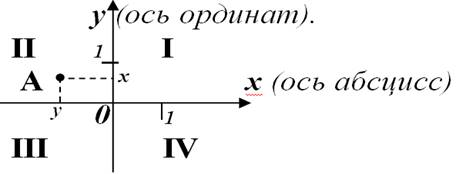
Ø  КООРДИНАТНАЯ ПЛОСКОСТЬ:                                                                                

Ø  ВЕЛИЧИНЫ            постоянные (константы);

                                  переменные                 независимые:  х

                                                                 зависимые (функция): у( х )

 

Ø  Если каждому значению независимой переменной соответствует единственное значение зависимой переменной, то такую зависимость называют функциональной зависимостью или функцией.

 

Ø  СПОСОБЫ  ЗАДАНИЯ  функции:  аналитический (формула), табличный, графический      

 

        

Ø  ГРАФИК ФУНКЦИИ –   множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции, т.е. множество  точек плоскости (х, у (х))

 

Ø  ПРЯМАЯ  пропорциональность:  функция вида у = kx, где  k¹ 0. График  функции у = kx – прямая, проходящая через  начало координат.

 

 

Ø ОБРАТНАЯ  пропорциональность:  y = ^k/_х  , где  k¹0, x¹0. График функции y = ^k/_х –  гипербола.

 

Ø ЛИНЕЙНАЯ  ФУНКЦИЯ:   у = kx+b, где  k и b -  заданные  числа.  График – прямая.

 

 

Ø  k - угловой коэффициент – он меняет  угол наклона графика функции у = kx  к оси  Ох. При  k>0  функция возрастает, при k<0 – убывает. При  k=0  график  функции y = b - прямая, проходящая через точку (0;b), параллельно оси Ох.

 

Ø Чтобы из графика  функции  у = kx  получить  график функции  у = kx+b, надо первый  график  параллельно  сдвинуть  вверх при  b>0, или  вниз  при  b<0.

 

 

Ø Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются, если одинаковы, то прямые -  параллельны.

 

Ø Область определения функции D(f) - множество всех значений, которые может принимать ее аргумент (т.е. х).

 

 

Ø Если функция задана формулой, то принято считать, что она определена при всех  тех значениях x, при которых эта формула имеет смысл, т. е. могут быть выполнены все действия указанные в выражении.

 

Ø Область значений функции Е(f) - множество значений ,которые

может принимать зависимая переменная, т. е. функция (т.е. у)

 

Ø 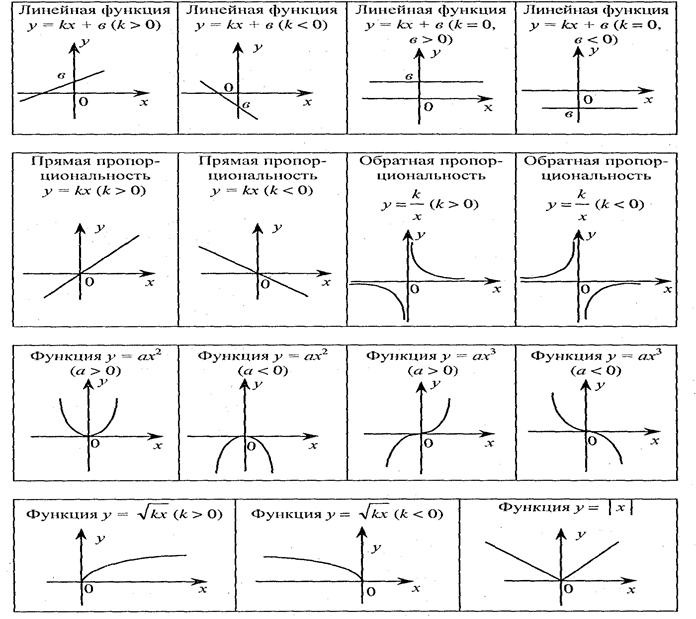ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ

 

 

1.

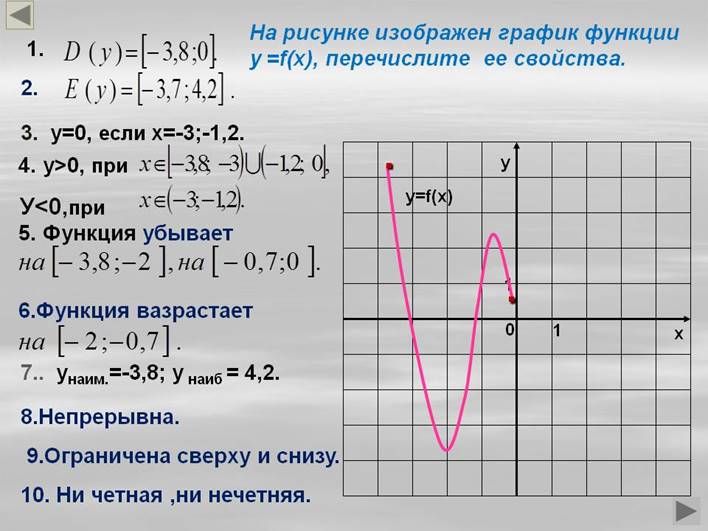
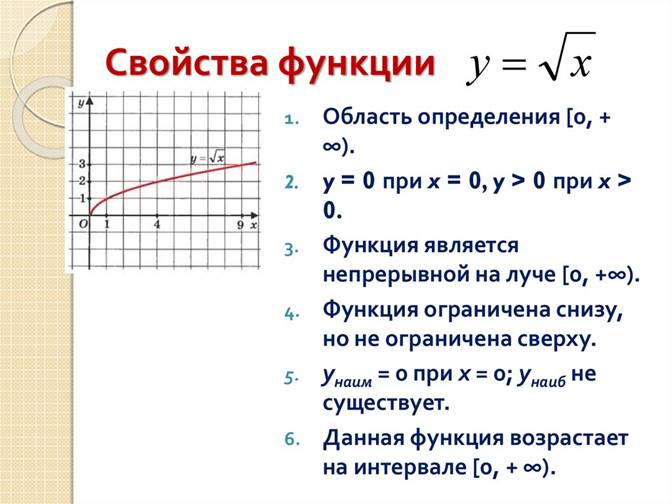
Еще раз рассмотрите примеры исследования функции:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

05.05.2020                     Самостоятельная работа по теме: Функция

 

 

1.       Что называется графиком функции?

2.      Какая функция называется возрастающей на промежутке?.

3.      Что называется областью значений функции?

4.      Найдите область значений функции у = х² + 2.

5.    Что называют нулями функции?

6.    Какая функция называется нечетной?

7.    Прочитайте график:

 

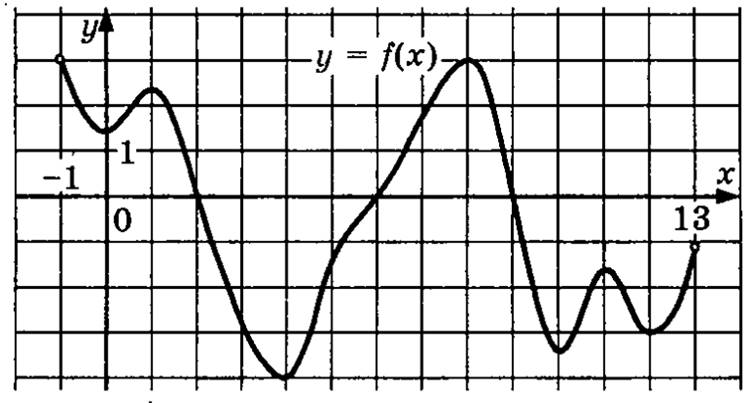
По графику укажите:

1.область определения

2.область значения

3.нули функции

4.промежутки возрастания

5.промежутки убывания

 

Скачано с www.znanio.ru