Девятнадцатое ноября

Решаем устно: 5+1=___

11-5=___

6·1=___

2+2·2=___ 24:4=___

3²-3=___

12-(3+3)=___

Что за элементарные примеры, которые решит даже первоклассник, спросите вы. Они и правда легкие, но вы заметили нечто необычное в этих примерах? Что их объединяет?

Конечно, результат во всех примерах одинаковый. Посмотрите, как поразному мы записали число 6: в виде сумы чисел, в виде разности, произведения, частного или другими способами. Всё это числовые выражения, т.е. число представили с помощью других чисел. 

Запишем тему урока:

Числовые выражения

Мы довольно часто встречаемся с заданиями типа «вычислить значение выражения». 

Что же такое числовое выражение?

Запись, которая состоит из чисел, знаков и скобок, а также имеет смысл, называется числовым выражением – запишем это определение.

Мы уже знакомы с числовыми выражениями. Сегодня нам предстоит обобщить и систематизировать все знания, которые мы получили ранее, а также научиться применять их на практике.

Например, записи 156 – 23 ∙ 5; 480 : 6 – 12; 230 + (45 – 12) – всё это числовые выражения.

                Просмотр                             видео                             по                           уроку:

https://resh.edu.ru/subject/lesson/7708/main/266123/  

Учебник: параграф 1.16 (стр. 56-57);

При вычислении значений числовых выражений следует руководствоваться следующими правилами.

1.                Если в числовом выражении требуется выполнить только сложение и вычитание или только умножение и деление, то эти действия выполняются по порядку слева направо.

2.                Если в числовом выражении есть скобки, то сначала выполняют все действия в скобках, а потом за скобками.

3.                Если в числовом выражении требуется выполнить несколько арифметических действий (сложение, вычитание, умножение, деление), то сначала выполняют умножение и деление (слева направо), а затем сложение и вычитание (слева направо).

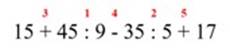
4.                Если в числовом выражении есть степень с натуральным показателем, то сначала нужно записать её в виде числа и только после этого приступать к выполнению остальных действий.

Так как в качестве знаков в числовых выражениях входят знаки арифметических действий, то мы можем посчитать значение числового выражения. Для этого необходимо выполнить указанные действия.

№1 

(записываем то, что синим)

Вычислим значение числового выражения:

(320 – 20) : 6.

Решим это выражение по действиям.

(320 – 20) : 6= 300 : 6 = 50

Часто для краткости записи не пишут полностью «значение числового выражения», а пишут просто «значение выражения», опуская при этом слово

«числового».

№2

(записываем то, что синим) Вычислим 62 – 5²+ 10 : 5.

Первым действием возведём 6 и 5 в квадрат, получим тридцать шесть и двадцать пять, а затем выполним все действия по порядку.

Нам уже известно, что на ноль делить нельзя. Про числовые выражения, которые содержат деление на ноль, говорят, что они не имеют смысла.

Например, выражение 12 : (4 ∙ 3 – 12) не имеет смысла, так как 

4 ∙ 3 – 12 = 0, а на ноль делить нельзя.

№3

(записываем то, что синим) Реши задачу, составив числовое выражение.

Условие:

Во время перемен между уроками Витя пробегает по коридорам лицея 30 км, причем на первой перемене он пробегает шестую, а на второй – пятую часть всей дистанции. Сколько километров пробежит Витя по коридорам лицея за первые две перемены, если ему ни разу не попадется завуч?

Решение:

Чтобы узнать, сколько он пробегает на первой перемене, нужно дистанцию за все перемены разделить на 6 (30:6).

Чтобы узнать, сколько он пробегает на второй перемене, нужно дистанцию за все перемены разделить на 5 (30:5).

Чтобы узнать, сколько пробежал Витя за эти две перемены, нужно сложить, получившиеся числа. 

Соберем это все в единое выражение: (30:6)+(30:5). Но нужны ли нам здесь скобочки? – Нет, ведь мы знаем порядок выполнения действий.

30:6+30:5=5+6=11 (км) – пробегает Витя за 1 и 2 перемены. Ответ: 11 км.

№4

(записываем то, что синим) Запишите и вычислите: а) сумму чисел 56 и 75 56+75=131;

б) разность чисел 66 и 42

66-42=24;

в) сумму квадратов чисел 9 и 7

Если требуется записать сумму квадратов, то для начала нам нужно каждое число возвести в квадрат, а потом сложить результаты:

9²+7²=9·9+7·7=81+49=130;

г) квадрат суммы чисел 6 и 7

Если требуется записать квадрат суммы, то для начала нам нужно узнать сумму чисел, а потом эту сумму возвести в квадрат. Поскольку возведение в степень выполняет по правилам первее, чем сложение, необходимо использовать скобочки: (6+7)²=13²=13·13=169;

д) разность квадратов чисел 6 и 2

Если требуется записать разность квадратов, то для начала нам нужно каждое число возвести в квадрат, а потом вычесть из первого второе:

6²-2²=6·6-2·2=36-4=32;

е) квадрат разности чисел 6 и 4

Если требуется записать квадрат разности, то для начала нам нужно узнать разность этих чисел, а потом эту разность возвести в квадрат. Поскольку возведение в степень выполняет по правилам первее, чем вычитание, необходимо использовать скобочки:

(6-4) ²=2²=2·2=4;

ж) сумму кубов чисел 5 и 2

Выполняется аналогично нахождению суммы квадратов (пример в), только меняем степень:

5³+2³=5·5·5+2·2·2=125+8=133; з) куб суммы чисел 5 и 6

Выполняется аналогично нахождению квадрата суммы (пример г), только меняем степень:

(5+6)³=11³=11·11·11=1331;

и) разность кубов чисел 5 и 1

Выполняется аналогично нахождению разности квадратов (пример д), только меняем степень:

5³-1³=5·5·5-1·1·1=125-1=124;

к) куб разности чисел 56 и 52

Выполняется аналогично нахождению квадрата разности (пример е), только меняем степень:

(56-52)³=4³=4·4·4=64.

№5

(записываем то, что синим)

Вычислите значение выражений удобным способом: а) 48·57+52·57=

Да, можно вычислять это в столбик, тратить на это много времени, но давайте приучим себя подобные примеры решать, вынося множитель за скобочки. Так правда легче, вы скоро привыкните упрощать себе этим жизнь.

48·57+52·57= мы умножаем оба числа на 57, вынесем множитель 57 за скобочки 57(48+52)=57·100=5700;

б) 145:5+455:5 = мы делим оба числа на 5, вынесем делитель 5 за

скобочки (145+455):5=600:5=120;

в) 2628:36+972:36= мы делим оба числа на 36, вынесем делитель 36

за скобочки (2628+972):36=3600:36=100.

Решить самостоятельно примеры б, г и д №267 из учебника на страничке 58, №272 (с числами из первого столбика) на страничке 59.

Записать в тетрадочку, фото с решениями прислать на Инфоурок.