Разработка урока по геометрии на тему "Объёмы многогранников и тел вращения." (11 класс)

Тема: Объёмы многогранников и тел вращения.

Автор: Сушкова Наталья Владимировна – учитель математики.

Цели:

• Обобщение, систематизация и контроль знаний формул объёмов и площадей поверхностей фигур и умений их применять для решения задач.
• Развитие навыков сравнительного анализа, логического мышления и воображения.
• Показать взаимосвязь математики с другими науками и окружающим нас миром.
• Воспитание коллективизма и настойчивости.

План.

1. Мотивация урока (слайд 2).

Блез Паскаль
Все наше достоинство — в способности мыслить. Только мысль возносит нас, а не пространство и время, в которых мы — ничто. Постараемся же мыслить достойно...

И не в какой-то конкретной области, а во всем, с чем нам придется соприкасаться…

Как вы знаете, геометрия возникла и развивалась в связи с потребностями практической деятельности человека. С древних времён люди сталкивались с необходимостью находить расстояния между предметами, определять размеры участков земли, ориентироваться по расположению звёзд на небе и т. п. Сегодняшняя наша тема ярко свидетельствует об этом. Приведу лишь несколько примеров, где встречается понятие объема.

—  (слайд 3). Например, комната в квартире имеет объём приблизительно 25-50 м³, объём воды в плавательном бассейне приблизительно 300-400 м³, если в нём 5 дорожек длиной 25 м. Объём огнетушителя всего 5 л, но количество образующейся при его работе пены 2000 литров, то есть 2 м³! По построенным в середине XX века нефтепроводам перекачивалось 4000 м³ в час, по современным – 9000 м³. С плотины гидроэлектростанции падает 30 млн. м³ в час.

—  (слайд 4). А насколько важно грамотно рассчитать объем необходимого воздуха на подводных лодках? Есть люди, которые следят за этими цифрами и от их знаний зависит не только качество выполняемой ими работы, но и зачастую жизни людей. Кто знает, может и ваша профессия будет связана с такими важными вычислениями. И Потому…

—  Сегодня на уроке нам предстоит повторить основные формулы для вычисления объёмов и площадей, решить задачи на их применение и подготовиться к выполнению самостоятельной работы. Работать нам предстоит как индивидуально, так в парах и всем классом.

—  И пусть, иногда кажется, что невозможно решить ту или иную задачу. На самом же деле просто надо приложить чуть больше усилий и желания.

—  (слайд 5). Умейте делать невозможное возможным, как Мориц Эшер в своих картинах.

2.   Приступим к повторению основных формул, знание которых нам поможет справиться с решением сегодняшних задач.

(слайд 6). Зная формулы объема для данных фигур, как бы вы могли их разделить на группы?

(слайд 7).

(слайд 8).

(слайд 9).

Как видите,  в каждой из формул присутствует такое понятие как площадь основания. Значит, важным этапом успешного решения задач на нахождение объема является умение находить площади основных фигур, не случайно это отразилось в одном из заданий ЕГЭ.

3. Рассмотрим некоторые примеры этого задания. (Разбор основных задач на нахождение площадей основных фигур.)

(слайд 10)

(слайд 11)

(слайд 12)

(слайд 13)

(слайд 14)

(слайд 15)

4. Основными знаниями владея, необходимо уметь их применить.

Рассмотрим несколько задач. (решение задач осуществляется на интерактивной доске).

(слайд 16). Задача №1: Прямоугольный параллелепипед описан около сферы радиуса 2. Найдите его объем.

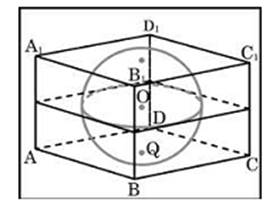
(слайд 17). Задача №2: В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. боковые рёбра равны  . Найдите объём цилиндра, описанного около этой призмы.

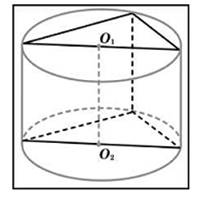
(слайд 18). Задача №3: Цилиндр и конус имеют общее основание и высоту. Вычислите объём цилиндра, если объём конуса равен 25.

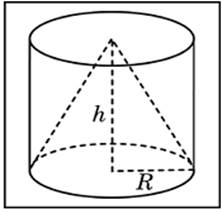
(слайд 19). Задача №4: стороны основания правильной четырёхугольной пирамиды равны 10, боковые рёбра равны 13. Найдите площадь поверхности этой пирамиды.

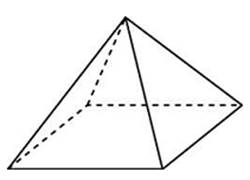
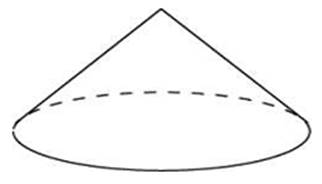
(слайд 20). Задача №5: Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90⁰. Вычислите объём конуса, делённый на π.

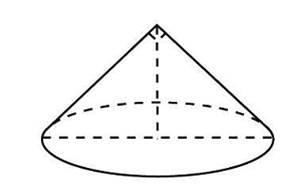
(Слайд 21). Задача №6: Найдите объём конуса, площадь основания которого равна 2, а образующая равна 6 и наклонена к плоскости основания под углом 30⁰.

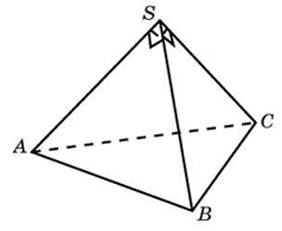
(Слайд 22)!!! Задача №7: Боковые рёбра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объём пирамиды.

 (Задача сопровождается картонной моделью, план решения составляется совместно с учащимися. Вычисления не проводятся. Затем пирамида переворачивается и звучит вопрос: «А как найти объём такой фигуры?»)

—  (Слайд 23) Готфрид Вильгельм Лейбниц 
 Мудрому не свойственно тратить силы сверх надобности.

(слайд 24) Только сложив из отдельных идей полное решение задачи можно увидеть всю его красоту…

И это понимает каждый, кто смог довести сложное решение до логического завершения. Не бросайте начатых дел!

5. Домашнее задание. Домашнее задание у вас состоит из задач, которые ещё раз помогут вам вспомнить основные факты и подходы к вычислению объемов.

6.      Домашнее задание

№1. Найдите площадь фигуры

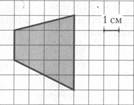
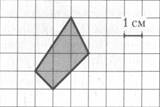
№2. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁  известно, что  D₁C₁ = 1, BB₁ = 2, B₁C₁ = 2. Найдите длину диагонали C₁A.

№3. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 10 и 5. Диагональ  параллелепипеда равна 15. Найдите площадь поверхности параллелепипеда.

№4.  Около шара описан цилиндр, площадь поверхности которого равна 3. Найдите площадь поверхности шара.

№5. В правильной четырехугольной призме диагональ равна  d и наклонена к плоскости боковой грани под  углом  α. Найти площадь боковой поверхности призмы.

7.      А сейчас давайте подведем итоги сегодняшнего урока.

Отмечу, что мне очень понравилась ваша работа на уроке и хочу вам всем без исключения сказать спасибо. Молодцы.

А завершить урок хотелось бы, услышав ваши продолжения следующих предложений:

(слайд 25)

• Больше всего мне понравилось ……………………….
• У меня пока не совсем получается…………………….
• Сегодня я понял(а), что мыслить ……………………….
• Сегодняшний урок показал мне ………………………