Решение логарифмических неравенств методом замены переменной.

Тема урока : « Решение логарифмических неравенств введением вспомогательной переменной» .

ОПРЕДЕЛЕНИЕ

Неравенства, которые содержат переменную под знаком логарифма или в его основании, называются логарифмическими.

Решение логарифмических неравенств основано на строгой монотонности логарифмической функции. Известно, что

·         при основании, большем единицы (a>1), логарифмическая функция возрастает (т.е. большему значению аргумента соответствует большее значение функции, ).

·         при положительном основании, меньшем единицы(0<a<1),  логарифмическая функция убывает (т.е. большему значению аргумента соответствует меньшее значение функции, ).

Имен­но мо­но­тон­ность ло­га­риф­ми­че­ской функ­ции поз­во­ля­ет ре­шать про­стей­шие ло­га­риф­ми­че­ские нера­вен­ства.

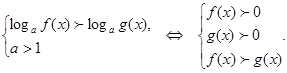           и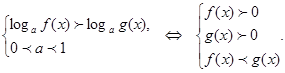                   

Решение простейших логарифмических неравенств мы рассматривали на прошлой лекции, сегодня еще один подход к решению логарифмических неравенств.

Некоторые логарифмические неравенства можно решить методом замены переменной. Рассмотрим несколько примеров на применение данного метода:

Пример 1: Решить неравенство

Решение :  ОДЗ: х>0

 Введем замену   , тогда получим неравенство или

Сделаем  обратную замену , т.к. основание логарифма 10>1

Ответ:

Пример 2: Решить неравенство

Решение:

ОДЗ: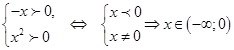

К первому логарифму в левой части неравенства применим свойство логарифма степени:

С учетом ОДЗ, получим:

 Введем замену   , тогда получим неравенство или

Делаем обратную замену: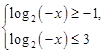

Так как основание логарифмов больше 1, то знаки неравенств сохраняются и получаем систему:

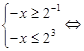
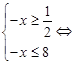
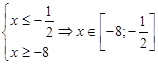
Пересечение с ОДЗ дает этот же промежуток.

 Ответ:

Пример 3: Решить неравенство  

Решение:

ОДЗ: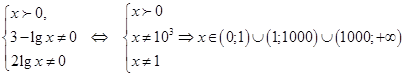 

Введем замену , тогда неравенство примет вид:

Перенесем все влево и сведем к общему знаменателю:

Получим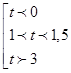  

Делаем обратную замену и возвращаемся к первоначальной переменной :

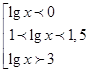
Так как основание логарифмов больше 1, то знаки неравенств сохраняются и получаем: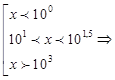

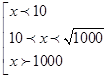
 Пересекая с ОДЗ, окончательно имеем:  .

Ответ:

Пример 4: Решить неравенство

Решение:

 ОДЗ:

Используя свойство логарифма степени и формулы замены основания, приведем второй логарифм к основанию 3

Введем замену , тогда неравенство примет вид:

 при любом значении t, так как дискриминант квадратного трехчлена .

Следовательно 

Перейдем к х, для этого делаем обратную замену:  Так как основание логарифмов больше 1, то знаки неравенств сохраняются. Пересекая с ОДЗ, окончательно имеем промежуток: .

Ответ:

Пример 5: Решить неравенство

Решение:

ОДЗ: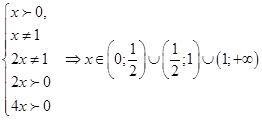

Используя формулы замены основания, приведем все логарифмы в рассматриваемом неравенстве к логарифмам по основанию 2:

Распишем полученные логарифмы, используя свойство суммы логарифмов:

Введем замену , тогда неравенство примет вид:

Имеем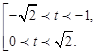  Сделаем обратную замену: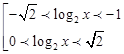  

Так как основание логарифмов больше 1, то знаки неравенств сохраняются: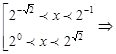

То есть С учетом ОДЗ, окончательно имеем:

Ответ:

 Пример 6: Решите неравенство

Решение:

ОДЗ: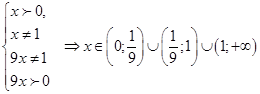

Используя формулы замены основания, приведем все логарифмы в рассматриваемом неравенстве к логарифмам по основанию 3:

Введем замену , тогда неравенство примет вид:

Имеем    Сделаем обратную замену:

 Так как основание логарифмов больше 1, то знаки неравенств сохраняются: 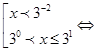 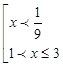С учетом ОДЗ, окончательно имеем:

Ответ:

 Пример 7:   Решите неравенство

Решение:

ОДЗ:

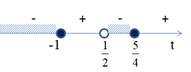Введем замену , тогда неравенство примет вид:

Имеем 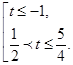   Сделаем обратную замену:  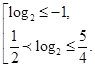Так как основание логарифмов больше 1, то знаки неравенств сохраняются: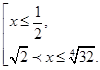

 С учетом ОДЗ, окончательно имеем:  

Ответ:

Пример 8:   Решите неравенство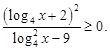

Решение:

ОДЗ:

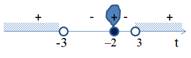Введем замену , тогда неравенство примет вид:

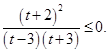
Имеем 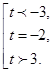   Сделаем обратную замену:  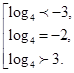Так как основание логарифмов больше 1, то знаки неравенств сохраняются: 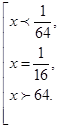 С учетом ОДЗ, окончательно имеем:

Ответ:

Скачано с www.znanio.ru