Решение систем линейных уравнений методом Крамера

Министерство образования Чувашской Республики

Государственное автономное профессиональное

образовательное учреждение Чувашской Республики

 «Чебоксарский техникум транспортных и строительных технологий»

Методическая разработка занятия по ЕН.01 Математика

На тему: Решение систем линейных уравнений методом Крамера.

Разработала:

преподаватель математики

Андреева Н.А.

Чебоксары

2024

Андреева Н.А. Методическая разработка учебного занятия по дисциплине ЕН.01 Математика для изучения темы «Решение систем линейных уравнений методом Крамера» студентами 2 курса учреждений среднего профессионального образования: План - конспект занятия.

– Чебоксары: ГАПОУ «ЧТТСТ» Минобразования Чувашии, 2024. - 14 с.

Методическая разработка учебного занятия по дисциплине ЕН.01 Математика на тему «Решение систем линейных уравнений методом Крамера» с применением основных методов обучения: фронтальный, проблемный, частично-поисковый, наглядно-иллюстративный, информационно-коммуникационный.

Цель изучения данной темы:

-углубить знания студентов по теме «Решение систем линейных уравнений», изучить решение систем линейных уравнений c помощью метода Крамера, научить решать системы линейных уравнений используя метод Крамера;

- развивать у обучающихся логического мышления, памяти, умению сравнивать, обобщать, анализировать, интереса к избранной специальности;

- воспитывать у обучающихся чувства ответственности, исполнительности, аккуратности, чувство гордости за избранную профессию, положительное отношение к знаниям, учениям,

интерес к математике.

Содержание

Пояснительная записка ………………………………………………………..4

Учебно-методическая карта урока…………………………………………….5

План урока………………………………………………………………………6

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Данная методическая разработка предназначена для проведения учебного занятия по дисциплине «Математика» на тему «Решение систем линейных уравнений методом Крамера» для студентов второго курса по программе учебной дисциплины, разработанной на основе Федерального государственного образовательного стандарта для специальностей среднего профессионального образования.

В результате изучения темы студент должен:

знать:

решение систем линейных уравнений методом Крамера;

применение знаний при решении систем линейных уравнений.

Уметь:

решать системы двух линейных уравнений с двумя неизвестными методом Крамера

решать системы трех линейных уравнений с тремя неизвестными методом Крамера

При разработке данного урока в зависимости от специфики подготовки студентов можно внести дополнения и изменения в содержание, последовательность изучения материала урока и распределение времени.

Наблюдается связь истории с математикой, при изучении материала использована задача прикладного характера для будущей практической деятельности, что прививает интерес к предмету. Данная методическая разработка содержит: учебно-методическую карту, ход, где сформулированы цели занятия и последовательность проведения урока, указан список литературы.

При проведении занятия, использованы учебные пособия, технические и наглядные средства обучения

УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА

Дисциплина: ЕН01.Математика

Тема занятия: Решение систем линейных уравнений методом Крамера

Вид занятия (тип урока): Комбинированный

Цели урока:

Дидактическая:

Повторить пройденный материал, углубить знания студентов по теме «Решение систем линейных уравнений», изучить решение систем линейных уравнений c помощью метода Крамера, научить решать системы линейных уравнений, используя метод Крамера.

Развивающая:

Способствовать развитию: логического мышления, памяти, умению сравнивать, обобщать, анализировать, интереса к избранной специальности.

Воспитательная:

Стремиться воспитывать: чувства ответственности, исполнительности, аккуратности, чувство гордости за избранную профессию, положительное отношение к знаниям, учениям, интерес к математике

Межпредметные связи:

История, русский язык, информатика

Обеспечение занятия:

Технические средства обучения: компьютер, проектор с мультимедийным экраном, презентация Power Point.

ПЛАН УРОКА

1.Организационный момент (1 мин.)

Здравствуйте, ребята. Тема урока: «Решение систем линейных уравнений методом Крамера». Ученый-математик Колмогоров А.Н. говорил: «Без знаний математики нельзя понять ни основ современной техники, ни того, как ученые изучают природные и социальные явления», поэтому математика связана с будущей специальностью. В результате изучения темы научимся решать задачи прикладного характера для профессиональной деятельности.

2. Постановка целей занятия (2 мин)

Цели урока: повторить пройденный материал; углубить знания по теме «Решение систем линейных уравнений»; изучить решение систем линейных уравнений с помощью метода Крамера; научиться решать системы двух линейных уравнений с двумя неизвестными и трех линейных уравнений с тремя неизвестными, используя метод Крамера.

3. Проверка домашнего задания (10 мин.)

2 студента около доски вычисляют определитель 2 порядка и определитель 3 порядка (правила треугольника), а остальные занимаются проверкой знания.

4. Проверка знаний

Какое уравнение называется линейным?

Напишите систему m линейных уравнений с n переменными.

Назовите коэффициенты при переменных.

Какие числа называются свободными членами?

Что является решением системы?

Какие методы решения систем линейных уравнений знаете?

Ответы: Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.

5. Изучение нового материала (30 мин.)

В школьном курсе рассматриваются способ подстановки и способ сложения. В курсе высшей математике решают методом Крамера, методом Гаусса и с помощью обратной матрицы. Рассмотрим решение систем линейных уравнений методом Крамера

5.1 Знакомство с биографией Крамера

При изучении новой темы «Решение систем линейных уравнений методом Крамера» важное место занимает связь истории с математикой, что прививает интерес к предмету. Познакомимся с биографией Габриэля Крамера.

Сведения из истории

Крамер является одним из создателей линейной алгебры. Одной из самых известных его работ является «Введение в анализ алгебраических кривых», опубликованный на французском языке в 1750 году. В ней Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера.

Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария) в семье врача.

Уже в детстве он опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики.

В 18 лет он успешно защитил диссертацию. Через 2 года Крамер выставил свою кандидатуру на должность преподавателя в Женевском университете. Учёный много путешествовал по Европе, перенимая опыт у знаменитых математиков своего времени – Иоганна Бернулли и Эйлера в Базеле, Галлея и де Муавра в Лондоне и других. Со многими из них он продолжал переписываться всю жизнь.

В 1729 году Крамер возобновляет преподавательскую работу в Женевском университете. В это время он участвует в конкурсе Парижской Академии и занимает второе место. Талантливый учёный написал множество статей на самые разные темы: геометрия, история, математика, философия. В 1730 году он опубликовал труд по небесной механике.

В 1740-е гг. Иоганн Бернулли поручает Крамеру подготовить к печати сборник своих работ. В 1742 году Крамер публикует сборник в 4-х томах. В 1744 году он выпускает посмертный сборник работ Якоба Бернулли (брата Иоганна Бернулли), а также двухтомник переписки Лейбница с Иоганном Бернулли. Эти работы вызвали большой интерес со стороны учёных всего мира.

Габриэль Крамер скончался 4 января 1752 года во Франции

5.2 Решение системы линейных уравнений методом Крамера

Теорема Крамера.

Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Заменяя столбец с коэффициентами соответствующей переменной свободными членами:

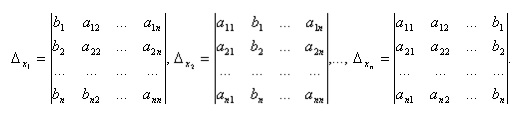
При решении системы уравнений могут встретиться три случая:

1) система линейных уравнений имеет единственное решение

(система совместна и определённа)

Условия:

2) система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

Условия:

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

3) система линейных уравнений решений не имеет

(система несовместна)

Условия:

Система называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.

6. Закрепление. (40 мин)

6.1 Решение системы двух линейных уравнений с двумя неизвестными решаем 3 способами: метод подстановки, сложения и методом Крамера

1)

Решение: Вычислим определитель системы и определителии :

, ,

Найдем значения х и у по формулам Крамера: ;  

Итак, решение системы есть (3; -1)

2)Фирма состоит из двух отделений, суммарная величина прибыли которых в минувшем году составила 12 млн усл. ед. На этот год запланировано увеличение прибыли первого отделения на 70%, второго – на 40%. В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: a) в минувшем году; б) в этом году?

Решение. Пусть x и y – прибыли первого и второго отделений в минувшем году.

Тогда условие задачи можно записать в виде системы:

Решив систему, получим x = 4, y = 8.

Ответ: а) прибыль в минувшем году первого отделения - 4 млн усл. ед., второго - 8 усл.ед.:

б) прибыль в этом году первого отделения 1,7. 4 = 6,8 млн усл. ед.,

второго 1,4. 8 = 11,2 млн усл. ед.

6.2 Решение системы трех линейных уравнений с тремя двумя неизвестными методом Крамера

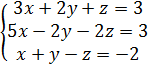
Ответ: (1; -1; 2)

Решение. Вычислим определитель системы и определители при неизвестных:

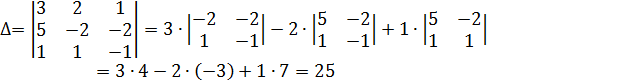
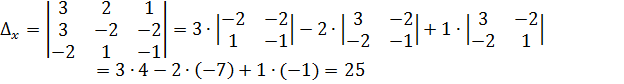
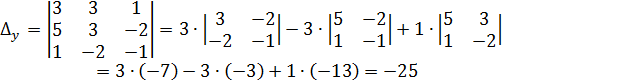
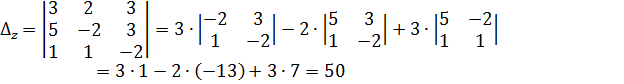
Найдем значения x, y, z по формуле Крамера:

Ответ: (1; -1; 2)

Дополнительно:

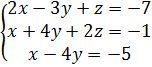
7. Домашнее задание (2мин.)

Решите системы:

1.  

2.   2)

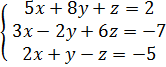
8. Подведение итогов. (5 мин)

1.     Обсуждение с обучающимися достижения цели и задач занятия.

2.     Аргументированное комментирование оценок за пару.

Литература:

Основная

Григорьев В.П., Дубинский Ю.А. Элементы высшей математики. Москва, 2014

Дополнительная

Соловейчик И.Л., Лисичкин В.Т. Сборник задач по математике для техникумов с решениями. М.: ООО «ОНИКС 21  века»; «Мир и Образование», 2003

Скачано с www.znanio.ru