Решение задач с параметрами графическим методом

Конспект урока

Тема занятия: Решение задач с параметрами графическим методом.

Тип занятия: занятие -практикум

Учебная задача занятия: Практиковать решение  задач вида  и  координатно-параметрическим методом и задач вида  графическим методом.

Диагностируемые цели занятия:

В результате занятия ученик

знает:

- определение: КП-плоскости, КП-метода решений задач с параметрами, МЧО на КП-плоскости, функционально-графического способа;

- алгоритм решения: неравенств МЧО на КП-плоскости, систем уравнений/неравенств;

- формулировки теорем для уравнений вида  и ;

- формулировки теорем по функционально-графическому методу;

- правила преобразования графиков элементарных функций (параллельный перенос, сжатие/растяжение, симметрия);

- таблицу равносильных переходов в методе декомпозиции;

умеет:

- решать задачи вида  и  координатно-параметрическим методом (в частности методом частичных областей для неравенств и их систем);

- решать задачи вида  графическим методом, где  обозначает .

- решать системы уравнений/неравенств, где одно или оба из уравнений/неравенств с параметром;

- преобразовывать графики функций, изображать их на плоскости ;

- осуществлять равносильные переходы с помощью метода декомпозиции.

понимает:

- что рациональнее применить: аналитический или графический метод,  КП-метод или функционально-графический, если выбрали графический метод решения задач с параметрами.

Учебные действия, формируемые на уроке:

•        Личностные: умение учащегося устанавливать связи между целью учебной деятельности и её мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом, должна осуществляться осмысленная организация собственной деятельности ученика.

•        Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что ещё неизвестно; планирование - определение последовательности промежуточных целей с учётом конечного результата; оценка - выделение и осознание учащимся того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения; волевая саморегуляция как способность к мобилизации сил и энергии,  способность к волевому усилию к выбору в ситуации мотивационного конфликта и  к преодолению препятствий.

•        Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т. е. определение цели сотрудничества, функций участников, способов взаимодействия, в том числе совершенствование навыков работы в группе, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение.

•        Познавательные: анализ объектов с целью выделения признаков (существенных, несущественных); построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей, структурирование знаний, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.

Методы обучения: репродуктивный, частично-поисковый.

Форма работы: парная.

Средства обучения: традиционные, презентация.

Структура занятия:

•        Мотивационно-ориентировочная часть (5 минут).

- Актуализация знаний.

- Мотивация.

- Постановка учебной задачи (цели) урока.

•        Операционно-познавательная часть (38 минуты).

•        Рефлексивно-оценочная часть (2 минуты).

Ход занятия:

Мотивационно – ориентировочная часть.

Актуализация знаний.

- Дайте определение КП-метода.

- (Метод решения задач с параметрами, использующий КП-плоскость. А КП-плоскость – это плоскость, в которой одна ось () – координатная, другая – () параметрическая.)

- Когда удобно использовать КП-метод.

- (Когда координата  является функцией параметра :  или когда параметр а является функцией координаты : )

- Каким методом решается неравенство на КП-плоскости?

- (Методом частичных областей)

- Назовите алгоритм МЧО на основе КП-метода.

- (1. Найдем на КП-плоскости ОДЗ

2. Построим на КП-плоскости линии, состоящие из всех точек, при значениях координаты  и параметра  каждой из которых выражение обращается в нуль или не существует, и разобьем этими линиями найденную ОДЗ на «частичные области».

3. Исследуем знак выражения в каждой из по­лученных «частичных областей».

- Назовите равносильные переходы из метода декомпозиции для выражения .

-()

- Для выражения ?

- ()

- Как построить график функции ?

- (Построить график функции . Зеркально от­разить данный график относительно оси ординат)

- Какие преобразования графиков используются в функционально-графическом методе?

- (Параллельный перенос, растяжение/сжатие, симметрия).

Мотивация.

На прошлых занятиях вы изучили графические способы решения задач с параметрами, а именно КП-метод и функционально-графический метод.

Постановка учебной задачи (цели) занятия.

Поэтому сегодня мы повторим изученный материал и подготовимся к контрольной работе, которая будет на следующем занятии.

Операционно-познавательная часть.

Все задачи решаются в парах, проверка происходит с эталона со слайдов презентации.

Задача №1. Определить количество корней уравнения  в зависимости от значений параметра .

Решение:

Для начала упростим исходное выражение до вида, т.е. чтобы параметр а являлся функцией координаты .

Данное уравнение равносильно совокупности четырех систем:

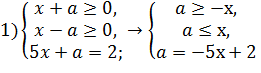
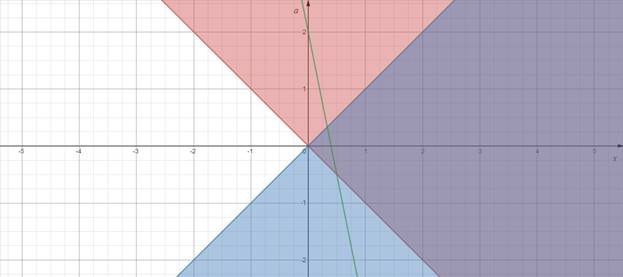
Рисунок 1

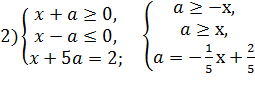
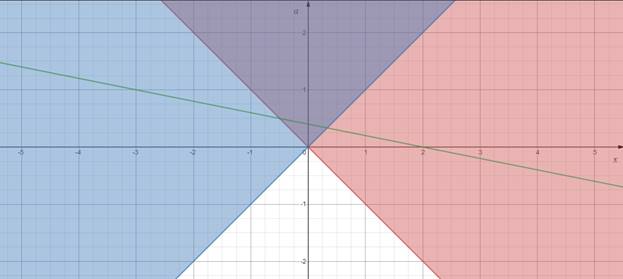
Рисунок 2

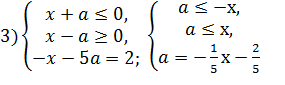
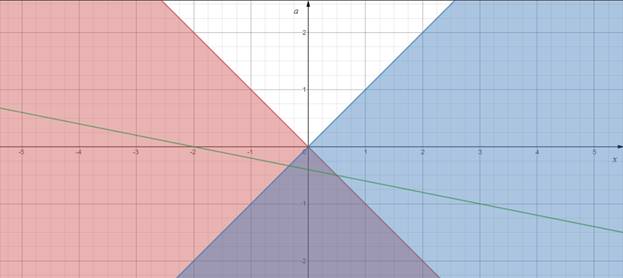
Рисунок 3

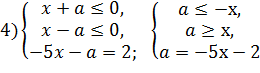
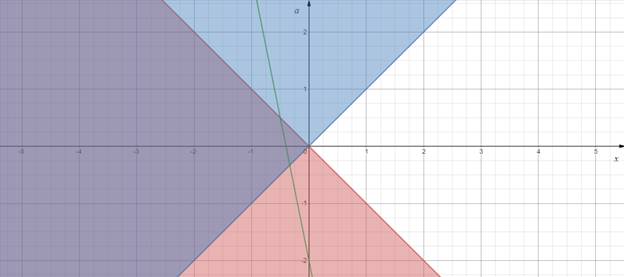
Рисунок 4

Т.к. в каждом случае , то можно рассматривать КП-плоскость  с вертикальной параметрической осью .

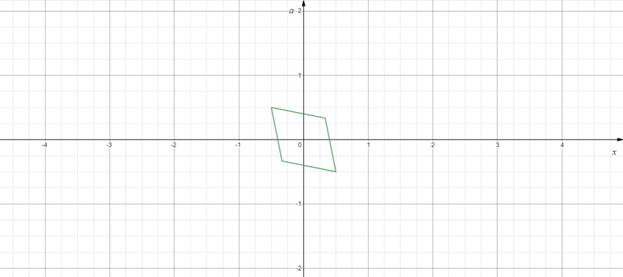
Рисунок 5

Найдем координаты вершин параллелограмма, для этого решим системы, составленные из уравнений прямых линий, получим .

Рассматривая прямые  в пе­ресечении с параллелограммом, получаем ответ.

Ответ: при  или  нет корней; при  один корень; при  два корня.

Задача №2. Найти при каких значениях параметра  система неравенств 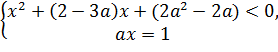  имеет решение.

Решение: будем действовать по алгоритму

1. ОДЗ:

2.

Выразим координату  через функцию параметра :

Изобразим данные линии на КП-плоскости с горизонтальной параметриче­ской осью , т.к. .

3. Исследуем знак выражения в каждой из по­лученных «частичных областей».

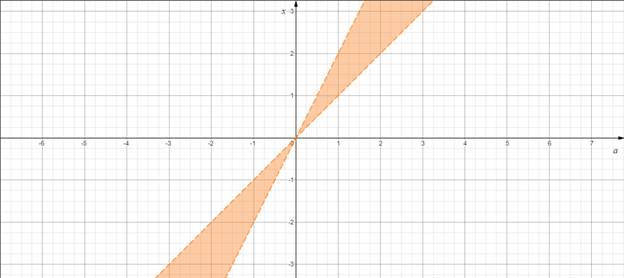
Рисунок 6

 – гипербола

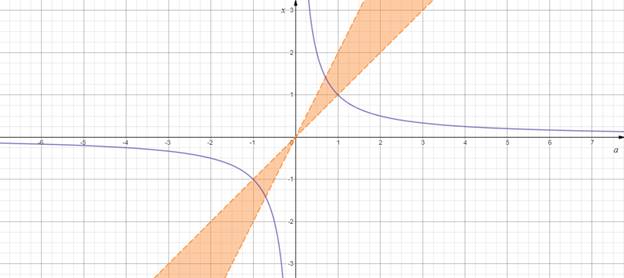
Рисунок 7

Найдем общее решение системы, для этого найдем точки пересечения гиперболы  с прямыми :

 .

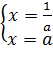
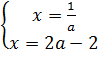
«Считывая» информацию с графика, видим, что система имеет решения при .

Ответ: .

Задача №3. При каких значениях параметра  система 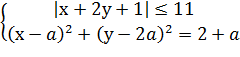   имеет единственное решение.

Решение:

Пусть

- область между данными прямыми.

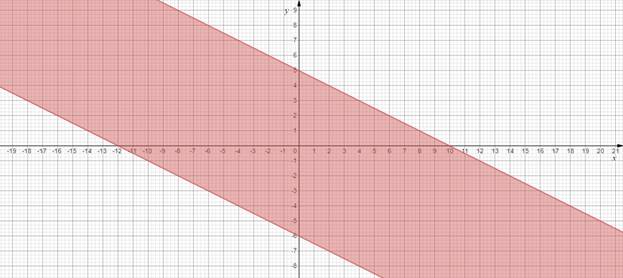
Рисунок 8

 - окружность с центром ) и ,  Центр окружности лежит на прямой .

Окружность не может располагаться между прямыми, т.к. в этом случае будет бесконечно много решений.

Рассмотрим случаи касания, когда окружность лежит вне закрашенной области.

I. Найдем точку пересечения прямых  и .

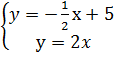
. подставим координаты этой точки в уравнение окружности:
-не удовлетворяет условию, т.к. , иначе центр попадет внутрь закрашенной области.

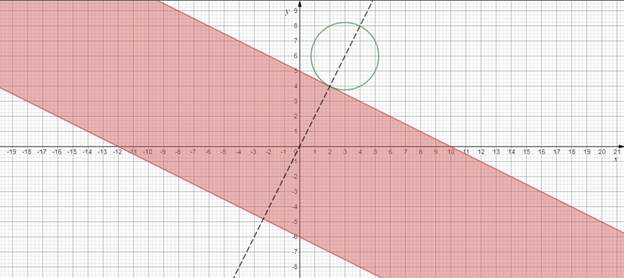
Рисунок 9

II. Рассмотрим . График  - точка с координатами , подставим в - верно, следовательно  – решение.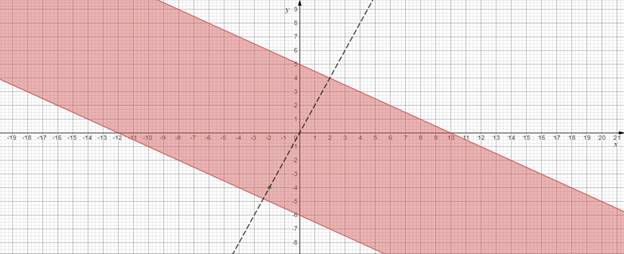

Рисунок 10

Ответ: .

Задача №4. Для каждого допустимого значения параметра решить неравенство .

Решение: будем действовать по алгоритму

1. ОДЗ:

2.

Выразим параметр через функцию координаты , используя равносильный переход метода декомпозиции:

Линии .

Изобразим данные линии на КП-плоскости  с вертикальной параметрической осью , т.к. .

3. Исследуем знак выражения в каждой из по­лученных «частичных областей».

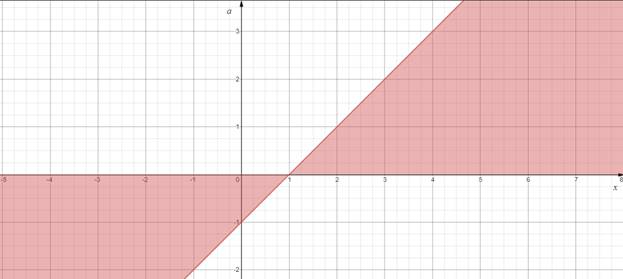
Рисунок 11

Найдем общее решение, с учетом области определения функции:

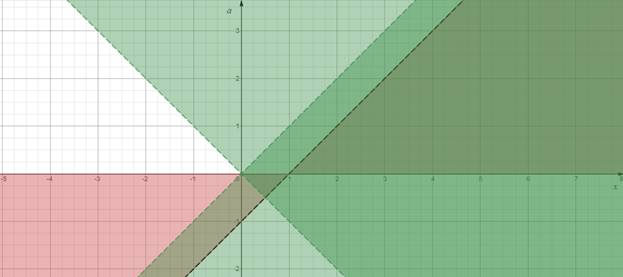
Рисунок 12

«Считывая» информацию с графика, получаем:

при ;

при ;

при ;

при .

Ответ: при ; при ; при ; при .

Рефлексивно-оценочная часть.

-Какова была цель урока?

- (Практиковать решение задач с параметрами графическим методом)

- Достигли мы её?

- (Да)

- Как мы её достигли?

-(Решали задачи вида  и  координатно-параметрическим методом и задачи вида  функционально-графическим методом)

Домашнее задание.

1. Найти при каком значении параметра  уравнение   имеет решения, и все решения принадлежат отрезку .

Ответ:

2. Найти при каких значениях параметра  система неравенств 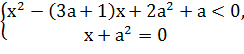  имеет решения.

Ответ:

3. При каких значениях параметра  система 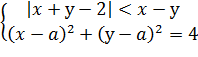    имеет решение.

Ответ:

4. Для каждого значения параметра решить неравенство .

Ответ: при ;  при ; при ; при ; при .

Скачано с www.znanio.ru