Свойства и график функции у = sin x

Филиал бюджетного профессионального образовательного учреждения Чувашской Республики

«Чебоксарский медицинский колледж»

Министерства здравоохранения Чувашской Республики в городе Канаш

 

РАССМОТРЕНО и ОДОБРЕНО  на заседании  ЦМК ОГСЭ дисциплин Протокол № ____       от «___» ___________ 20 ___ г. Председатель ___________ Л.М. Иванова

 

 

 

 

 

 

 

 

 

Свойства и график функции у =sin x, y = cos x

специальность 34.02.01 Сестринское дело (базовая подготовка)

учебная дисциплина БД.04 Математика

 

 

 

 

 

 

 

 

 

              

Составил: Семенова А.М., преподаватель математики филиала БПОУ «Чебоксарский медицинский колледж» Министерства здравоохранения Чувашии в г Канаш

                 

 

 

 

Канаш, 2020

 

 

 

Л1. Сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики;

Л2. Понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;

Л8. Отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;

• метапредметных:

М1. Умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;

М5. Владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;

М7. Целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;

• предметных:

П1. Сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;

П2. Сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

П5. Сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;

 

 

 

 

 

 

 

 

Ход уроков

I. Сообщение темы и целей уроков

 II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Упростите выражение:

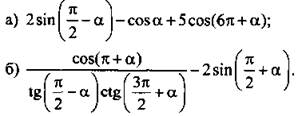
Вариант 2

1. Упростите выражение:

 

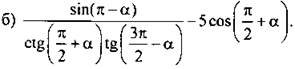
III. Изучение нового материала

Из ранее изученного нам известны многие свойства двух основных тригонометрических функций - синуса и косинуса. Рассмотрим графики этих функций и на их основе детализируем такие свойства.

1. Функция y = sin x, ее свойства и график

Обсудим построение графиков функций синуса и косинуса. Сначала построим график функции синуса на отрезке [0; 2π]. Отметим на оси ординат точки (0; -1) и (0; 1), на оси абсцисс - точку (2π; 0). Разделим отрезок [0; 2π] и единичную окружность на 8 равных частей (учтите, что длина отрезка [0; 2π] равна 2π ≈ 6,28). Каждая такая часть равна π/4. Для построения точки графика с абсциссой t используем определение синуса. Отметим точку Рt на единичной окружности и проведем через Рt прямую, параллельную оси абсцисс. Точка пересечения этой прямой и прямой х = t искомая, так как ее ордината совпадает с ординатой точки Рt и по определению sin t равен ординате точки Рt.

 

 

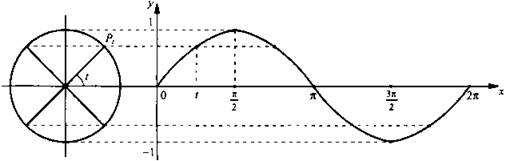
На рисунке приведено построение восьми точек графика. Соединяя их плавной кривой, получаем эскиз графика синуса на отрезке [0; 2π]. Для построения графика функции вне этого отрезка учтем периодичность функции синуса, т. е. sin (х + 2πn) = sin х (где n - произвольное целое число). Поэтому во всех точках х0 + 2пn (где 0 < x0 < 2π) значения синуса совпадают. Следовательно, график синуса на всей прямой получается из построенного графика с помощью параллельных переносов его вдоль оси абсцисс (вправо и влево) на 2π, 4π, 6π и т. д. График функции синуса называется синусоидой. Отрезок [-1; 1] оси ординат, с помощью которого находили значения синуса, иногда называют линией синусов.

 

 

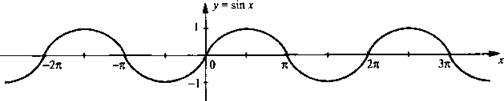
Используя построенный график, приведем основные свойства функции у = sin х:

1. Область определения D(y) = (-∞; +∞).

2. Функция нечетная (т. е. у(-x) = -e(x))> и ее график симметричен относительно начала координат.

3. Функция возрастает на отрезках вида  и убывает на отрезках вида  где k ∈ Z.

4. Функция ограничена, т. е. -1 ≤ у(х) ≤ 1.

5. Наименьшее значение функции yнаим = -1 (достигается в точках вида ) и наибольшее значение унаиб = 1 (достигается в точках вида ).

6. Функция непрерывная.

7. Область значений Е(у) = [-1; 1].

8. Функция периодическая с наименьшим положительным периодом Т = 2п, т. е. у(х + 2пk) = y(x).

Рассмотрим некоторые примеры.

Пример 1

Найдем наименьшее и наибольшее значения функции: 

а) В силу ограниченности функции у = sin х имеем неравенство -1 ≤ sin x ≤ 1. Умножим все части этого неравенства на положительное число 3 и получим неравенство того же знака -3 ≤ 3sin x ≤ 3. Вычтем их всех частей число 1: -4 ≤ 3sin х - 1 ≤ 2. Таким образом,yнаим = -4 и yнаиб = 2.

б) Используем основное тригонометрическое тождество (1) и в данной функции перейдем к величине sin х. Получим:  Введем вспомогательную величину z = sin х, причем -1 ≤ z ≤ 1. Тогда необходимо найти наибольшее и наименьшее значения квадратичной функции  на отрезке [-1; 1].

 

 

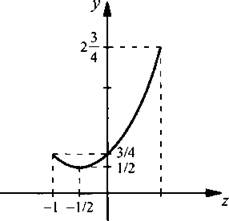
Графиком этой функции является парабола, направленная ветвями вверх (см. рисунок), вершина которой имеет координаты zB = -1/2 и  В этой точке функция имеет наименьшее значение. Наибольшее значение функция имеет в точке z = 1, и оно равно  Итак, получили:  Поэтому 

 

 

 

Пример 2

Построим график функции 

Такой график получается из графика функции у = х смещением на π/6 влево вдоль оси абсцисс и растяжением в 2 раза вдоль оси ординат.

 

 

.

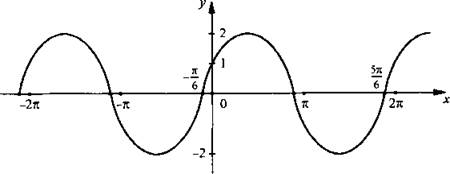
2. Функция у = cos x, ее свойства и график

Для построения графика функции косинуса учтем формулу приведения  Поэтому значение косинуса в любой точке x0 равно значению синуса в точке  Тогда график косинуса получается из графика синуса с помощью параллельного переноса на единиц влево вдоль оси абсцисс. Поэтому график функции у = cos х также является синусоидой.

 

 

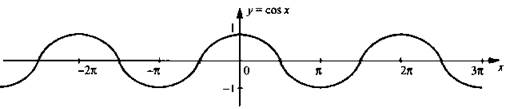
Перечислим основные свойства функции у = cos x:

1. Область определения D(y) = (-∞; +∞).

2. Функция четная (т. е. y(-х) = y(х)), и ее график симметричен относительно оси ординат.

3. Функция возрастает на отрезках вида [-π + 2πk; 2πk] и убывает на отрезках вида [2πk; π + 2πk], где k ∈ Z.

4. Функция ограничена, т. е. -1 ≤ y(х) ≤ 1.

5. Наименьшее значение функции унаим = -1 (достигается в точках вида х = π + 2пk) и наибольшее значение унаиб = 1 (достигается в точках вида х = 2пk).

6. Функция непрерывная.

7. Область значений Е(у) = [-1; 1].

8. Функция периодическая с наименьшим положительным периодом Т= 2п, т. е. у(х + 2пk) = у(х).

Рассмотрим наиболее типичные примеры.

 

3. Периодичность функций у = sin х, у = cos x

Перейдем к следующему свойству функции - периодичности. Многие реальные явления и процессы имеют повторяющийся (периодический) характер. Например, минутная стрелка занимает одинаковое положение на циферблате часов через каждый час. Такого типа процессы называют периодическими, как и их функции.

Функция f(х) называется периодической с периодом Т (Т - некоторое действительное число, отличное от нуля), если:

1) для любого х из области определения функции значение аргумента х ± Т также принадлежит области определения функции;

2) выполняется равенство f(x + T) = f(x) = f(x - Т). Обычно под периодом функции понимают наименьший из всех положительных периодов (основной период функции).

 

 

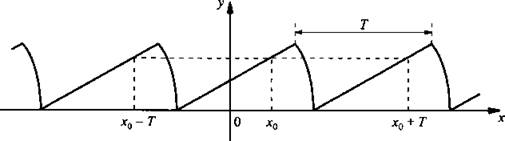
Исходя из определения тригонометрических функций, нетрудно установить, что период функций sin x и cos х составляет 2π, период функций tg х и ctg х - π. Действительно, функции синуса и косинуса определены на всей числовой оси, sin (х + 2π) = sin х и cos (x+ 2π) = cos х для любого х. Аналогично области определения функций тангенса и котангенса включают как точку х, так и точки х ± π. При этом выполняются равенства tg(х + π) = tg х и ctg (х + π) = ctg x.

 

Пример 8

Докажем, что если функция f(х) периодическая с периодом Т, то при любом целом n ≠ 0 число nТ также период этой функции.

Пусть для определенностиn п = 4. Тогда нужно доказать, что число 4Т является также периодом функции f(х). Найдем  Итак, было показано, что для любого х выполнено равенство f(x + 4T) = f(x). Поэтому по определению число 4Т является также периодом функции f(х).

 

IV. Контрольные вопросы

1. Основные свойства и график функции у = sin х.

2. Свойства функции у = cos x и ее график.

3. Как получить график функции у = cos x, используя график функции у = sin x?

4. Определение периодической функции.

5. Основной период функции.

6. Основной период функций  и 

7. Основной период функций  и 

 

 

V. Задание на уроках

§ 40, № 712 (1, 3); 713 (1, 3); § 41, № 723 (а); 723-724 (а, б);

VI. Задание на дом

§ 40, № 712 (2, 4); 713 (2,4); § 41, № 723 (2,4); 723-724 (2,4);

 

VII. Творческое задание

Постройте график функции, уравнения или неравенства:

 

VIII. Подведение итогов уроков