Свойства степени с натуральным показателем

Школа: МОУ «Школа №18 города Тореза»

Учитель: Фомина Надежда Валентиновна

Предмет: алгебра                                                              

Класс: 7 класс

Тема: Свойства степени с натуральным показателем

Цель:

1) открыть свойства степени с натуральными показателями, сформировать умение применять эти свойства для вычислений;

2) повторить и закрепить: определение степени с натуральным показателем.

Тип урока: урок открытия новых знаний

Формируемые УУД:

Предметные:

·        знает свойства умножения и деления степеней с одинаковым основанием;

·        применяет свойства для вычисления значений выражений, упрощения буквенных выражений;

·        применяет определение степени.

Метапредметные:

·        планирует свои действия в соответствии с решаемой задачей;

·        использует речь для регуляции своих действий;

·        осуществляет итоговый и пошаговый контроль по эталону;

·         оценивает свои достижения, осознает трудности, ищет их причины и пути преодоления.

·        осуществляет поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы;

·        строит речевые высказывания в устной и письменной форме;

·        проводит сравнение и классификацию по заданным критериям;

·        формулирует собственное мнение и позицию;

·        осуществляет взаимный контроль и оказывает в сотрудничестве необходимую взаимопомощь;

·         адекватно использует речевые средства для эффективного решения разнообразных коммуникативных задач.

Личностные:

·         положительно относится к учению;

·        проявляет активность, самостоятельность;

·         имеет учебно-познавательный интерес, желание приобретать новые знания, умения, совершенствовать имеющиеся;

·        ориентирован на осознание своих удач и неудач, трудностей, стремление преодолевать возникающие затруднения.

Оборудование: раздаточный материал, эталоны, проектор, презентация .

Краткая аннотация к работе: Урок открытия новых знаний, построен в соответствии с технологией системно- деятельностного метода.

 

Ход урока:

 

Этап 1. Мотивация к учебной деятельности.

Цель этапа:

1) включить учащихся в учебную деятельность;

2) определить содержательные рамки урока.

Организация учебного процесса на этапе 1:

– Здравствуйте, ребята!  Сегодня мы продолжим путешествие в увлекательный мир степеней, одночленов и многочленов. Вместе с нами этот путь пройдёт Алиса – героиня произведений Льюиса Кэролла «Алиса в стране чудес» и «Алиса в Зазеркалье». Почему именно Алиса? Мне кажется, что многие  цитаты из этих сказок  подходят к сегодняшнему уроку.

«- Не грусти, - сказала Алисa. - Рано или поздно все станет понятно, все станет на свои места и выстроится в единую красивую схему, как кружева. Станет понятно, зачем все было нужно, потому что все будет правильно».

-Мы тоже находимся с вами в начале изучения темы «Многочлены», но постепенно наши знания будут выстраиваться в красивую схему, похожую на математические кружева.

(Приложение 1. Слайд 2).

     На прошлом уроке мы узнали, что такое степень с натуральным показателем. Сегодня мы узнаем новое о степенях.

 

Этап 2. Актуализация знаний и фиксация затруднения в пробном учебном действии.

Цель этапа:

1) организовать актуализацию изученных способов действий, достаточных для построения нового знания;

2) зафиксировать актуализированные способы действий в речи;

3) зафиксировать актуализированные способы действий в знаках (эталоны);

4) организовать актуализацию мыслительных операций, достаточных для построения нового знания: анализ, аналогия, обобщение;

5) мотивировать к выполнению пробного действия;

6) организовать самостоятельное выполнение пробного учебного действия;

7) организовать фиксацию индивидуальных затруднений в выполнении учащимися пробного учебного действия или в его обосновании.

Организация учебного процесса на этапе 2:

- Что называется степенью числа а с натуральным показателем n? (Степенью числа а с натуральным показателем n называется произведение, состоящее из n множителей, каждый из которых равен а).

- Прочитайте выражение 6⁷.Назовите основание и показатель степени.

Учащиеся пишут математический диктант. (Два ученика работают за доской.)

1) Запишите  произведение а· а· а · а в виде степени?

2) Запишите выражение 6·6·6·6·6·6·6 в виде степени? Подчеркните одной чертой основание, двумя показатель степени.

3) Чему равна первая степень числа -5?

4) Вычислите: (-0,1)².

5) Выпишите степени, значения, которых положительные : (-7)⁴; (-11)⁵; (-1)⁰.

6) Сравните : -2⁶ и (-2)⁶.

7) Вычислите значение степени, если основание равно 3, показатель равен 4.

8) Найти значение выражения 11⁹:11⁷

Доски открываются,  и ученики проверяют свою работу, сверяясь с ответами  на доске. По результатам разминки  в листе достижений (Приложение 2) делается отметка.

-Кто верно выполнил задание 1-7 ? Какие ошибки были допущены?

-Кто выполнил задание 8? В чём причина затруднения?

3. Выявление места и причины затруднения.

Цель этапа:

1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности.

Организация учебного процесса на этапе 3 :

 «Мало кто находит выход, некоторые не видят его, даже если найдут, а многие даже не ищут».

(Приложение 1. Слайд 3).

 -Какое задание вы должны были выполнить?  (Найти значение выражения).

-В каком месте возникло затруднение? (Я не смог найти значение выражения, так как нужно было выполнять громоздкие вычисления).

-А почему оно возникло? (Вероятно, есть какие-то способы преобразования выражений со степенями, но я их не знаю).

4. Построение проекта выхода из затруднения

Цель этапа:

1) организовать коммуникативное групповое взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;

2) согласовать цель и тему урока.

Организация учебного процесса на этапе 4:

 «План, что и говорить, был превосходный: простой и ясный, лучше не придумать. Недостаток у него был только один: было совершенно неизвестно, как привести его в исполнение».

(Приложение 1. Слайд 4).

- Какую цель вы перед собой поставите?  (Узнать свойства степеней с натуральными показателями).

-Сформулируйте тему нашего сегодняшнего урока (Свойства степеней с натуральными показателями).

-Как мы будем достигать поставленной цели, как узнаем свойства степеней? (Можно найти соответствующий материал в учебнике, справочнике, материал может объяснить учитель; можем вывести свойства самостоятельно, используя уже известные алгоритмы, правила и свойства).

- Как можно назвать свойство степеней, с помощью которого можно решить пример 8? (Деление степеней).

-Что общего у этих степеней? ( Основания.  Деление степеней с одинаковыми основаниями).

- Как вы думаете, могут ли быть другие свойства степеней? Какие? (Умножение степеней с одинаковыми основаниями.)

- Итак, мы должны сформулировать и доказать два свойства степеней с натуральными показателями:

1. Умножение степеней с одинаковыми основаниями: .

2. Деление степеней с одинаковыми основаниями: .

План действий:

1.     Записать несколько примеров для соответствующего свойства.

2.     Выполнить действия, применяя определение степени .

3.     Увидеть закономерность. Сделать вывод.

4.     Записать свойство в буквенной форме.

5.     Доказать свойство. (Приложение 1. Слайд 5).

 

5. Реализация построенного проекта.

«Думай о смысле, а слова придут сами».
Цель этапа:

1) Сформулировать и доказать свойства степеней с натуральными показателями.

2) Зафиксировать свойства в виде формул и создать эталон.

Организация учебного процесса на этапе 5:

- Данную работу предлагаю выполнить в группах. Класс разбивается на группы. Каждая из них получает одно из заданий 1или 2.

·        Идёт работа в группах по предложенному плану. Учащиеся записывают в тетрадях примеры на соответствующее свойство , вычисляют значения, пользуясь определением степени.

·        Находят закономерность. Формулируют правило.

·        Доказывают свойство на больших листах.

·        Учащиеся подводят итоги в группах, фиксируют результаты. Представляют у доски результаты  работы в виде формул и эталона. Проводят доказательство.

- Вы достигли поставленной цели? (Да. Мы сформулировали и доказали свойства степеней с натуральными показателями).

-  Какие задания вы теперь можете выполнять? (Мы теперь сможем выполнять умножение, деление степеней с одинаковыми основаниями).

- Объединим эти правила под названием «Свойства степеней с натуральными основаниями». Сверим полученные правила умножения и деления степеней с учебником.

(Приложение 1. Слайд 6).

1. При умножении степеней с одинаковыми основаниями основание остаётся тем же, а показатели складываются:   2. При делении степеней с одинаковыми основаниями основание остаётся тем же, а из показателя делимого вычитается показатель делителя:

- Почему в правиле  деления степеней записаны требования ? ( , так как тогда показатель частного будет натуральным числом, а  .

-Что теперь вы должны сделать? (Мы должны научиться применять свойства.)

 

       6. Первичное закрепление во внешней речи.

Цель этапа:

Научиться применять свойства степеней в типовых заданиях.

Организация учебного процесса на этапе 6:

«Все, что сказано три раза, становится истиной».

 (Приложение 1. Слайд 7).

-Чему равно значение выражения: 11⁹:11⁷? ( 11⁹:11⁷=11^9-7=11²=121).

- Учащиеся решают №№ 403, 404, 408, 415, 416 (а, б) у доски с объяснением, проговаривая правила умножения и деления степеней с одинаковым основанием.

- Ну а теперь, давайте разомнемся!  (Двигательная разминка- элемент сингапурской технологии. С помощью этого задания у детей развивается социальный навык, развивается речь. Ученики осуществляют повторение и закрепление новых знаний. Происходит смена вида  деятельности. Учитель должен подготовить вопросы на карточках.Это примеры на умножение и деление степеней с одинаковыми основаниями. У каждого ученика должна быть карточка. Оформление листочков: листок согнут вдвое, снаружи  написан пример, а внутри его решение. Ученик, получая пример, решает его устно и сверяет его с тем, что написано на внутренней стороне листа. Работает схема: опроси- опроси- обменяйся карточкой ).

-  Возьмите листочки с примером. Посмотрите задание, дайте ответ, проверьте себя. Спрячьте ответ. По моей команде встаньте, задвиньте стулья и найдите себе пару! В паре начинает отвечать тот, кто выше ростом. Задайте друг другу вопросы, расскажите правило действия со степенями, которое вы применили в примере, получите ответ,  поменяйтесь карточками и найдите себе новую пару. Не забудьте поприветствовать партнера и поблагодарить его. На выполнение задания вам дается  4 мин. Итак, начинаем. Встаньте и задвиньте стулья. Найдите себе пару. ( Свою работу в парах  ученики оценивают в листе достижений).

 

7.Самостоятельная работа с самопроверкой по эталону.

Цель этапа:

проверить своё умение применять новое свойство в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки, обучение навыкам самоконтроля.

 « – Что ты хочешь?
– Я хочу убить время.
–  Время очень не любит, когда его убивают».

(Приложение 1. Слайд 8).

− Мы с вами , ребята, вовсе не убиваем время, а проводим его с пользой для себя.  Теперь, когда у нас появилось новое знание, что  необходимо сделать? (Надо проверить, правильно ли поняли  как применяются  изученные свойства степени.)

·        Учащиеся выполняют самостоятельную работу.

·        Осуществляют самопроверку по эталону. (Приложение 1 Слайд 9).

− У кого задание вызвало затруднение?

− В каком месте возникло затруднение?

− Кто может сказать, что правильно понял, как применять свойства степеней?

− Кому еще надо учиться?

 

8. Включение в систему знаний и повторение.

Цель этапа:

1) тренировать навыки использования нового алгоритма при выполнении деления рациональных чисел;

2) повторить правила действий с рациональными числами.

«Нужно бежать со всех ног , чтобы только оставаться на месте, а чтобы куда-то попасть, надо бежать как минимум вдвое быстрее !»

 (Приложение 1. Слайд 10).

 

-Теперь вам нужно быстро воспользоваться шансом и получить «5».  Объявляется аукцион «Получи пятерку»!  Пять  получит тот ученик, кто назовет  математиков, написавших известные сказки. (Учитель считает до трех , как на аукционе,   и объявляет его результат.)

-Следующей игрой будет  «Математическое лото» . Его  следует выполнять в парах. Схема простая: решаю- ищу ответ- вставляю буквы- получаю два слова. Удачи!

(Приложение 3, Приложение 1. Слайд 11 ).

 

 

МАТЕМАТИЧЕСКОЕ ЛОТО

 

81

-1

0

4

-16

 

32

25

1

9

10000

0,001

0,04

 

 

ЛЬЮИС КЭРРОЛЛ
Настоящее имя Чарльз Лютвидж До́джсон английский  писатель, математик, логик, философ и фотограф. Автор произведений «Алиса в стране Чудес» и «Алиса в Зазеркалье» (Приложение 1 Слайд  12).

- Сделайте отметку о результатах  «Математического лото» в листе достижений  ( по количеству отгаданных букв 11-12-«5», 10-8- «4», 7-5- «3»)

9. Рефлексия деятельности на уроке

Цель этапа:

1) зафиксировать новое содержание, изученное на уроке;

2) оценить собственную деятельность на уроке;

3) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;

4) обсудить и записать домашнее задание.

 «– А что это за звуки, вон там? – спросила Алиса, кивнув на весьма укромные заросли какой-то симпатичной растительности на краю сада.
– А это чудеса, – равнодушно пояснил Чеширский Кот.
– И… И что же они там делают? – поинтересовалась девочка, неминуемо краснея.
– Как и положено, – Кот зевнул. – Случаются…»

(Приложение 1. Слайд 13).

– Я думаю, что с нами на уроке сегодня тоже случилось чудо: мы сами  открывали новые знания! Давайте назовем,  какие?

-Что использовалось при выведении новых свойств?

– Какие знания нам помогли в работе?

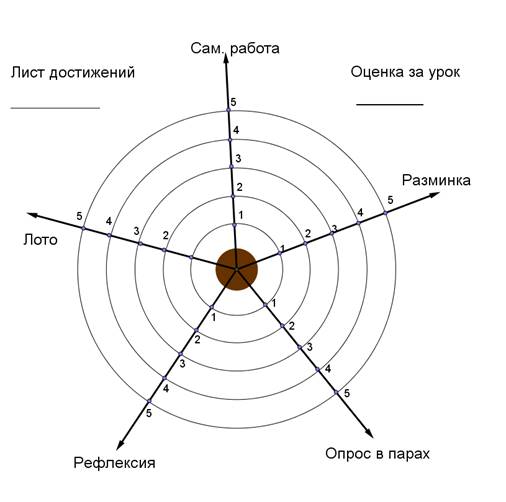
– Оцените свою работу на уроке. В листе достижений станьте на луч «Рефлексия» . В случае , если ваш ответ «Да», делайте шаг на деление по лучу, если ответ «Нет», оставайтесь на месте.

1.        Я понял/ла, какие существуют свойства степеней  с натуральным основанием.

2.        Я понял, как умножать, делить степени с одинаковыми основаниями.

3.        Я научился применять свойства при преобразовании выражений.

4.        Данная тема не вызвала у меня затруднений.

5.        Я смогу самостоятельно выполнить домашнее задание.

 

Домашнее задание:

•      П. 19. Выучить правила

•      №403, №415 (для тех, кто допустил ошибки в самостоятельной работе),

•      №418, №419 (для тех,  кто решил самостоятельную работу без ошибок)

•      Выясните,  кто из советских математиков написал  известную вам сказку?

 (Приложение 1. Слайд 14).

«– Серьезное отношение к чему бы то ни было в этом мире является роковой ошибкой.
– А жизнь – это серьезно?
– О да, жизнь – это серьезно! Но не очень…»

-Спасибо за урок, ребята! Удачного дня!

Приложение2