Технологическая карта Простейшие тригонометрические уравнения.

Технологическая карта (план) занятия № 13

содержание занятия

Конспект  № 13

Тема: Простейшие тригонометрические уравнения.

Ход занятия

1. Организационный момент

Перед началом урока преподаватель проводит проверку подготовленности кабинета к занятию.

- Великий русский писатель Л.Н. Толстой сказал: «Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью».  Это будет эпиграф нашего урока.

- Как вы понимаете это выражение? (Мы должны убедиться, что получить знание можно только через усилия мысли)

2. Мотивационный момент

-Какой раздел математики мы с вами изучаем в настоящий момент? (тригонометрия)

-Какое выражение записано на доске?   2х+4=6    (простейшее уравнение)

- Как вы думаете,  что предстоит нам с вами сегодня на уроке изучить? (решать простейшие тригонометрические уравнения)

- Итак, тема нашего урока «Простейшие тригонометрические уравнения» (слайд 1)

- Цели урока, которые мы с вами должны достичь:

1. познакомиться с понятием простейшие тригонометрические уравнения

2. научиться решать простейшие тригонометрические уравнения.

3. Актуализация опорных знаний

3.1. Устный опрос

¾    Дайте определение синуса угла в единичной окружности.

¾    Дайте определение арксинуса числа.

¾    Какими функция ми являются между собой функции синуса и арксинуса?

¾    Дайте определение косинуса угла в единичной окружности.

¾    Дайте определение арккосинуса числа.

¾    Дайте определение тангенса острого угла.

¾    Дайте определение арккотангенса числа.

¾    Дайте определение котангенса острого угла.

¾    Назовите функцию обратную котангенсу.

¾     Как связаны между собой тангенс и котангенс.

4. Изучение нового материала 

4.1. Уравнение Cos x = a

Определение Простейшие тригонометрические уравнения – уравнения вида Sinx = a, Cosx = a,

tgx = a, ctgx = a.

Решить простейшее тригонометрическое уравнение – значит найти множество всех значений аргумента, при котором данная тригонометрическая функция принимает значение а.

Рассмотрим решения данных уравнений.

Уравнение Cos x = a

Из определения косинуса следует, что . Поэтому если , то уравнение cos x = a не имеет корней. Например, уравнение cos x = - 1,5 не имеет корней.

Решим уравнение cos x = ½. Для решения данного уравнения вспомним, как вычисляется арккосинус числа.

Примеры.  arсcos = , так как cos =  и 0 ≤  ≤

    arсcos = , так как cos =  и 0 ≤  ≤

Для решения уравнения cos x = a необходимо воспользоваться следующей схемой.

-Решим уравнение cos x = ½.

Так как  < 1, то воспользуемся следующей формулой 

х = ± arccos а + 2πn, n є Z. 

х = ± arccos 1/2 + 2πn, n є Z 

х = ±  + 2πn, n є Z  - решение уравнения.

- Решить уравнение cos x = 5.

Так как  > 1, то уравнение не имеет решений.

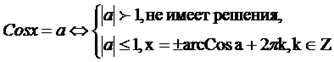
Рассмотрим ещё несколько случаев решения данного уравнения, при решении которых используется единичная окружность.

4.2. Уравнение Sinx = a

Из определения синуса  следует, что . Поэтому если , то уравнение sin x = a не имеет корней. Например, уравнение sin x = 2 не имеет корней.

Решим уравнение sin x = ½. Для решения данного вспомним, как вычисляется арксинус числа.

Примеры.  arсsin = , так как sin  =  и   ≤   ≤

       arсsin = - , так как sin (-) =  и   ≤   ≤ .

Для решения уравнения sin x = a необходимо воспользоваться следующей схемой. (приложение 3)

- Решим уравнение sin x = ½.

Так как  < 1, то воспользуемся следующей формулой 

х = (-1)ⁿ arcsin a + πn, nе Z

х = (-1)ⁿ arcsin ½ + πn, nе Z

х = (-1)ⁿ  + πn, nе Z - решение уравнения.

- Решить уравнение sin x = - 2.

Так как  > 1, то уравнение не имеет решений.

Замечание:  при  .

Рассмотрим также несколько случаев решения данного уравнения, при решении которых используется единичная окружность.

4.3. Уравнение tgx = a (вспомнить линию tgx на окружности!)

Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = a имеет корни при любом значении а.

Решим уравнение tg x = . Для решения данного уравнения вспомним как вычисляется арктангенс числа.

Примеры. arсtg 1= , так как tg  = 1 и   <   <

          arсtg = - , так как tg (-) =  и   <   < .

Для решения уравнения tg x = a необходимо воспользоваться следующей схемой.

- Решим уравнение tg x = .

Так как a = , то воспользуемся  следующей формулой 

x = arctg a + πn,n є Z

x = arctg  + πn,n є Z

x =  + πn,n є Z - решение уравнения.

- Решить уравнение tg x = 2.

x = arctg a + πn,n є Z

x = arctg 2 + πn,n є Z - решение уравнения.

Т.о.

4.4. Уравнение ctgx = a. Аналогично рассматривается

Рассмотрим пример.

5. Первичное применение приобретенных знаний

5.1. Работа у доски

№ 1. Решить уравнения:

а)              б)

5.2. Работа в группах. Далее проводим проверку и разбор решения по ответам на экране.

№ 2. Решить уравнения

5.3.Работа с учебником.  № 16.5, 18.3, 573, 591, 611,

6. Подведение итогов

¾    С каким математическим понятием вы познакомились на уроке?

¾    Как решать простейшие тригонометрические уравнения?

¾    Что вызвало затруднение и почему?

¾    Как выходили из затруднений?

¾    Что Вам понравилось на уроке и почему?

¾    Ребята, в начале урока Вы поставили цели урока. Достигли мы их? (Целей достигли, так как 1.Изучили понятие простейших тригонометрических уравнений

2.Отработали умения  решать уравнения)

7. Домашнее задание. Л 8. №  21.28, 22.10