Тема: Исследование в задачах на построение циркулем и линейкой

Тема: Исследование в задачах на построение циркулем и линейкой

Цель занятия: научить обучающихся проводить исследование при решении задач на построение циркулем и линейкой.

Задачи:

1. Изучить метод решения задач при помощи циркуля и линейки.

2. Организовать самостоятельное исследование обучающихся при решении некоторых задач на построение, связанных с взаимным расположением прямых и окружностей.

3. Изучить возможности компьютерной программы «GeoGebra «для геометрических построений.

Мотивация деятельности: Геометрические задачи на построение, возможно, самые древние математические задачи. Сейчас они могут показаться не очень интересными, в самом деле, где и зачем может понадобиться умение с помощью циркуля и линейки построить правильный семнадцатиугольник или треугольник по трем высотам. Но даже с помощью современных технических устройств, которые сделают все эти построения и быстрее, и точнее, чем любой человек, а заодно смогут выполнить и такие построения, которые просто невозможно выполнить при помощи циркуля и линейки, решение и особенно исследование в таких задачах развивают творчество и математическое мышление.

При решении задач на построение выделяют следующие этапы: анализ, построение, доказательство, исследование.

Исследование — ответ на вопрос: всегда ли задача имеет решение, если да, то, сколько и есть ли частные случаи, требующие особого рассмотрения.

Сегодня мы рассмотрим решение пяти задач на построение циркулем и линейкой, которые связаны с исследованием взаимного расположения окружностей и прямых. Задачи интересны тем, что этап исследования в этих задачах содержит несколько случаев.

Ход работы:

Задача 1: Построить окружность данного радиуса, касающуюся данной прямой в данной точке.

Анализ: Центр окружности должен располагаться на перпендикуляре к прямой а, проходящем через заданную точку.

Построение выполнено с помощью программы GeoGebra:

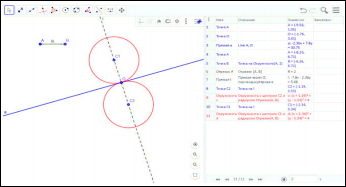
Исследование: Данная задача имеет два решения.

Задача 2: Построить окружность, проходящую через данную точку А и  касающуюся данной прямой в данной точке В.

Анализ: радиус, проведенный в точку касания перпендикулярен касательной. Центр равноудалён от А и В, значит лежит на серединном перпендикуляре к АВ.

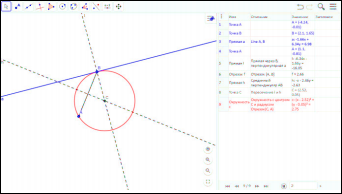
Исследование: В первом случае, когда точка А не принадлежит прямой а, одно решение.

Второй случай: Точка А принадлежит прямой а.

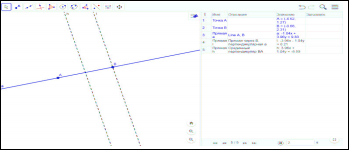
Решений нет, так как перпендикуляры к одной прямой не пересекаются.

Третий случай: Точки А и В совпадают.

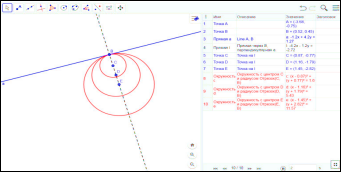
Решений множество.

Задача 3: Построить окружность, касающуюся двух данных прямых, причем одной из них в данной точке.

Анализ: Центр окружности должен располагаться на перпендикуляре к прямой а, проведенному из точки В. Так как центр искомой окружности равноудален от прямых а и b, значит он расположен на биссектрисе угла образованного прямыми a и b.

Исследование: В первом случае, когда прямые пересеклись одно решение задачи.

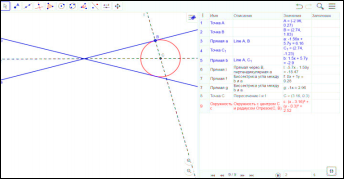
Второй случай: Прямые параллельны.

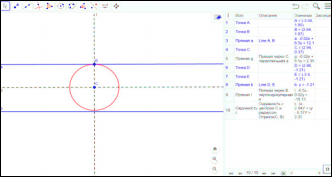
В данном случае одно решение.

Задача 4: Построить окружность, которая проходила бы через данную точку и касалась бы данной окружности в данной точке.

Анализ: Центр искомой окружности лежит на серединном перпендикуляре к АВ. Центр искомой окружности и центр данной окружности, и точка А располагается на одной прямой.

Исследование: В первом случаем, когда точка В располагается вне окружности, одно решение.

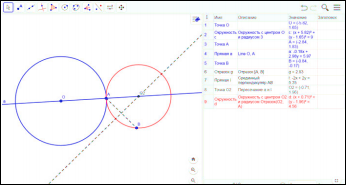
Второй случай: точки А и В лежат на одной окружности:

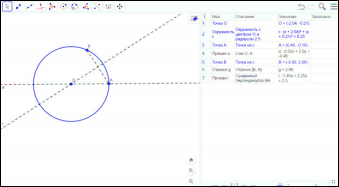
В данном случае решений нет, так как окружности должны иметь 2 общие точки, то есть касаться не смогут.

Третий случай: точка В внутри данной окружности.

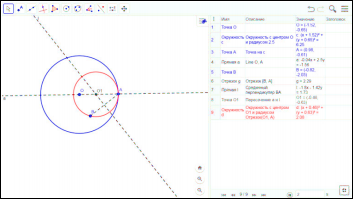
В данном случае одно решение.

Задача 5: Построить окружность данного радиуса, касающуюся двух данных окружностей.

Анализ: Радиус концентрических окружностей будет равен r+r¹ и r+r²

Центр искомой окружности будет расположен на пересечении или касании концентрических окружностей.

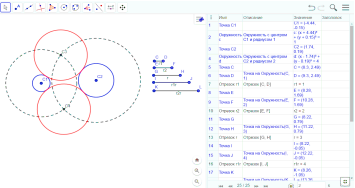
Исследование: В первом случае, когда концентрические окружности пересеклись в двух точках — два решения.

Второй случай: концентрические окружности имеют одну общую точку.

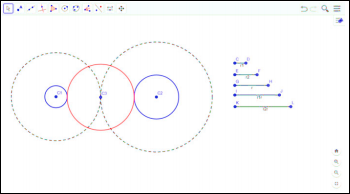
В этом случае одно решение.

Третий случай: когда концентрические окружности не имеют общих точек

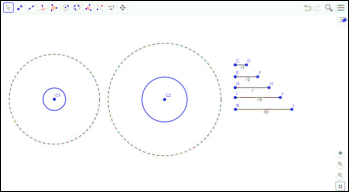
В данном случае нет решений.

Четвертый случай: концентрические окружности касаются внутренним образом.

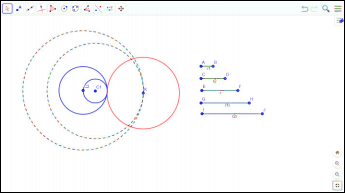
В данном случае одно решение.

Применение разработанных рекомендаций при решении задач на построение будет способствовать наиболее эффективному творческому поиску путей решения задач при изучении геометрии в курсе основной школы.

Скачано с www.znanio.ru