Дата проведения: 18.10.2011 Класс 8 «А»
Тема: «Трапеция. Средняя линия трапеции»
Урок изучение нового материала.
Цели урока:
Образовательные - ознакомить учащихся с новым видом четырёхугольника - трапецией, элементами трапеции;
Воспитательные - обеспечить интерес учащихся путём акцентирования элемента новизны: учащиеся знакомятся с новым видом четырёхугольника
Развивающие - развить умение анализировать, сравнивать, делать выводы при доказательстве теорем о средней линии трапеции.
План урока:
1. Организационный момент.(1 мин)
2. Введение определения трапеция(4 мин)
3. Закрепление понятия трапеция (2мин)
4. Знакомство с элементами трапеции.(3мин)
5. Виды трапеции(3мин)
6. Определение средней линии трапеции(3 мин)
7. Признак средней линии трапеции(3мин)
8. Свойства средней линии трапеции (3мин)
9. Доказательство свойств средней линии трапеции(5 мин)
10. Закрепление знаний о средней линии трапеции (5 мин)
11. Свойства равнобедренной трапеции(5 мин)
12. Закрепление знаний о равнобедренной трапеции(5 мин)
13. Задание на дом (1мин)
14. Рефлексия (2 мин)
Оборудование: учебник Шлыков «геометрия 8 класс»,схема «четырёхугольник», рисунки трапеций, элементов трапеции, средней линии трапеции.
Формы организации деятельности: индивидуальная, фронтальная.
Методы: эвристическая беседа, иллюстрации, сравнение, рассказ .
Ход урока:
1, Организационный момент
Учитель : «Здравствуйте, ребята! Все присутствуют на уроке?»
2, Введение определения трапеция
Учитель
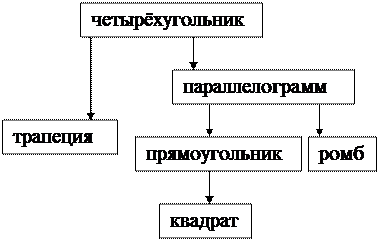
: «Давайте вспомним, с какими видами четырёхугольника мы с вами уже
познакомились на прошлых уроках?»
Учащиеся: «Параллелограмм, прямоугольник, ромб , квадрат.»
Учитель: «Верно. Сегодня мы познакомимся с ещё одним вводом четырёхугольника - трапеция.»
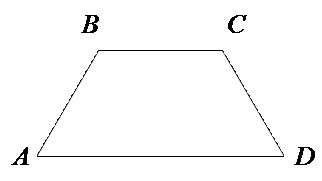
Учитель : «Записываем. Дата, Классная работа, тема «Трапеция. Средняя линия трапеции». Записываем определение трапецией называется четырёхугольник , у которой 2 стороны параллельны, а две другие не параллельны. Рисуем рисунок.»
 |
|||
|
|||
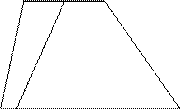
3.Закрепление понятия трапеция.
Учитель : «Найдите на рисунках трапеции.»
4. Знакомство с элементами трапеции.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитель:
«Из чего состоит трапеция? Записываем. Основаниями трапеции называются
параллельные стороны, а не параллельные называются боковыми сторонами. По
рисунку назовите основания и боковые стороны. »
5. Виды трапеции
Учитель: «Существует несколько видов трапеции: равнобедренная, или равнобокая, и прямоугольная трапеции. Какой треугольник называется равнобедренным?»
Учащиеся: «Треугольник называется равнобедренным если у него две стороны равны.»
Учитель: «А как вы думаете какая трапеция называется равнобокой?»
Учащиеся : «Тоже какие- то две стороны равны.»
Учитель: «Верно, а какие основания или боковые стороны? Могут ли основания быть равными?»
Учащиеся : «Нет, тогда бы этот четырёхугольник был параллелограммом. Значит, остаются боковые стороны.»
Учитель: «Совершенно верно. Записываем трапеция называется равнобедренной или равнобокой, если равны её боковые стороны. Рисуем рисунок»
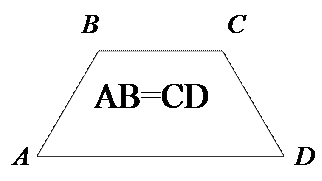
Учитель: «А какая трапеция будет называется прямоугольной?»
Учащиеся : «Трапеция называется прямоугольной, если один из её углов прямой.»
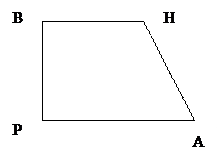Учитель
: «Верно. Записываем, трапеция называется прямоугольной, если один из её углов
прямой. Рисуем»
6. Определение средней линии трапеции.
Учитель: «Давайте вспомним, определение средней линии треугольника. »
Учащиеся: «Средней линией треугольника называется отрезок, соединяющий середины двух сторон треугольника.»
Учитель: «У трапеции также есть средняя линия. Как вы думаете что такое средняя линия трапеции?»
Учащиеся : «Наверно, отрезок, соединяющий боковые стороны трапеции.»
Учитель: «Верно. Записываем средней линией трапеции называется отрезок соединяющий середины боковых сторон трапеции. Рисуем.»
 |
|||
|
|||
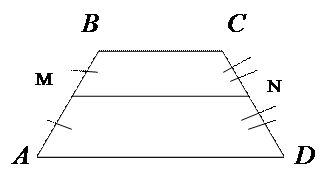
7. Признак средней линии трапеции
Учитель: «Сейчас мы рассмотрим признак средней линии трапеции. Давайте вспомним признак средней линии треугольника.»
Учащиеся: «Если отрезок параллелен стороне треугольника и его концы лежат на двух сторонах причём так, что один из концов является серединой стороны, то этот отрезок является средней линией треугольника.»
Учитель: «Как вы думаете какой будет признак средней линии трапеции. Если в треугольнике : Если отрезок параллелен стороне треугольника, то как будет в трапеции. Чему может быть параллельна средняя линия трапеции?»
Учащиеся: «Если отрезок параллелен одному из оснований трапеции»
Учитель: «Хорошо. Концы отрезка , где будут лежать в трапеции?»
Учащиеся: «Концы отрезка лежат на боковых сторонах»
Учитель: «Совершенно верно. Записываем признак средней линии трапеции: Если отрезок параллелен одному из оснований трапеции и концы отрезка лежат на боковых сторонах, а один из есть середина стороны, то этот отрезок является средней линией трапеции. Давайте ещё раз проговорим признак.»
Учащиеся: «Если отрезок параллелен одному из оснований трапеции и концы отрезка лежат на боковых сторонах, а один из есть середина стороны, то этот отрезок является средней линией трапеции»
8. Свойства средней линии трапеции
Учитель: «Давайте теперь выясним свойства средней линии трапеции. Давайте вспомним, какие свойства были у средней линии треугольника?»
Учащиеся: «Средняя линия треугольника параллельна третьей стороне и равна её половине»
Учитель: «А чему параллельна средняя линия трапеции?»
Учащиеся: «Средняя линия трапеции параллельна основаниям.»
Учитель: «Совершенно верно. Записываем свойство средней линии трапеции: Средняя линия трапеции параллельна основаниям , а её длина равна полусумме длин оснований. Давайте все вместе проговорим свойства.»
Учащиеся: «Средняя линия трапеции параллельна основаниям , а её длина равна полусумме длин оснований»
9.Доказательство свойств средней линии трапеции
Учитель: «Давайте докажем эти свойства. Еще раз проговорим свойства.»
Учащиеся: «Средняя линия трапеции параллельна основаниям , а её длина равна полусумме длин оснований.»
Учитель: «Что нам дано? Что необходимо сделать?»
Учащиеся: «Нам дана трапеция, средняя линия трапеции. Необходимо доказать, что средняя линия трапеции параллельна основаниям и её длина равно полусумме длин оснований»
Учитель: «Рисуем рисунок, отмечаем на нём известные данные.»
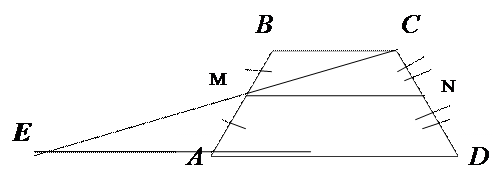
Учитель: «Давайте запишем дано.»
Дано: АВСD- трапеция, МN - средняя линия трапеции
Доказать: МN||АD и МN||ВС
МN=1/2*(АD+ВС)
Учитель: «Давайте дополним рисунок. Проведём прямую СМ до пересечения с АD и назовём точку Е. Что можно сказать про треугольника ЕАМ и ВСМ»
Учащиеся: «Они равны»
Учитель: «Почему? По Какому признаку?»
Учащиеся: «ВМ=МА- по условию, ∟ЕАМ=∟СВМ накрест лежащие , ∟ВМС=∟ЕМА вертикальные, значит треугольники равны по 2 признаку»
Учитель: «Что следует из равенства треугольников ЕАМ и ВСМ?»
Учащиеся: «ВС=ЕА и СМ=МЕ»
Учитель: «Какой можно рассмотреть треугольник?»
Учащиеся: «∆ЕСD»
Учитель: «Что можно сказать про отрезок МN»
Учащиеся: «МN средняя линия треугольника ЕСD по определению»
Учитель: «Что из этого следует? Какое свойства мы знаем средней линии треугольника?»
Учащиеся: «МN||ЕD, следовательно, МN||АD, а т.к. АВСD- трапеция, значит, ВС||АD, следовательно, МN||ВС»
Учитель: «Какое ещё есть свойство средней линии треугольника?»
Учащиеся: «МN=1/2*ЕD=1/2*(ЕА+АD)=1/2*(ВС+АD)»
Учитель: «Мы доказали. Теперь запишем доказательство»
Доказательство:
1, Дополнительное построение CM, E=CM ∩ AD
2,Рассмотрим ΔEMA и ΔCMB:
а) AM=MB (по условию MN-средняя линия)
б) ÐA = ÐB (накрест лежащие при BC||AD и секущей AB)
в) ÐAME = ÐBMC (вертикальные углы)
По 2 признаку равенства треугольника ΔEMA = ΔCMB
3,Из ΔEMA=ΔCMB:а) EA=BC б) EM=MC. ΔECD : ЕМ=МС и CN=ND, значит, MN – средняя линия ΔECD, тогда по свойству средней линии треугольника
1) MN||ED, то есть MN || AD ,BC || AD, следовательно, MN || BC
2) MN = ½ ED = ½ (EA+AD) = ½ (BC+AD)
Ч.т.д.
10.Закрепление знаний о средней линии трапеции
|
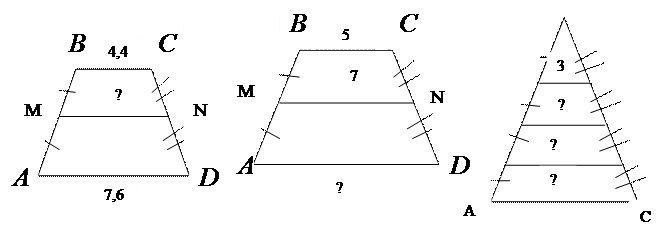
11.Свойства равнобедренной трапеции
Учитель: «Записываем свойства равнобедренной трапеции. 1свойство равнобедренной трапеции: углы при каждом основании равнобедренной трапеции равны. Давайте нарисуем рисунок. Какие углы будут равны?»
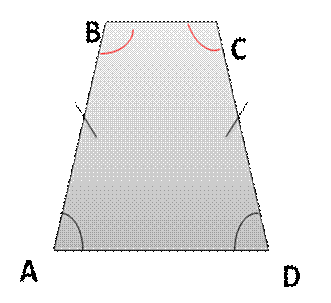
Учащиеся: «∟А=∟D и ∟В=∟С»
Учитель: «Совершенно верно. Молодцы. Давайте проговорим 1 свойство равнобедренно трапеции.»
Учащиеся: «Углы при каждом основании равнобедренной трапеции равны.»
Учитель: «Записываем 2 свойство равнобедренной трапеции: Диагонали равнобедренной трапеции равны. Делаем рисунок. Проговорим ещё раз это свойство.»
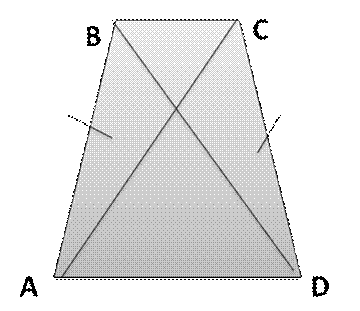
Учащиеся: «Диагонали равнобедренной трапеции равны.»
12.Закрепление знаний о равнобедренной трапеции
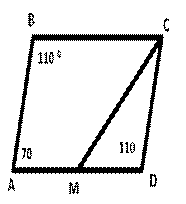
Учитель: «По рисунку найти неизвестные.»
 |
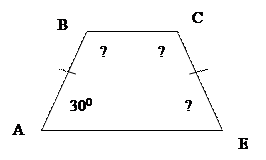13.Задание на дом
Д/з §6 № 118,120
Учитель: «В домашнем задании вам необходимо будет доказать, что четырёхугольник является трапецией. Как вы это будете доказывать?»
Учащиеся: «У трапеции 2 стороны параллельны , а две другие не параллельны.»
Учитель: «Как будете доказывать, что две стороны не параллельны? Что значит, что прямые не параллельны?»
Учащиеся: «Это ,значит, что они пересекаются»
14.Рефлексия
Учитель: «С каким четырёхугольником мы сегодня познакомились?»
Учащиеся: «Трапеция»
Учитель: «Определение трапеции»
Учащиеся: «Трапецией называется четырёхугольник, у которого 2 стороны параллельны, 2 другие не параллельны.»
Учитель: «Какие виды трапеции вы знаете?»
Учащиеся: «Прямоугольная и равнобедренная»
Учитель: «Давайте вспомним определение средней линии трапеции.»
Учащиеся: «Средней линией треугольника называется отрезок, соединяющий середины двух сторон треугольника.»
Учитель: «А какими свойствами обладает средняя линия трапеции?»
Учащиеся: «Средняя линия трапеции параллельна основаниям , а её длина равна полусумме длин оснований»
Учитель: «С какими свойствами равнобедренной трапеции вы познакомились?»
Учащиеся: «Диагонали равнобедренной трапеции равны и углы при каждом основании равнобедренной трапеции равны.»
Учитель: «Молодцы.»
Дата проведения: 18.10.2011
Учитель : «Записываем. Дата, Классная работа, тема «Трапеция
Учитель: «Существует несколько видов трапеции: равнобедренная, или равнобокая, и прямоугольная трапеции
Учитель: «Верно. Записываем средней линией трапеции называется отрезок соединяющий середины боковых сторон трапеции
Учащиеся: «Средняя линия трапеции параллельна основаниям , а её длина равна полусумме длин оснований
AM = MB (по условию MN -средняя линия) б) Ð
Учитель: «Совершенно верно. Молодцы
Рефлексия Учитель: «С каким четырёхугольником мы сегодня познакомились?»
© ООО «Знанио»
С вами с 2009 года.
