Тема: "Цилиндр. Основные понятия". Практическое задание.

Цилиндр. Основные понятия

Цилиндр – это один из видов тел вращения. Вокруг нас существует множество предметов, имеющих форму цилиндра. Кружки и стаканы имеют форму цилиндра, карандаши, шляпы, коробки, пуфики, некоторые архитектурные сооружения и многое другое.

Итак, если взять некоторый прямоугольник ABCD и вращать его вокруг одной из сторон, например, вокруг стороны AB, то в результате получим тело, которое и называется цилиндром.

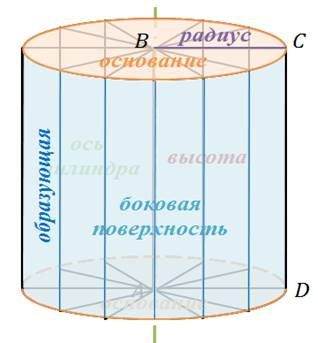
Прямая AB называется осью цилиндра. Отрезок AB – его высотой.

При вращении сторон AD и BC образуются два равных круга – они называются основаниями цилиндра, а их радиус называется радиусом цилиндра.

При вращении стороны CD образуется поверхность, состоящая из отрезков, параллельных оси цилиндра. Ее называют цилиндрической поверхностью или боковой поверхностью цилиндра. Отрезки, из которых она составлена называют образующими цилиндра.

Определение. Цилиндр – это тело, ограниченное двумя равными кругами и цилиндрической поверхностью.

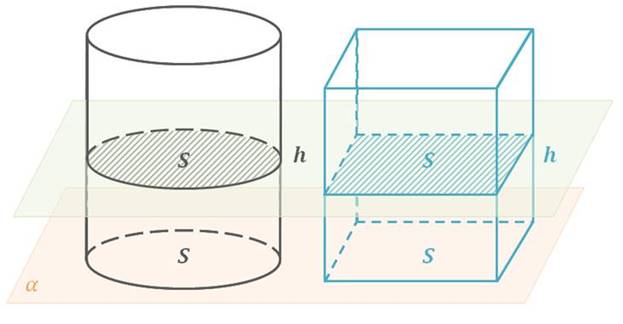
Рассмотрим цилиндр и призму с площадями оснований, равными S, и высотами, равными h, «стоящие» на одной плоскости. Любая секущая плоскость, параллельная этой плоскости, дает в качестве сечения цилиндра круг площади S, а в качестве сечения призмы – многоугольник площади S. Значит, объем цилиндра равен объему призмы . Но ведь объем призмы равен произведению площади основания на высоту . А значит, и объем цилиндра равен произведению площади основания на высоту:

.

На рисунке изображен цилиндр с радиусом r и высотой h. Давайте представим, что боковую поверхность цилиндра разрезали по образующей AB и развернули таким образом, что получился прямоугольник ABB’A’.

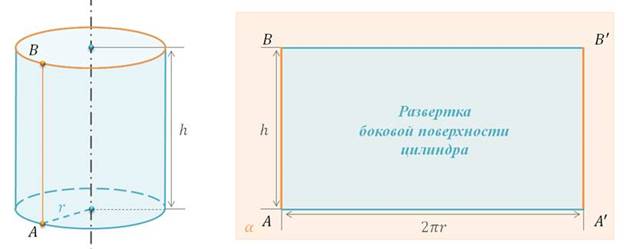
Стороны AB и A’B’ которого являются двумя краями разреза боковой поверхности цилиндра. Этот прямоугольник называется разверткой боковой поверхности цилиндра.

Обратите внимание, сторона AA’ прямоугольника равна длине окружности основания, а сторона AB равна высоте цилиндра, т.е. AA’ =2πr, AB=h.

Площадь боковой поверхности цилиндра равна площади ее развертки. А так как развертка боковой поверхности цилиндра есть прямоугольник, то площадь
боковой поверхности .

Основания цилиндра – два круга, каждый с площадью . А тогда полную поверхность цилиндра можно вычислить, как сумму площади боковой поверхности цилиндра и площадей двух оснований. Отсюда, видим, что площадь полной поверхности цилиндра . 

Задачи по теме: «Цилиндр»

Задача 1. Диаметр основания цилиндра равен 2 см. Найдите площадь полной поверхности цилиндра, если высота цилиндра равна длине окружности основания.

Решение: напомню, что площадь полной поверхности цилиндра равна сумме площади боковой поверхности цилиндра и площадей двух оснований.

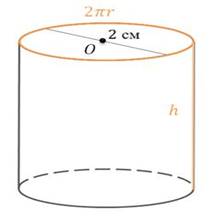
 см

 (см)

 (см²)

Ответ: .

Задача 2. Высота цилиндра 6  см, а радиус основания – 5  см. Вычислите объем цилиндра.

Решение. Объем цилиндра равен произведению площади основания на высоту.

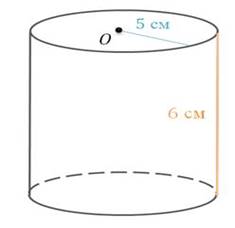
   (см³)

Ответ: .

Задание по теме: «Цилиндр».

1. Нарисуйте в тетради цилиндр и нанесите основные элементы цилиндра.

2.Изобразите:

 а) осевое сечение цилиндра; 

б) сечение цилиндра плоскостью, проходящей перпендикулярно оси цилиндра;

 в) сечение цилиндра плоскостью, проходящей параллельно оси цилиндра.

Какая фигура получается в каждом случае?

3. Запишите формулы для вычисления площади поверхности цилиндра.

Что можно найти по этим формулам? Что должно быть известно в этих случаях?

4. Приведите примеры использования цилиндров.

5. Произвести расчет расхода материала на изготовление консервной банки по представленной в презентации развертке. На обрезку, сгибы, фигурную штамповку и прочее уходит 10% материала.

Задача 1. Диаметр основания цилиндра равен 6 см. Найдите площадь полной поверхности цилиндра, если высота цилиндра равна длине окружности основания.

Задача 2. Высота цилиндра 8 см, а радиус основания – 4  см. Вычислите объем цилиндра.