Тема урока: Определение дифференциала функции, его геометрический смысл.

   Урок №

Тема урока: Сложная функция и ее производная.

Цели урока:

1.      Обучающая: Рассмотреть понятие сложной функции, формулу для её нахождения, показать практическое применение.

2.      Развивающая: способствовать развитию логического мышления, памяти.

        3. Воспитательная: Аккуратное ведение конспектов, самодисциплина.

       Тип  урока: Урок изучения нового материала

       Вид урока: лекция

       Методы:  словесные        

       Оборудование: раздаточный материал по теме урока.

Ход урока.

 I. Оргмомент

II. Актуализация опорных знаний

       Устный опрос

 II. Целевая установка.

1.     Тема урока                          

2.     Цель урока

III. Формирование новых понятий и способов действий.

Сложная функция – это функция, аргументом которой также является функция.

Формула нахождения производной сложной функции.

IV.  Формирование навыков умственного труда

         Примеры:

1)    Найти производную сложной функции:

Решение:

2)    Найти производную сложной функции

Решение:

3)    Найти производную функции: 

Решение:

4)    Найти производную функции: 

Решение:

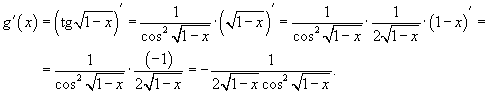
5) Найти производную функции: 

Решение:

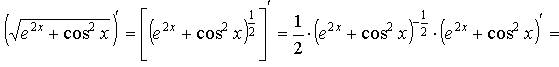
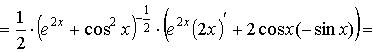
6)    Найти производную функции: 

V. Итог  урока.

     Подведение итогов, выводы.

VI. Домашнее задание:   

     Конспект.