Тема урока: Пр. занятие № 12. Решение линейных обыкновенных дифференциальных уравнений первого порядка

   Урок №

Тема урока: Пр. занятие № 12.

Решение линейных обыкновенных дифференциальных уравнений первого  порядка

Цели урока:

1. Обучающая: Применить теоретические знания при решении линейных обыкновенных дифференциальных уравнений первого  порядка.

2. Развивающая: Способствовать развитию логического мышления, памяти.

        3. Воспитательная: Аккуратное ведение конспектов, самодисциплина.

       Тип  урока: Урок совершенствования знаний и умений.

       Вид урока: Практикум

       Методы:  словесные, практические       

       Оборудование: Методические материалы для практического занятия № 12.

Ход урока.

 I. Оргмомент

II. Актуализация опорных знаний

      Устный опрос

 II. Целевая установка.

1.      Тема урока           2. Цель урока

III. Практическая часть урока

Пример 1. Найти общее решение дифференциального уравнения

Решение

Проведём замену: в исходное уравнение. Получим:

Составим систему. Для этого приравняем к нулю то, что находится в скобках v¢ + 2хv = 0, автоматически получая второе уравнение системы: 

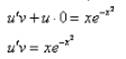
В результате:

Из первого уравнения найдём функцию v:

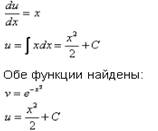
Пример 2: Найти частное решение дифференциального уравнения  , удовлетворяющее начальному условию у(1) = е

Решение

Проведём замену:  и подставим в исходное уравнение.

Подставим во второе уравнение и найдём функцию u:

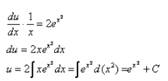
- общее решение

Из начального условия у(1) = е  найдём частное решение:

   - частное решение.

V.                 Самостоятельная работа

Ответы

VI. Домашнее задание:   

Решить дифференциальные уравнения :

1)           2)

2)