Поделиться
Тригонометрия_для_старшеклассников.PDF
В. А. Дорофеев
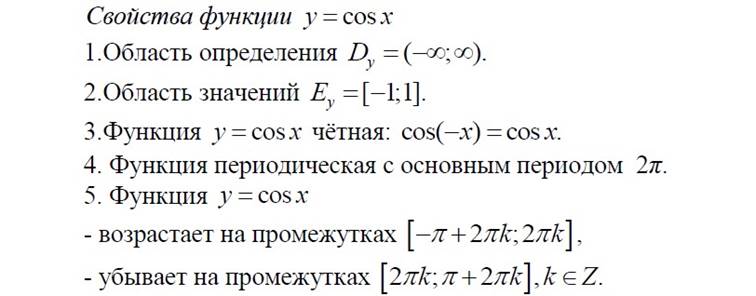
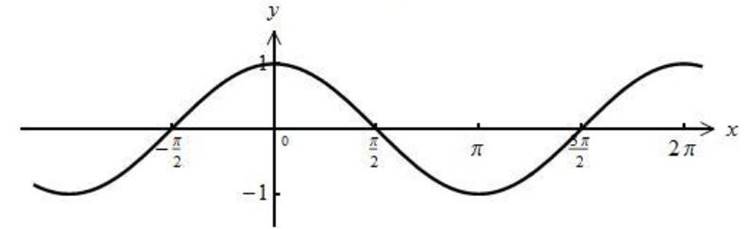y=cosx Рис.
4
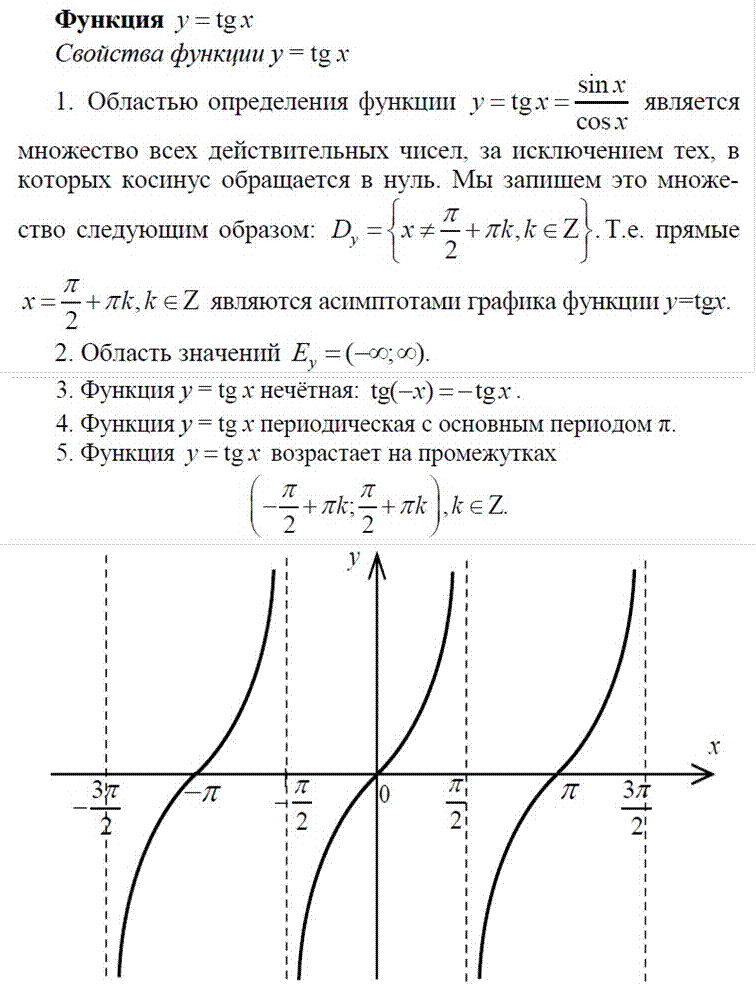y=tgx Рис. 5
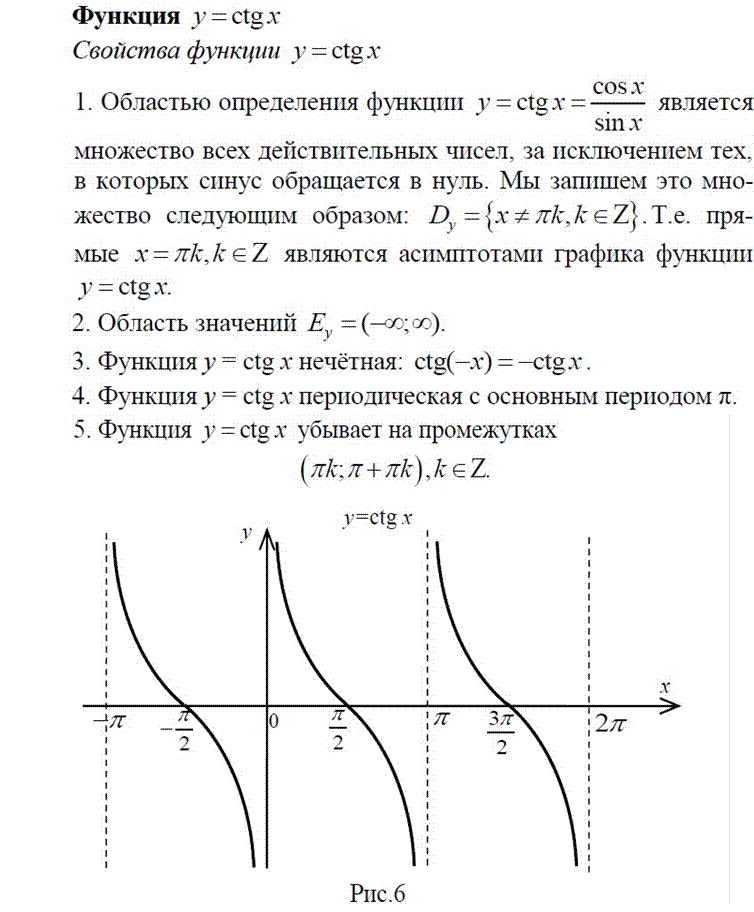
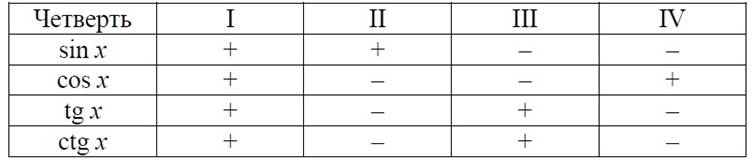
На тригонометрической окружности знаки тригонометрических функций располагаются следующим образом:
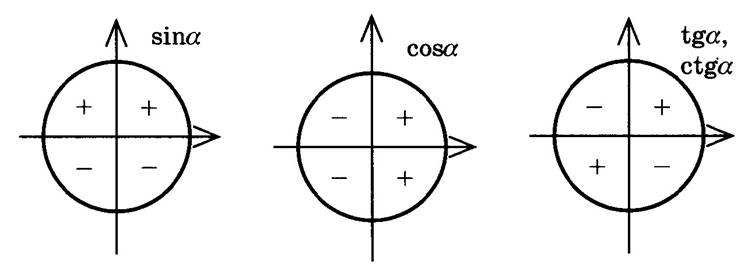
Запишем в таблице основные свойства тригонометрических функций:
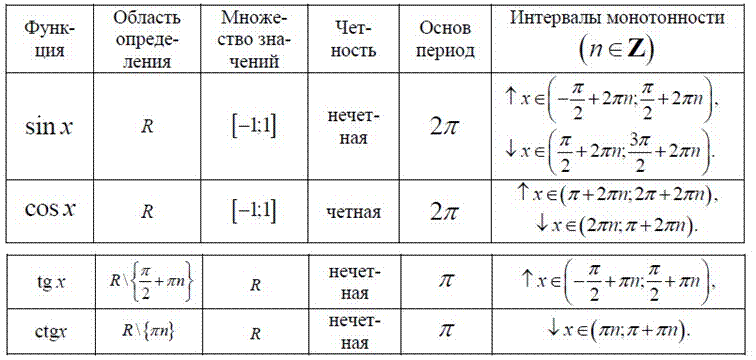
Данные правила можно сформулировать проще:
1. Если тригонометрическая функция не содержит дроби:
π±α, 2π±α,… kπ±α, то название функции сохраняется; если же тригонометрическая функция содержит в себе дроби вида:
, то название функции
меняется на ко-функцию (синус на косинус, тангенс на котангенс и наоборот).
2. Знак полученной после преобразования функции определяется по знаку первоначальной функции.
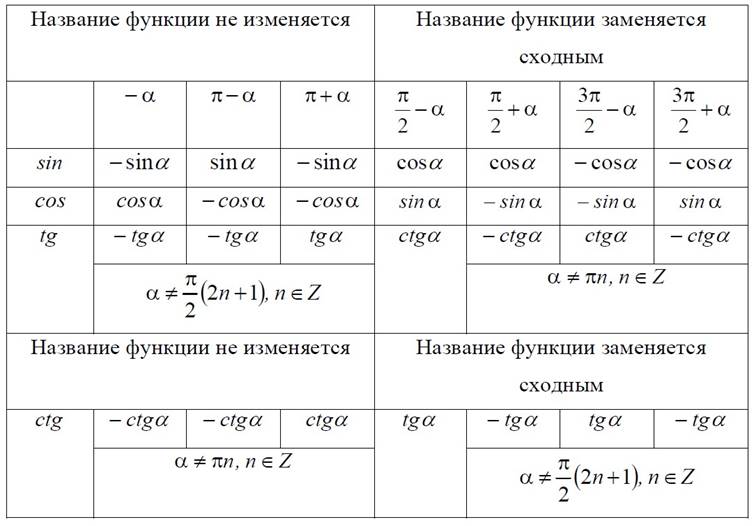
При применении формул приведения в решении упражнений и задач удобно использовать следующую таблицу:
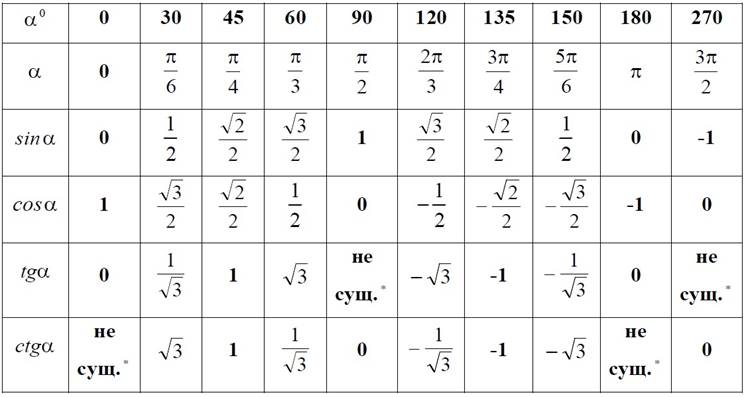
Расширим таблицу наиболее встречающихся углов в градусной и радианной мере и значений тригонометрических функций в этих углах:
Ответ: -sinα.
§7. Примеры решения типовых задач
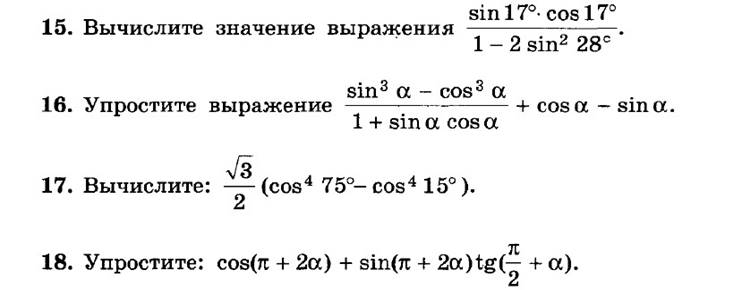
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
