Десятое ноября

Решение упражнений (повторение)

Сегодня на уроке мы закрепим материал предыдущих уроков, выполним различные упражнения, где нам будут встречаться математические действия I,II и III ступени. Давайте повторим их компоненты и очередность выполнения:

Решаем устно:

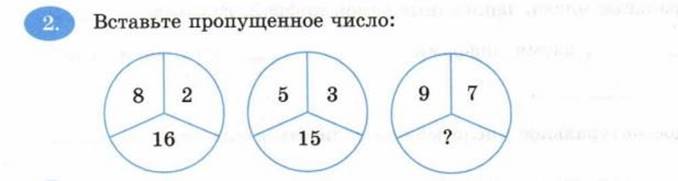
Если быть внимательным, можно заметить, что  и в первом, и во втором кружочках, в нижнем секторах записано произведение верхних секторов: 8·2=16, 5·3=15. Тогда несложно догадаться, какое же число кроется под знаком вопроса: 9·7=__.

Давайте устно заполним таблицу. Для этого вам, как всегда, понадобятся знания таблицы умножения.  Если вы забыли, что такое степень числа, переходите по ссылке на видео урок https://youtu.be/0y43sX6n7os  

Если число равно 9, то его квадрат = ___

Какое число нужно возвести в квадрат (умножить на само себя), чтобы получилось 16? __

Возведем 7 в квадрат (7²=7·7=__). 

Какое число при умножении на само себя даёт результат 64? __

2=8·8=__) Возведем 8 во вторую степень (8

Какое число при умножении на само себя даёт результат 25?

Возведем 10 во вторую степень (10²=10·10=__)

Какое число при умножении на само себя даёт результат 10000?

Если мы единицу возведем в квадрат? А если в куб? А если единицу возведем в 53 степень (т.е. умножим единицу саму на себя 53 раза)? Возведем в квадрат ноль. Получим ___

Итак, решим несколько разных упражнений 

№1

а) 7·52+3²= 

Возведение в степень является арифметический действием третьей ступени, умножение – второй, а сложение – третьей. Значит, первым действием будет возведение в степень (чем выше ступень, тем первее делается действие):

7·52+3²= 7·(5·5)+(3·3)=7·25+9= Второе действие – умножение:

7·25+9=175+9= Третье действие – сложение: 175+9=184.

б) 200-14²:7=

Снова определяем порядок действий: возведение в степень – первое, деление – второе, вычитание – третье.

200-14²:7=200-(14·14):7=200-196:7=200-28=172.

в) 6³:9-3=(6·6·6):9-3=216:9-3=24-3=21.

д) 700-(26²+24)=700-((26·26)+24)=700-(676+24)=700-700=0.

(Делаем запись в тетрадочку)

№2

Решите уравнения: а) (39-22)²-х=270

Итак, посмотрите на такое уравнение, в роли уменьшаемого у нас выражение (39-22)², вычитаемое – неизвестное х, а разность – 270.

Давайте упростим наше уменьшаемое, т.е. вычислим, сколько же будет (39-22)²:

17²-х=270

17·17-х=270

289-х=270 Уравнение приняло привычный для вас вид. 

х=289-270 х=19

Делаем проверку:

289-19=270

     270=270

б) 3⁵·у=6804:4

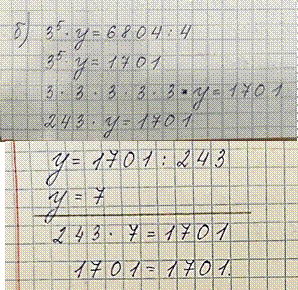В этом уравнении неизвестен множитель. Чтобы его найти, необходимо произведение (6804:4) разделить на известный множитель (3⁵):

3·3·3·3·3·у=1701 243·у=1701 у=1701:243 у=7 Проверяем:

243·7=1701

 1701=1701

в) р:9=2437-7⁴

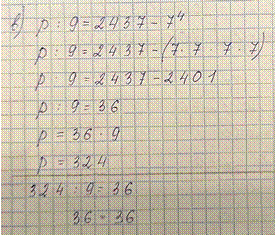В этом уравнении необходимо найти делимое. Чтобы найти делимое нужно частное (2437-7⁴) умножить на делитель (9).

р:9=2437-(7·7·7·7) р:9=2437-2401 р:9=36 р=36·9 р=324 Проверяем: 324:9=36

     36=36

№3

Вычислите значения произведений, используя распределительный закон:

а) 5·81=

б) 7·408=

в) 4·397=

г) 3·298=

Вспомним распределительный закон умножения. Если забыли, переходим по ссылке и смотрим видео урок:  https://youtu.be/On-ijzgJ3qA  

Распределительный закон умножения относительно сложения: чтобы сумму умножить на число, можно умножить на это число каждое из слагаемых, а затем сложить полученные произведения.

С помощью букв его записывают так: ( a + b ) • c = a • c + b • c . Пример: ( 2 + 4 ) • 3 = 2 • 3 + 4 • 3 = 6 + 12 = 18.

Распределительный закон умножения относительно вычитания: чтобы разность умножить на число, можно умножить на это число уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе произведение.

С помощью букв его записывают так: ( a - b ) • c = a • c - b • c . Пример: ( 6 - 4 ) • 3 = 6• 3 - 4 • 3 = 18 - 12 = 6.

Освежили в памяти, а теперь применим на практике, но в обратном порядке. Мы представим один множитель в виде суммы слагаемых так, чтобы нам было проще считать. В этом нет ничего сложного, мы это делали всегда при устном счете:

а) 5·81=5·(80+1)=5·80+5·1=400+5=405;

б) 7·408=7·(400+8)=7·400+7·8=2800+56=2856;

в) 4·397=4·(300+90+7)=4·300+4·90+4·7=1200+360+28=1588;

Но его можно вычислить еще проще, представив число 397 в виде разности чисел 400 и 3. Обратите внимание, что поскольку мы заменили множитель на разность чисел (использовали вычитание), то далее у нас появится знак минус:

4·397=4·(400-3)=4·400-4·3=1600-12=1588 г) 3·298= 3·(300-2)=3·300-3·2=900-6=894.