Урок геометрии "Прикладные задачи, связанные с объемом прямоугольного параллелепипеда""

Урок геометрии по теме "Прикладные задачи, связанные с объемом прямоугольного параллелепипеда". 11-й класс

Тучкова Елена Ивановна, учитель математики    Геометрия        

Цели урока:

• Образовательные:   ввести понятие объёма, рассмотреть свойства объёмов геометрических тел, рассмотреть формулу объёма прямоугольного параллелепипеда, рассмотреть решение основных типов задач (из банка заданий ЕГЭ) по теме,  учить решать задачи практического содержания
• Развивающие:   развивать логическое  мышление, пространственное воображение,  расширять представления об окружающем нас мире, развивать умение осуществлять самоконтроль
• Воспитательные:   воспитывать ответственное отношение к учебному труду, уважительное отношение к сверстникам, развивать умение оказывать взаимопомощь, воспитывать интерес к предмету.

Оборудование: набор карточек с формулами для вычисления площадей, презентации к уроку, мультимедийная установка.

Методы и приемы обучения:

1.      Методы формирования новых умений: упражнение: репродуктивное, поисковое

2.      Методы контроля и диагностики: опрос, наблюдение за текущей работой обучающихся.

Формы работы: фронтальная, групповая, индивидуальная

Практический опыт: применение полученных знаний на практике, решение прикладных задач.

ХОД УРОКА

1. Организационный этап

Учитель проверяет готовность учащихся к уроку и подготовленность классного помещения.

2. Проверка выполнения домашнего задания

Учитель: К сегодняшнему уроку вам предлагалось вспомнить формулы для вычисления площадей плоских фигур.

Учитель: Выполните взаимопроверку задания по карточкам.

Сегодня вам предстоит напряженная интеллектуальная и творческая деятельность. Чтобы она была эффективной нам понадобятся ваши знания и желание узнать что-то новое.

Давайте выполним следующие задания (кубик и куб)

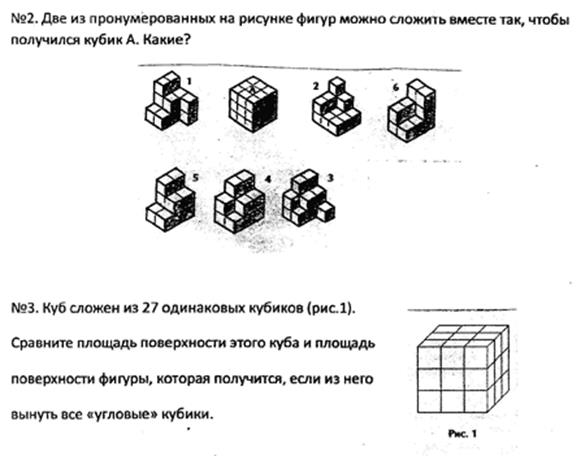
Рисунок 1

В ходе фронтальной беседы с классом обсуждаем получившиеся результаты:

№2. Фигуры  2 и  4;
№3. «останется без изменений»

3. Подготовка учащихся к работе на основном этапе

Учитель: При решении задач на уроках геометрии (в том числе и при решении задач ЕГЭ) нам очень часто приходится вычислять площади геометрических фигур.
Давайте вспомним соответствующие формулы (класс проверяет работу вызванного к доске ученика).
А теперь предлагаю вашему вниманию  задачи  из банка заданий ЕГЭ.

Задание 1. (Устно). Найдите площади фигур, изображённых на рисунке (клетка 1см х 1см).

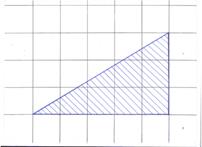
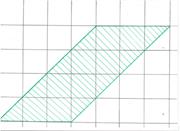
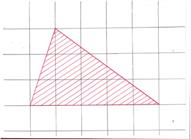
Учащиеся работают в тетрадях, а один из учеников решает задачу у доски.

4. Этап усвоения новых знаний и способов действий

Учитель: Что отличает геометрические тела, с которыми мы работаем на уроках стереометрии, от рассмотренных геометрических фигур?
Правильно, геометрические тела объёмные.
Итак, мы с вами приступаем к изучению ещё одного очень важного понятия – объём.

Тема урока: «Понятие объёма. Объём прямоугольного параллелепипеда»

Сегодня мы:

• совершим небольшой экскурс в историю
• узнаем, какими свойствами обладают объёмы
• вспомним, как вычисляется объём прямоугольного параллелепипеда
• посмотрим, как эти сведения используются на практике.

Учитель: В ближайшем будущем каждому из вас предстоит выбрать профессию. Какую роль играет в этом математика?

 Математика-это не только стройная система законов, теорем и задач, но и уникальное средство познания красоты. Многие математические теории нередко кажутся искусственными, оторванными от реальной жизни, просто непонятными. Если же подойти к этим проблемам с позиции исторического развития, то станет виден их глубокий жизненный смысл, их необходимость.

Математика и архитектура развивались одновременно. Нельзя было провести строгую границу между этими двумя видами искусств. В древности математика, как и архитектура, относилась к искусствам. Образование человека считалось неполным, если он, наряду с философией, поэзией, музыкой, не овладевал современной ему математикой, не умел ставить и решать задачи, доказывать теоремы. Развитие математики требовало знаний архитектуры и наоборот. Потребности зарождающегося строительства и, возникшей вслед за ним архитектуры явились одним из стимулов, благодаря которым возникла и сделала первые шаги математика.

Архитектура — древнейшая сфера человеческой деятельности и ее результат. Главный смысл понятия архитектура состоит в том, что это совокупность зданий и сооружений различного назначения, это пространство, созданное человеком и необходимое для его жизни и деятельности.

 Хороший архитектор должен знать аналитическую геометрию и математический анализ, основы высшей алгебры и теории матриц, владеть методами математического моделирования и оптимизации. Архитекторы имеют дело с математикой при сооружении различных объектов.

В современной архитектуре, да и не только в современной, используются различные формы, представляющие из себя известные нам геометрические тела.   Назовите эти тела.

Изучение теории объёмов мы начнём с достаточно часто встречающегося геометрического тела – прямоугольного параллелепипеда.

А теперь блиц-опрос.

• Сколько граней у прямоугольного параллелепипеда?
• Какими фигурами являются грани прямоугольного параллелепипеда?
• Сколько измерений у прямоугольного параллелепипеда?
• Как мы их обычно называем?
• Верно ли, что куб является прямоугольным параллелепипедом?
• Все грани куба – это …
• Назовите предметы окружающей обстановки, имеющие форму прямоугольного параллелепипеда.

Теперь давайте вспомним формулу, по которой вычисляется объём прямоугольного параллелепипеда. Эта формула хорошо вам известна из курса математики 5 класса.
Итак, как вычислить объём прямоугольного параллелепипеда?

Учитель на доске, а учащиеся в тетрадях записывают формулу V = abc

Свойство объемов многогранников - Некоторые свойства объёмов многогранников:

·         Равные тела имеют равные объёмы. 

·         Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел. 

·         Объём куба, ребро которого равно единице длины, равен единице. 

5. Этап закрепления новых знаний и способов действий

Учитель: Пришла пора потренироваться в решении задач на нахождение объёмов прямоугольных параллелепипедов. Прежде, чем мы приступим к решению задачи, мальчики помогут нам узнать три измерения нашего кабинета  с помощь рулетки. Девочки оформят решение на доске.

Задача 1. Кабинет, в котором проходит наш урок, имеет форму прямоугольного параллелепипеда с измерениями 6,5 м, 8 м и 3,6 м. По принятым санитарным нормам на одного учащегося в учебном кабинете должно приходиться не менее 6 м³ воздуха. Какое наибольшее количество учащихся можно разместить в этом кабинете, не нарушая санитарных правил?

(Дети решают эту задачу самостоятельно в своих тетрадях, после чего обсуждаем получившиеся результаты).

Решение. Вычислим объём классной комнаты: 6,5 ^. 8 ^. 3,6 = 187,2 м³ . Узнаем, сколько учащихся можно разместить в этом помещении, при условии, что на одного учащегося приходится 6 м³ воздуха: 187,2 : 6 = 31,2. Следовательно, в кабинете может заниматься 31 ученик.

Учитель: Ребята, задачи такого вида называются прикладными. Прикладная задача — это задача, поставленная вне математики и решаемая математическими средствами. 

Решение прикладной задачи состоит из нескольких этапов: составление математической модели, применение алгоритмов (схем) решения, вычислительный процесс и ответ на поставленный вопрос.

Сегодня мы с вами будем решать задачи, связанные с объемом прямоугольного параллелепипеда.

. Прикладная задача — это задача, поставленная вне математики и решаемая математическими средствами. 

Летом в нашем крае очень жарко и каждый человек мечтает повести летние месяцы комфортно. Кто-то уезжает туда, где есть море, а кто-то делает бассейн у себя дома. Решим следующую задачу.

n  Задача № 2.  Вычислить объем бетона, который требуется, чтобы залить дно в бассейне, если его толщина должная быть 10 см, размеры бассейна 5 м ×3 м. Сколько нужно кг цемента, если на 1 уходит 4 мешка по 4 кг?

Задача № 3.

Представьте, что вы владелец магазина. ЗАО Холод, производитель Пятигорского мороженого, предложил вам определенное количество мороженого Пломбир с большой скидкой. Как вы сможете определить полезную емкость морозильной камеры, если она

имеет форму прямоугольного параллелепипеда размерами 2×1,5×3?

Сколько металлических шариков на картинке?

В одном кубике 216 шариков.

На рисунке 5 кубиков.

Всего получим 1080 шариков.

Ответ: На рисунке 1080 шариков.

При подготовке к ЕГЭ вам наверняка встречались задания на нахождение объёмов многогранников такого вида. В процессе обсуждения способов решения задачи вспоминаем изученное на уроке свойство объёмов, которое позволяет нам разбивать многогранник на части, объёмы которых мы в состоянии вычислить.

6.  Применение знаний и способов действий

На этом этапе урока учащиеся работают в группах по 4 человека. Каждой группе предлагается карточка с заданиями по изученному на уроке материалу.

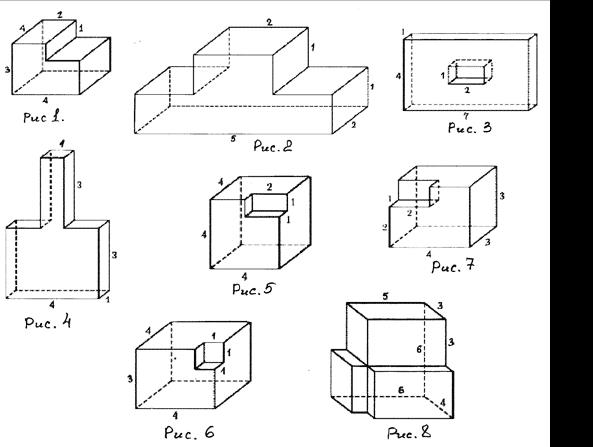
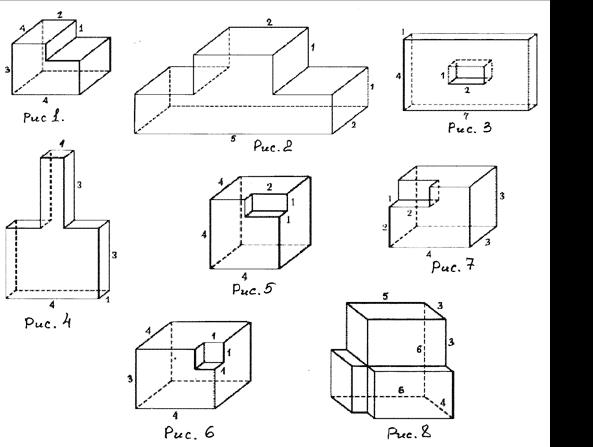
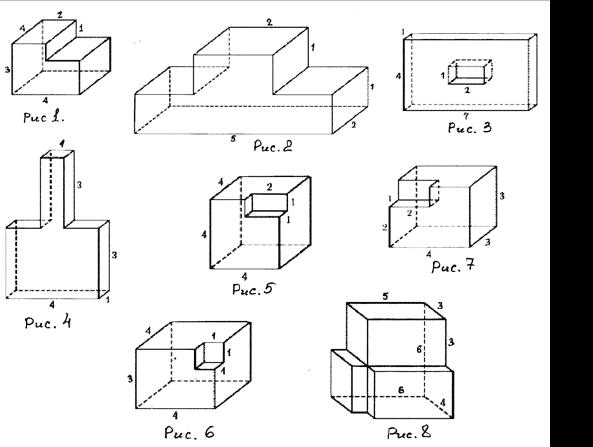
Рисунок 5

На работу в группе отводится 7 минут.
По окончании работы полученные результаты обсуждаются

7. Контроль и самоконтроль знаний и способов действий

Учащиеся в тетрадях выполняют задания математического диктанта:

• Заполни пропуски: «Равные тела имеют … объёмы».
• Заполни пропуски: «Если тело составлено из нескольких тел, то его объём равен … объёмов этих тел».
• Заполни пропуски: «Объём прямоугольного параллелепипеда равен … трёх его измерений».
• Заполни пропуски: «Объём куба равен … его ребра».
• Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
• Измерения прямоугольного параллелепипеда равны 10 см, 10 см и 5 см. Найдите ребро куба, объём которого в 2 раза больше объёма данного параллелепипеда.
• Во сколько раз нужно увеличить каждое из трёх измерений прямоугольного бруса, чтобы объём его увеличился в 8 раз?

8. Информация о домашнем задании

а) подобрать, используя различные ресурсы, 2-3 задачи рассмотренных на уроке типов из банка заданий ЕГЭ
б) выполните задание на карточке: «Когда человеку уютно, приятно, спокойно, он говорит, что ему комфортно. Оказывается, комфортность определяется формой помещения, его линейными размерами. Коэффициент комфортности можно найти по формуле:  , где  – коэффициент комфортности, V – объём жилища, S – площадь поверхности жилища, включая пол. Чем меньше коэффициент, тем комфортнее жилище. Используя данную формулу, определите наиболее комфортную комнату в вашей квартире».

9. Рефлексия

n  Что для вас на уроке было неожиданным?

n  В задачах какого вида вам хотелось бы разобраться более подробно и отработать навыки решения?

n  Как вы считаете, прикладные задачи могут повысить мотивацию к изучению геометрии?

Ребята, а кому из вас сегодняшний урок поможет лучше подготовиться к сдаче ЕГЭ?

10. Подведение итогов занятия

Учитель даёт качественную оценку работы класса и отдельных учащихся.
Спасибо за урок!

Скачано с www.znanio.ru