Урок "Графическое решение уравнений"

Урок по математике «ГРАФИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ»

Учитель математики Рогова Ю.В.

 Цель урока: - научить решать графически уравнения;

                      - повторить графики и свойства основных элементарных функций.

Тип учебного занятия: урок изучения и первичного закрепления новых знаний.

Ход урока.

I.                    Устный счет (ОГЭ задание №1. Действия со степенями. Онлайн. Решу. ОГЭ)

II.                 Актуализация.

1.Выбрать способ решения уравнений, представленных на слайде.

Правильно, но до этого урока мы решали уравнения аналитически, т.е. с помощью вычислений. Сегодня нам предстоит научиться решать уравнения другим способом, а именно с помощью построения графиков. Открываем рабочие тетради и записываем тему урока «Графическое решение уравнений».

В ходе нашего урока мы повторим, какие функции нам известны, их свойства и графики;  научимся определять число корней уравнения с помощью графиков; найдём схему решения уравнений с помощью графиков; решим вместе уравнения, а в конце урока вы попробуете решить уравнение самостоятельно. Давайте сформулируем цель урока.

Ученики: Научиться решать уравнения с помощью графиков.

Учитель: Какие функции мы знаем и какие линии являются их графиками?

Ученики  1 ряд изображает график, 2 ряд название графика, 3 ряд аналитическую запись функции:

·         Линейная функция, графиком является прямая.

·         Квадратичная функция, графиком является парабола.

·         Обратная пропорциональность, графиком является гипербола.

·         Кубическая функция, графиком является кубическая парабола.

      Учитель: Вспоминаем правила построения этих функций. Сейчас каждый из вас построит у себя в тетради одну из перечисленных функций. Функции на вашей карточке  № 1.

Карточки № 1.

Выборочно строим графики функций

 Проверяем построение графиков.

(Учащиеся выборочно показывают свои графики, рассказывают правила их построения и свойства функций).

III.              Объяснение нового материала

Учитель: Давайте попробуем решить уравнение .

(Чтобы всем учащимся было хорошо видно, на стол выкладывается несколько листов формата А4 с записью этого уравнения. Учащиеся будут в затруднение, поскольку уравнения третьей степени они решать не умеют).

Учитель: Мы с вами умеем строить графики функций   и . Подумайте, может быть, с помощью графиков мы сможем решить это уравнение?

(Учащиеся обсуждают возможные варианты, предлагают идеи. Учитель систематизирует  и подводит итог.)

 Учитель: Давайте сформулируем правило решения уравнений графически:

Чтобы решить уравнение графически, надо:

1. Рассмотреть две функции, содержащееся в левой и правой частях уравнения.
2. В одной системе координат построить графики данных функций.
3. Найти точки пересечения этих графиков. Выписать координаты точек пересечения.
4. Абсциссы точек пересечения и есть корни данного уравнения.
5. Записать ответ.

(Учащиеся записывают правило в тетрадь).

Учитель: Скажите, а сколько корней может быть у уравнения?

Ученики: 1, 2, 0, много….

Учитель: Как по графику узнать число корней уравнения?

Учащиеся: Посчитать точки пересечения графиков.

Учитель: Правильно. А теперь каждый из вас возьмёт чистый лист бумаги и в уголках поставит число корней уравнения по графикам предложенных вам схем. Нумеруем уголки листа.

(Учащимся по очереди под номерами предлагаются графические схемы. Учащиеся пишут в уголках число корней и закрывают уголки так, что бы соседи не видели их ответа.)

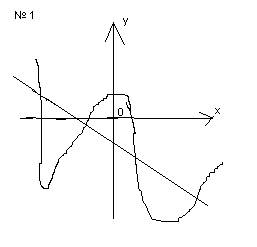
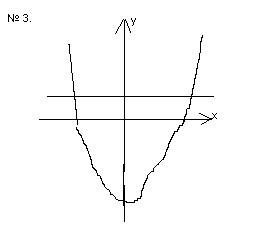
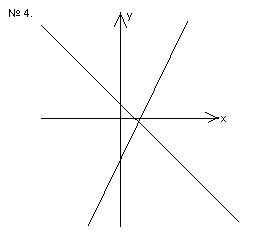
(Учитель, после того, как все учащиеся закрыли свои уголочки. Учитель выкладывает на стол образец правильных ответов. Ребята сверяют свои ответы с шаблоном учителя. Если ответы не совпадают, учитель анализирует ошибку учеников).

Учитель: Сформулируйте правило, как по рисунку найти число корней уравнения.

Ученики: Число корней уравнения соответствует количеству точек пересечения графиков. Если графики не пересекаются, то уравнение не имеет корней. Если графики совпадают, то уравнение имеет бесконечно много корней.

Учитель: А теперь, когда мы знаем правило решения уравнения с помощью графиков, решаем наше уравнение.

(Ученики вместе с учителем решают поэтапно уравнение, проговаривая свойства линейной и кубической функций).

Учитель: Какие ответы у вас получились?

(Ученики озвучивают свои ответы, некоторые из них отличаются десятыми частями).

Учитель: Как вы думаете, почему у вас получились разные ответы?

Ученики: Погрешности построения.

Учитель: Вот мы с вами и пришли ещё к одному выводу: при решении уравнений графическим способом могут получиться неточные ответы.

      А теперь каждый из вас самостоятельно решит предложенное уравнение:

№351,№353,№329
(Учитель помогает и проверяет выполнение задания.)

IV.              Подведение итогов

Что мы сегодня на уроке успели обсудить? (ответы детей)

Тест . ОГЭ. Задание №10.  По графику определить сколько корней имеет уравнение.

Дома прошу вас повторить всё, с чем вы познакомились на уроке, выполнить из учебника

№384(1,3),№385(2)