
Конспект урока по теме « Обобщение и систематизация знаний по теме: « Уравнения» .
Класс: 9 класс
Тип урока: обобщение и систематизация знаний
Цель урока:
1) Повторить теоретический материал по теме.
2) Обобщить и систематизировать знания по теме « Решение уравнений различного вида»;
3) Отработать способы решения уравнений;
4) Развитие логического мышления, памяти, внимания, умения сравнивать и обобщать.
Вид урока: урок-консультация
Планируемые результаты:
Знать определение уравнения, корня уравнения, что такое решить уравнение. Уметь различать типы уравнений, решать различные типы уравнений по алгоритму.
Формы работы: групповая, работа в парах, индивидуальная, работа в тетрадях, работа на учебных сайтах: https://oge.sdamgia.ru/
https://skysmart.ru/
Оборудование: проектор, презентация, опорные конспекты, интернет сайт: https://oge.sdamgia.ru/; https://skysmart.ru/
|
№ |
Этап урока |
Задачи этапа |
Деятельность учителя |
Деятельность ученика |
УУД |
|||
|
личностные |
регулятивные |
Познавательные |
коммуникативные |
|||||
|
1 |
Организационный. Формирование темы урока и целеполагание.( 2 мин) |
Создать благоприятную атмосферу. Настроить детей на работу. Сформулировать тему и цели урока. |
Приветствие.Проверка готовности к уроку. Мотивировать детей на формулирование целей данного урока, обсудив вместе с ними эпиграф к уроку: |
Включаются в работу. Исходя из высказывания формулируют тему и цели урока. Тема: « Решение уравнений» Цели: - обобщить и систематизировать знания по теме урока; - отработать применение способов решения уравнений; - повторить теоретический материал. |
формирование учебной мотивации и целенаправленной познавательной деятельности |
целеполагание |
положительная мотивация к изучению материала |
Планирование сотрудничества с учителем и сверстниками. |
|
2 |
Актуализация знаний. (2 мин) |
Актуализация опорных знаний. Фронтальный опрос. |
Обращается к исторической справке, о происхождении уравнения. Просит сформулировать - что такое уравнение; - что такое корень уравнения; - что значит решить уравнение; Повторяет с классом виды уравнений и алгоритмы их решения. Предлагает заполнить заготовленные таблицы, где нужно распределить уравнения по видам и алгоритму их решения( в приложении). При затруднении заполнения предлагает шаблоны алгоритмами решения и решенными уравнениями. |
Называют определение уравнения, корня уравнения, вспоминают способы решения уравнений, применяют теоретический материал на практике. Работают с предложенными таблицами. Заполняют таблицу по распределению уравнений по видам без решения. При затруднении, используют вспомогательные шаблоны с видами уравнений и алгоритмами решения уравнений.( шаблоны в приложении) |
самоопределение |
умение выполнять поставленную цель |
Анализировать и сравнивать предлагаемые задания |
Выражать свои мысли правильно, анализируя свои и чужие высказывания по теме; научиться работать в паре. |
|
3 |
Закрепление полученных знаний на практике.( 15 мин) |
Обеспечение осмысления материала урока. Выявление пробелов в знаниях. |
Предлагает решить предложенные уравнения, используя известный алгоритм. Предлагает работать в парах и сверять полученные ответы друг с другом . В случае расхождения ответов, свериться с выполненными уравнениями на доске, решение которых контролирует учитель. |
Решают уравнения. Работают в парах. Проверяют решения друг друга и контролируют себя, сравнивая свои решения с решениями на доске. |
Развивать умение выражать свои мысли, внимательно слушать отвечающего. |
Научиться оценивать свою работу, всой вклад в общее дело. |
Научиться выбирать наиболее удачные способы решения уравнения, Узнавать новые способы и учиться их освоить |
Учиться работать в парах , слушать, понимать товарища, тактично и вежливо обращатьс я за помощью и учиться точно и понятно формулировать ответ |
|
4 |
Самостоятельная работа на закрепление изученного материала.(15 мин) |
Выявление качества и уровня овладения знаниями , обеспечение коррекции знаний. |
Предлагает выполнить самостоятельную работу на сайте : Решу ОГЭ https://math-oge.sdamgia.ru/test?id=37439197 Работа рассчитана на выполнение уравнений базового уровня и содержит уравнения повышенного уровня сложности. Просматривает полученные результаты выполнения работы на сайте и фиксирует пробелы в знаниях для последующего разбора ошибок индивидуально , с подбором заданий для отработки.
|
Выполняют самостоятельную работу, перейдя на сайт Решу ОГЭ, используя свои гаджеты. Работают в тетрадях, а ответы заносят в работу на сайте. Выполнив, проверяют свои ответы на сайте и выписывают в тетрадь номера неверно выполненных заданий, чтобы разобрать решение дома. |
Формирование целенаправленной познавательной деятельности |
Учатся контролировать свои действия |
Учатся применять полученные знания в процессе индивидуальной работы. |
Учатся осознавать применяемый алгоритм выполнения с достаточной полнотой. |
|
5 |
Домашнее задание |
Обеспечить понимание при выполнении заданий . |
Предлагает решить работу на сайте СКАЙСМАРТ.РУ https://edu.skysmart.ru/teacher/homework/duruvizolo дополнительное задание второй части ОГЭ по теме: « Уравнения» https://oge.sdamgia.ru/ № 311587,311589 ( с оформлением в тетради)
|
Фиксируют ссылку на работу в тетрадь+ номера классной самостоятельной работы для домашнего разбора решения. |
смыслообразование |
|
|
Умение слушать и понимать других |
|
6 |
Подведение итогов урока. Рефлексия. |
Мотивация собственной деятельности. |
Подведение итогов урока. Самооценка в соответствии с целями урока. Организует обсуждение Какие были цели? Достигнуты ли они? Что получилось, что не получилось? Предлагает заполнить лист самооценки. ( В приложении). |
Делают выводы по уроку, достигнуты цели или нет. Заполняют лист самооценки. |
|
Научиться себя оценивать |
|
Научиться сотрудничать, обосновывать свои суждения по тому или иному вопросу. |
ПРИЛОЖЕНИЕ.
Таблица №1. Распредели уравнения по видам и алгоритмам их решения. В случае, если алгоритм в таблице отсутствует, вспомни план решения уравнения самостоятельно или воспользуйся памяткой.
1) 5х+2=13-7х;
2)
![]() ;
;
3)
![]() ;
;
4)
![]()
5)
![]()
6)
![]()
7) 5(х-4)=3х+8;
8)
![]() ;
;
9)
![]() ;?
;?
10)
![]() ;
;
11)
![]() .?
.?
|
Вид уравнения |
Линейное |
Квадратное |
Дробно-рациональное |
? вспомним, как называется уравнение |
||
|
|
Пример уравнения |
|||||
|
|
ах+в=с; ах=с-в; х=(с-в)/а. |
…
|
Полное кв.ур-е
D=
|
…
|
… |
|
|
… |
||||||
|
|
с(а+х)=в; са+сх=в; сх=в-са; х=(в-са)/с. |
…
|
неполное кв.ур-е
…. |
… |
|
|
|
|
||||||
|
|
Умножим обе части уравнения на в! ах+св=dв; ах=dв-св; х=(dв-св)/а. |
…
|
неполное кв.ур-е
…..
|
|
|
|
|
|
||||||
|
неполное кв.ур-е
|
||||||
|
|
||||||
|
|
|
|
|
|
|
|
![]()
ЛИСТ САМООЦЕНКИ:
Фамилия, Имя_____________________
|
Вид уравнения |
Научился определять этот вид уравнения и решать уравнение |
Не совсем уверенно решаю и определяю вид уравнения |
Не научился определять вид и решать данное уравнение |
|
Линейное |
|
|
|
|
Квадратное полное |
|
|
|
|
Квадратное неполное |
|
|
|
|
Дробно-рациональное |
|
|
|
ПАМЯТКА





Уравнения и системы уравнений.
Справочный материал
1. Уравнения
|
№ п/п |
Вид уравнения |
Схема решения |
|
1 |
Линейные уравнения |
а) раскрыть скобки, б)
перенести известные в правую часть уравнения, неизвестные – в левую (при
переносе через знак равенства менять знаки на противоположные), |
|
2 |
Квадратные уравнения |
а)
раскрыть скобки, 1. полное квадратное уравнение вычислить
дискриминант по формуле D=в2-4ас 2. неполное квадратное уравнение вида ах2+вх=0 Разложить на множители вынесением за скобки и использовать свойство произведения равного 0 3. неполное квадратное уравнение вида ах2+с=0 Решить так: ах2+с=0 ах2=-с
х2=-с:а (в случае, если –с:а<0 – корней нет) д*) выполнить проверку (подставить полученное значение в первоначальное уравнение, при верном решении должно получиться верное равенство). |
|
3 |
Дробно-рациональные уравнения (уравнения, содержащие деление на переменную) |
а)
умножить обе части уравнения на общий знаменатель дробей г) выполнить проверку (подставить полученное значение в первоначальное уравнение, при верном решении должно получиться верное равенство). |
|
4 |
«Другие» |
а)
разложить на множители и использовать свойство произведения, равного 0 -
рассмотреть функции правой и левой частей уравнения - абсциссы точек пересечения – решения уравнения
|
Примечание: если уравнение содержит числовой знаменатель, нужно умножить обе части уравнения на общий знаменатель дробей и решить получившееся уравнение.
2. Задания, сводящиеся к решению уравнений
а) чтобы вычислить координаты точек пересечения графиков функций, нужно составить и решить уравнение, приравняв их левые части, а затем подставить найденное значение в любую из функций и вычислить вторые координаты;
б) чтобы вычислить координаты точек пересечения графика функции с осью абсцисс (х) , нужно приравнять левую часть функции к 0 и решить полученное уравнение.
3. Системы уравнений
1. Способ подстановки:
- выразить из любого уравнения одну из переменных,
-
подставить значение выраженной переменной в другое уравнение,
- решить получившееся уравнение,
- найти значение второй переменной, подставив найденное значение в выражение,
- записать ответ.
2. Способ сложения:
- умножить (при необходимости) одно или оба уравнения системы на такое число, чтобы коэффициенты при одной из переменных в уравнениях стали противоположными числами,
- сложить почленно уравнения, при этом получится уравнение от одной переменной,
- решить получившееся уравнение,
- найти значение второй переменной, подставив найденное значение в одно из уравнений,
- записать ответ.
3. Графический способ:
- выразить в каждом уравнении одну из переменных (чаще всего у) и рассмотреть соответствующие функции,
- в одной системе координат графики этих функций,
- координаты точек пересечения – решения системы,
- записать ответ.
Примечание: если к системе уравнений даны варианты ответов, то легче проверить каждый из вариантов, подставив ответы в систему. Верный ответ, если получается два верных равенства.
РАЗДЕЛ I
1. Уравнения
1. Решите уравнение 3х-х2=0
2. Решите уравнение 3(2+1,5х)=0,5х+24
3.
Решите уравнение ![]() =-3
=-3
4. Решите уравнение 5х2=25х
5. Каждое уравнение, имеющее корни, соотнесите с множеством его корней:
1) х2=х 2) х2=-х 3) х2=-1 4) х2=1
а) 1 и -1 б) 0 и 1 в) 0 и -1
6.
Решите уравнение ![]()
7. Вычислите координаты точек пересечения параболы у=3х2+2 и прямой у=-6х+2
8. Решите уравнение 3х2-27=0.
9.
Решите уравнение ![]()
10.
Найдите корни уравнения ![]()
11. На рисунке изображен график функции у=2х2-4х-6. Вычислите координаты точки А.
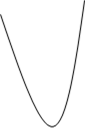 |
![]() у
у
![]() А х
А х
12. Используя графики функций у=х3 и у=-х+2 решите уравнение х3+х-2=0
 у
у
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 13. Какое из
уравнений не имеет корней:
13. Какое из
уравнений не имеет корней:
А. 3х2+5х-2=0 Б. 3х2-10х+6=0 В. 2х2+4х+5=0 Г. 2х2+7х+5=0
14.
2. Системы уравнений
1.
Решите систему уравнений 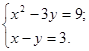
А. (0;3) Б. (0;-3) В. (0;-3),
(3;0) Г. (-3;0), (0;3).
2.
Из данных уравнение подберите второе уравнение системы  так, чтобы она не имела решения
(используйте графические представления)
так, чтобы она не имела решения
(используйте графические представления)
А. у=-х Б. у=х В. у=х2 Г. у=-х2
3.
Решите систему уравнений ![]()
4. Для каждой из систем уравнений укажите число ее решений. (Для ответа используйте графики, график уравнения х2+у2=9 изображен на рисунке)
![]() 1)
1) 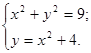 2)
2)  3)
3) 
3

![]() -3
3
-3
3
-3
5.
Используя графики, решите систему уравнений 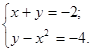
у
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.