Урок по алгебре 9 класс«Решение систем неравенств с одной переменной

Предмет: алгебра 9 класс

Тема: последний урок изучения темы «Решение систем неравенств с одной переменной

Тип урока: урок обобщения изученного материала.

Цели урока:

Образовательные:

• Расширить, обобщить и систематизировать знания о линейных неравенствах и системах линейных неравенств;
• Повторить понятие неравенства, алгоритм решения неравенства с одной переменной и системы неравенств с одной переменной;
• Закрепить свойства, использующиеся при решении неравенств с одной переменной;
• Совершенствовать умения решать неравенства и системы линейных неравенств, графически изображать множество их решений, а также записывать решения в виде числового промежутка.

Развивающие:

• Развивать логическое мышление при установлении связи графического изображения множества решений системы линейных неравенств и записи решения с помощью числового промежутка;
• Развивать навыки самостоятельной работы;
• Развивать монологическую речь в ходе обоснования выполняемых действий;
• Развивать интерес к предмету;
• Расширять общий кругозор.

Воспитательные:

• Воспитывать сознательное отношение к учению;
• Воспитывать познавательную активность учащихся;
• Воспитывать чувство личной ответственности в коллективной работе;
• Воспитывать творческую, всесторонне-развитую личность.

 

Методы обучения: практический, наглядный, словесный.

 

Формы организации деятельности учащихся: фронтальная, индивидуальная, самостоятельная, работа в парах.

 

Оборудование: классная и интерактивная  доска, учебники, тетради, тест, карточки для работы в парах и самостоятельной работы.

 

Структура урока.

1. Организационный момент

 2. Актуализация опорных знаний

а) устная работа по теории;

б) тест.

в) Работа в парах «Найди ошибку».

 3. Историческая справка. Игра «Дешифровщик»

 4. Физкультминутка

 5. Работа у доски

 6. Самостоятельная работа (по вариантам)

 7. Итог урока. Оценки.

 8. Рефлексия. Домашнее задание

 

 

ХОД УРОКА

 

I. Организационный момент.

Вы закончили изучение одной из ведущих тем алгебры 9 класса. И сегодня на уроке вам предстоит обобщить знания об одном математическом понятии этой темы. А поможет вам догадаться, о чем пойдет речь, решение следующего ребуса:

«отрицание» + « = »

Правильно, речь пойдет о неравенстве.

Откройте тетради, запишите число, классная работа и тему урока «Решение систем неравенств с одной переменной».

Итак, сегодня на уроке вы должны обобщить и систематизировать ваши знания о неравенствах с одной переменной и их системах.

 

 

II. Актуализация опорных знаний.

 

А сейчас я предлагаю вспомнить основные теоретические понятия данной темы.

 

А) Работа онлайн викторины triventy.ru

1.  определение линейного неравенства. Приведите примеры
2. Что называется решением неравенства с одной переменной?
3. Что значит решить неравенство с одной переменной?
4. Что называется решением системы неравенств с одной переменной?
5. Что значит решить систему неравенств с одной переменной?
6. Какие свойства, применяются при решении неравенств с одной переменной?

 

Б) Задания теста предполагают ответ «Да» или «Нет». Работа с интерактивной доской.

 

1. Верно ли утверждение: если х > 3 и y > 16, то х + y > 19?

2. Верно ли утверждение: если х > 4 и y > 12, то х · y < 48?

3. Является ли число 0 решением неравенства 5х – 1 < 12?

4. Является ли неравенство 7 х + 10 > 2 х – 5 строгим?

5. Существует ли целое число, принадлежащее промежутку [– 7,5; – 7,3]?

6. Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число, знак неравенства не меняется?

7. Является ли число 3 решением системы неравенств ?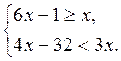

 

8. При любом ли значении параметра а верно неравенство а² + 1 > 0?

 

А теперь давайте проверим, как вы выполнили задание. За каждый правильный ответ учащийся получает 1 балл.

 

Проверка с помощью интерактивной доской: Да, Нет, Да, Да, Нет, Нет, Да, Да.

 

В) Работа в парах

 

Сначала каждый работает с заданием своего варианта, а затем сосед по парте проверяет ответы. За каждый правильный ответ учащийся получает 1 балл.

 

Найди ошибку
7 + 2х > 8; 2х > 8 + 7; 2х > 15; х > 7,5.	7 – 3х < 5; − 3х < 5 + 7; − 3х < 12; х < −4.
х                                     7 Ответ: .	х -1,3 Ответ: k.
2               3                       х   Ответ: .	- 5                              3                    х   Ответ: .

 

 

III. Историческая справка.

 

Из истории математики «О неравенствах» (онлайн-википендия(поиск нужной информации и отбор главного)

Понятие > и < наряду с понятием равенства возникли в связи со счетом предметов и необходимостью сравнивать различные величины. Понятиями неравенства пользовались уже древние греки. Архимед (III в до н.э) указал границы π : .

А вот кто ввел современные знаки неравенств вы узнаете разгадав зашифрованные слова.

 

Задание: решить неравенство. За правильный ответ учащийся получает 1 балл.

 

Вариант 1. 17 - х > 10 - 6х

Вариант 2. 30 + 5х ≤ 18 - 7х

Вариант 3. 6 + х < 3 - 2х  

Вариант 4. 8 + 5у ≤ 21 + 6у

Вариант 5. 3у - 4 > -1 + 6у

Вариант 6. 6а - 1<12 + 7а

 

в	г	а	м	р	р	к	и	о	т
х<1	х>-1,4	х≤-1	у≤-3	х<-1	х<-1	а>13	-13≤у	у≤-1	а>-13

 

и из правильных ответов получили имя английского ученого Гарриот (1560-1621).

 

Историческая справка (поиск информации Онлайн):

 

 В 1631 г. Гарриот ввел поныне употребляемые знаки неравенства. Он рассуждал так:

•        если два числа не равны, напоминающий знак параллельности нарушается, и тогда отрезки будут пересекаться, то есть иметь общую точку как слева, так и справа;

•        если отрезки имеют общую точку слева, то это знак меньше;

•        если два отрезка имеют общую точку справа, то это знак больше.

            По сей день мы пользуемся этими знаками.

 

Задание: решить систему неравенств. За правильный ответ учащийся получает 1 балл.

 

 

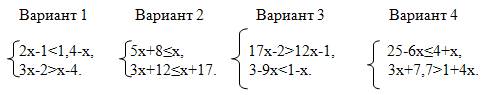
Б	А	У	Г	М	Е
(-1; 0,8)	х<-1	х≤-2	(0.2; 0,25)	х>-1,4	[ 3; 6.7)

 

 

Из правильных ответов получим имя французского математика Пьера Буге (1698-1758)

 

Историческая справка:

 

В теории и практических задачах встречаются знаки неравенства, соединенные со знаком равенства «не меньше» или «не больше». Как вы знаете, такие неравенства называются нестрогими в отличие от неравенств, содержащих знак > или < и называемых строгими. Эти символы были введены в 1734 году французским математиком Пьером Буге.

 

 

V. Работа у доски.

Сколько целых чисел являются решениями системы неравенств:

 

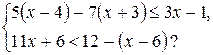
Решение.

 

1)   5(х - 4) – 7(х + 3) ≤ 3х – 1;           2) 11х + 6 < 12 – (х - 6);

5х – 20 – 7х – 21 ≤ 3х – 1;                 11х + 6 < 12 – х + 6;

5х – 7х – 3х ≤ -1 + 20 + 21;               11х + х < 12 + 6 – 6;

-5х ≤ 40;                                              12х < 12;

х ≥ - 8.                                                  х < 1.

 

3)

 

х = -8, -7, -6, -5, -4, -3, -2, -1, 0, 1. 10 штук.

 

Ответ. 10.

 

VI. Самостоятельная работа.

 

 

 

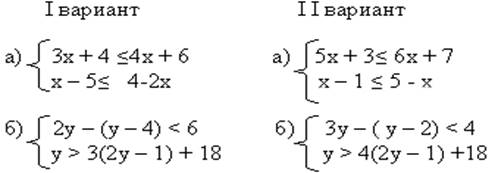
VII. Итоги урока.

 

- Итак, урок наш подошел к концу. Пора подводить итоги. Сегодня на уроке вы закрепили такие важные понятия как неравенство с одной переменной и системы неравенств, узнали новые факты из истории, связанные с этим понятием. Вы все хорошо поработали, и я надеюсь, получили большое удовольствие.

 

А теперь каждый может сам оценить свою работу на уроке. Подсчитайте общее количество баллов, которое вы заработали на уроке.

 

Если количество набранных вами баллов попадает в отрезок от 12 до 20, то вы смело можете поставить себе "5";

Если сумма ваших баллов принадлежит полуинтервалу от 8 до 12, включая 8, то ваша оценка "4";

Если же вы набрали количество баллов из интервала от -1 до 8, то вам надо еще поработать над этой темой, а итоговую оценку я поставлю только после того, как проверю вашу самостоятельную работу.

 

VIII. Домашнее задание.

 

- А теперь, домашнее задание

Повторить п.6 №191,№186

Рефлексивный этап.

Что именно вы повторили на уроке?

Составить свою систему уравнений –знаний по данной теме .

 

- Спасибо за плодотворную работу. Желаю всем удачи и благодарю за урок. До свидания.