Урок на тему Линейное уравнение с двумя переменными"

Урок №
ТЕМА: Линейное уравнение
с двумя переменными

Ход урока

I. Устная работа.

1. Какие из следующих уравнений являются линейными
с двумя переменными?

а) 5xy + 3 = 7;                     в) y – x = 10;                  г) 7x –  = 5;

б) 3x – 7y = ;                   г) 5x + 2x² = 1;               е) –4x + 0,8y = –2.

В линейных уравнениях назовите коэффициенты a, b и с.

2. Решением какого уравнения является пара чисел ?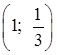

а) 2x + y = 1;                   в) x + 2y = 2;

б) x – y = ;                       г) x – 3y = 0.

II. Объяснение нового материала.

На этом уроке следует разобрать, как в линейных уравнениях выражать одну переменную через другую и как с помощью этого можно находить решения таких уравнений. также нужно рассмотреть вопрос о решении уравнений в целых числах.

1. Выражение одной переменной через другую.

Сначала необходимо актуализировать знания учащихся, задав им следующие вопросы:

– Какие два уравнения называются равносильными?

– Будут ли уравнения 3х = 9 и 2х = 6 равносильны?

– Какие преобразования можно совершать при решении линейных уравнений с одной переменной?

– Поясните каждое из проводимых преобразований на примере решения уравнения 1 – 2х = 5.

Затем сообщить учащимся, что уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной, а значит, при их решении можно выполнять аналогичные преобразования. Благодаря этому появляется возможность выражать в таких уравнениях одну переменную через другую.

Примеры:

а) х + 2y = 4.

Выразим переменную х через у:

х = 4 – 2y.

Выразим переменную у через х:

2у = 4 – х;

у = .

б) 3х – 5y = 2.

3х = 2 + 5y;               –5y = 2 – 3х;

х = .               y = .

2. решение линейных уравнений с двумя переменными.

Замечаем, что с помощью выражения одной переменной через другую можно находить разнообразные решения линейных уравнений с двумя переменными. Рассмотреть по учебнику решение уравнения 5x + 2y = 12. Ещё раз сделать вывод о том, что подобные уравнения могут иметь бесконечно много решений.

3. решение уравнений в целых числах.

Учащиеся уже разобрали, как решаются линейные уравнения с двумя переменными, и выяснили, что они могут иметь бесконечно много решений. Среди всех решений есть пары, включающие в себя дробные числа.

Однако при решении некоторых задач возникает необходимость отыскать только целые или натуральные пары решений уравнений с двумя переменными. Рассмотреть пример решения такой задачи из учебника.

III. Формирование умений и навыков.

Основная цель на этом уроке состоит в том, чтобы учащиеся научились в линейных уравнениях с двумя переменными выражать одну переменную через другую и отыскивать решения таких уравнений.

К решению задач на составление уравнений можно перейти только в том случае, если данное умение будет сформировано в полной мере.

1. № 1030.

2. № 1032.

Решение:

а) 3х + 2у = 12.

    2у = 12 – 3х;

    у = ;

    у = 6 – 1,5х;

если х = 2,       то у = 6 – 1,5 · 3 = 3                (2; 3);

если х = –4,     то у = 6 – 1,5 · (–4) = 12          (–4; 12);

если х = 10,     то у = 6 – 1,5 · 10 = –9            (10; –9).

3. № 1035.

4. № 1036.

Решение:

Пусть было взято х двухрублёвых и у пятирублёвых монет. Получим уравнение:

2х + 5у = 28.

Требуется найти все пары натуральных значений переменных х и у, удовлетворяющих этому уравнению.

Выразим переменную х через у:

2х = 28 – 5у;

х = .

Имеем:

если у = 2, то х = 9;

если у = 4, то х = 4.

Других пар натуральных чисел, удовлетворяющих уравнению 2х + 5у = 28, нет.

Ответ: 4 или 9 монет.

5. № 1038.

Решается аналогично предыдущей задаче.

№ 1042 (можно предложить сильным учащимся выполнить дополнительно).

Решение:

Пусть п – некоторое натуральное число. Если оно при делении на 5 даёт остаток 1, то справедливо следующее равенство:

п = 5q + 1, где q – частное от деления на 5.

Аналогично можно записать равенство:

п = 6p + 2, где р – частное от деления на 6.

Получим уравнение:

5q + 1 = 6p + 2;

5q – 6p = 1.

Выразим переменную q через переменную р:

5q = 6p + 1;

q = .

Нужно подобрать наименьшую натуральную пару (p; q), удовлетворяющую уравнению.

Если р = 4, то q =  = 5. Найдем п:

п = 5q + 1 = 5 ∙  5 + 1 = 26.

Ответ: 26.

IV. Проверочная работа.

Вариант 1

1. Решением каких уравнений является пара чисел (–2; 3):

а) 2x + y = 1;                      в) x² + y = 1;

б) x – y = –5;                      г) 3x + y² = 3?

2. Выразите из уравнения 2x – 3y = 7 переменную х через у и найдите три решения этого уравнения.

Вариант 2

1. Решением каких уравнений является пара чисел (1; –4):

а) 2x + y = –2;                     в) 2x² + y = –2;

б) x – y = –3;                       г) 4x – y² = –7?

2. Выразите из уравнения 5x + 2y = 3 переменную у через х и найдите три решения этого уравнения.

V. Итоги урока.

– Какие уравнения называются линейными с двумя переменными?

– Что называется решением уравнения с двумя переменными?

– Какими свойствами обладают уравнения с двумя переменными?

– Как  можно  найти  решение  линейного  уравнения  с  двумя  переменными?

– Сколько  может  иметь  решений  линейное  уравнение  с  двумя  переменными?

Домашнее задание: № 1031, № 1034, № 1035, № 1037.

Дополнительно: № 1041.