Урок на тему Рациональные неравенства"

У р о к  №8/1

ТЕМА:Рациональные неравенства
(4 ч)

Цели: ввести понятие рационального неравенства с одной переменной; закрепить знание трех правил (из § 1) при решении рациональных неравенств; научить применять метод интервалов к решению рациональных неравенств.

Ход урока

I. Проверочная работа (10–12 минут).

2. Найдите область определения выражения f(х):

II. Объяснение нового материала.

1. Определение рационального неравенства с одной переменной.

Рациональное неравенство с одной переменной х – это неравенство вида h(х) > q(х), где h(х) и q(х) – рациональные выражения.

2. При решении рациональных неравенств используются те три правила, которые были сформулированы выше в § 1 (повторить эти правила).

3. При  решении  рациональных  неравенств  используют  метод интервалов.

4. Учитель объясняет решение № 2.1 (а; б).

а) (х + 2)(х + 3) > 0. Рассмотрим выражение f(х) = (х + 2)(х + 3). Оно обращается в 0 в точках – 2; – 3; отметим эти точки на числовой прямой:

Числовая прямая разбивается указанными точками на три промежутка, на  каждом  из  которых  выражение  f(х) сохраняет постоянный знак. Найдем знаки выражения на каждом промежутке: на промежутке (–∞; –3) f(х) > 0; на промежутке (– 3; – 2) f(х) < 0; на промежутке (– 2; ∞) f(х) > 0. Неравенство f(х) > 0 выполняется на промежутках (–∞; – 3) и (– 2; +∞).

О т в е т: х < – 3; х > – 2.

б) (х + 3)(х – 0,5) < 0.

Выражение f(х) = (х + 3)·(х – 0,5) обращается в нуль в точках – 3 и 0,5:

На промежутке (–∞; – 3) выражение f(х) > 0; на промежутке (– 3; 0,5) выражение f(х) < 0; на промежутке (0,5; + ∞) f(х) > 0. Выбираем промежуток, на котором выражение отрицательно.

О т в е т: – 3 < х < 0,5.

III. Закрепление изученного материала.

1. Решить № 2.2 (а; б) на доске и в тетрадях.

а) t(t – 1) < 0;  t = 0;  t = 1

О т в е т: 0 < t < 1.

б) t(t – )(t – 12) ≥ 0;  t = 0;  t = ; t = 12

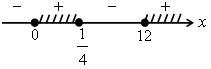
О т в е т: 0 ≤ t ≤ ; t ≥ 12.

2. Решить № 2.3 (в; г) с комментированием на месте.

в) х2 – 3х ≥ 0;  х(х – 3) ≥ 0;  х = 0;  х = 3

О т в е т:  х ≤ 0;  х ≥ 3.

г) 5х + х2 < 0;  х(5 + х) < 0;  х = 0;  х = – 5

О т в е т: (– 5; 0).

3. Решить № 2.4 (в; г), используя формулу а2 – b2 = (а – b)(a + b).

4. Решить № 2.6 (в; г). Учитель объясняет решение № 2.6 (в).

в) (х – 2)(х + 3)(х + 1) < 0. Нули выражения f(х) = (х – 2)(х + 3) × (х + 1) равны 2; – 3 и – 1. Отметим эти числа на числовой прямой:

О т в е т: (– ∞; – 3); (– 1; 2).

г) (х + 5)(4х + 1)(х – 3) > 0;  х = – 5; – 0,25; 3.

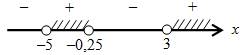
О т в е т: – 5 < х < – 0,25;  х > 3.

5. Решить № 1.15, закрепляя ранее изученный материал.

3х2 – 2рх – р + 6 = 0

а) Квадратное уравнение имеет два различных корня, если D > 0.

D = (– 2р)2 – 4 · 3(– р + 6) = 4р2 + 12р – 72;

4р2 + 12р – 72 > 0;

4р2 + 12р – 72 = 0;

р2 + 3р – 18 = 0;

р1 = 3;

р2 = – 6

4р2 + 12р – 72 = 4(р – 3)(р + 6); с помощью метода интервалов решим неравенство 4(р – 3)(р + 6) > 0:

О т в е т: при р  < – 6 и  р > 3.

б) Квадратное уравнение имеет один корень, если D = 0:

4р2 + 12р – 72 = 0;

р1 = – 6;

р2 = 3.

О т в е т: при р  = – 6 и  р = 3.

в) Квадратное уравнение не имеет корней, если D < 0:

О т в е т: при – 6 < р < 3.

IV. Итоги урока. Выставление отметок.

Домашнее задание: изучить материал на с. 13–16 учебника и записать в тетради решение примеров 1 и 2; решить № 2.1 (в; г), № 2.2 (в; г), № 2.3 (а; б); № 2.4 (а; б), № 2.5 (а; б).