
Публикация является частью публикации:
План-конспект проведения урока.
Алгебра 9 класс.
Учитель: Рогозина А.В.
Тема: «Решение неравенств методом интервалов».
Тип урока: комбинированный.
Цели и задачи урока:
-образовательные - повторить алгоритм решения неравенств второй степени методом
интервалов, формировать навыки применения этого алгоритма в нестандартных
ситуациях;
-развивающие – развивать логическое мышление, способность самостоятельно решать
учебные задачи;
-воспитательные – прививать интерес к предмету, знакомить с медиаресурсами на
уроках математики, развивать сознательное восприятие учебного материала
Оборудование:
- мультимедийный проектор;
- компьютер с необходимым программным обеспечением;
- раздаточный материал (карточки).
1
Чтобы все на уроке прошло без заминки,
Его мы начнем…
Ну, конечно с разминки!
12 в квадрате?
Можно ли при умножении чисел получить 0?
Наименьшее натуральное число?
Первая координата точки?
Что
больше ![]() или 2
или 2 ![]() ?
?
Третья часть от 60?
Наибольшее целое отрицательное число?
Корень
уравнения x![]() = - 9?
= - 9?
____________________________________________________________
2
Проверка домашнего задания.
Взяли в руки карандаши,
Плюсы и минусы ставить спеши.
№ 332 (а)
![]()
Область определения данной функции вытекает из условий, что подкоренное выражение должно быть неотрицательным, т.е.
(5-х)(х+8)≥ 0
(х-5)(х+8) =0, выделим функцию
Нули функции: (х-5)(х+8) =0
х1 =5; х2 = - 8
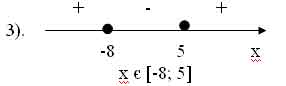
область определения данной функции: [-8;
5]
Ответ: [-8; 5]
_____________________________________________________________
1) (х+2)(х-3)(х+5)>0 2) (х-7)(х+5)≤0

-5 -2 3 х -5 7 х
Ответ: ( - 5; - 2 )![]() ( 3;
( 3;![]() ) Ответ:
[ - 5; 7]
) Ответ:
[ - 5; 7]
______________________________________________________
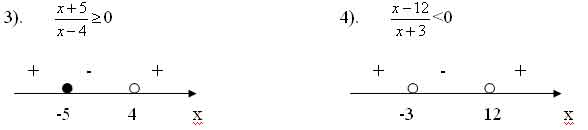
Ответ:
(- ![]() ; - 5]
; - 5]![]() ( 4; +
( 4; +![]() ) Ответ:
( - 3; 12).
) Ответ:
( - 3; 12).
________________________________________________________
3
А теперь необычное задание,
Требует знания и понимания.
На пример внимание направьте,
Найдете ошибку – исправьте!
1) ( x – 1)( x + 5 )( x – 2 ) > 0
Ответ:
( 1; 2 )![]() ( 5; +∞).
( 5; +∞).
2)( x + 2 )( x – 7 )( x + 4 ) ≤ 0
Ответ: [ - 4; - 2 ]![]() [ 7; + ∞).
[ 7; + ∞).
3)![]() < 0
< 0
Ответ: [ - 3; - 1] ![]() [ 4; +).
[ 4; +).
4
Сегодня на уроке мы повторяем и закрепляем тему «Решение неравенств». Какой же самый простой способ решения неравенств вы знаете? (Презентация)
Выполните самостоятельную работу (по 1 примеру каждый – номера примеров написаны на карточках).
Поменяйтесь тетрадями и проверьте решение своего соседа.
Верните тетради обратно. Переверните карточки с буквами и сверьте свой ответ. Если ответ совпал, поднимите букву.
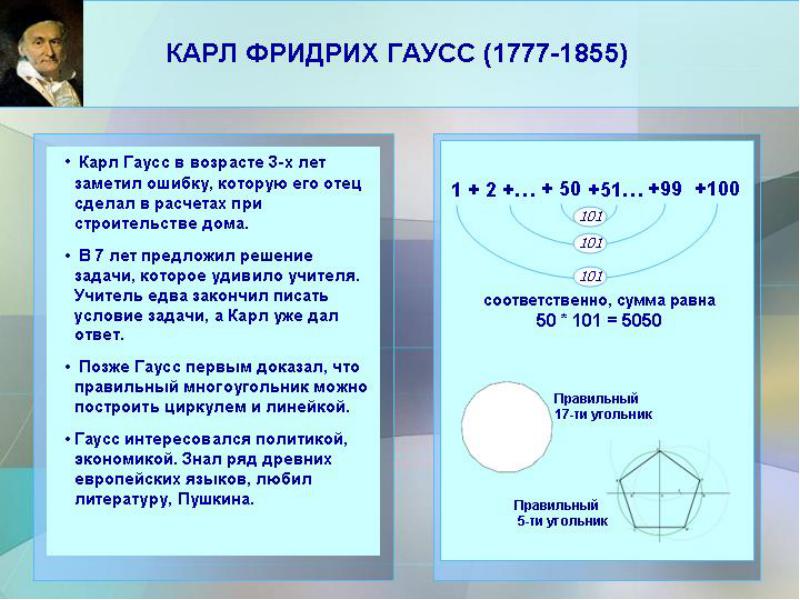
Какое слово получилось? Да, Карл Фридрих Гаусс – выдающийся немецкий ученый.
Историческая справка. (Слайд)
__________________________________________________________
5
Ну а сейчас, ребята, стоп –
Математический калейдоскоп!
Кто в терминах не знает затрудненья,
Напишет все без промедленья.
Продолжите формулу:
x2 – y2=
(аn)m =
(x + y)2 =
( аb )k =
D =
_______________________________________________________________
6
Наша Настя в подсказке не ошиблась ни разу,
Мы даём ей право продолжить фразу:
1) Неравенством 2 степени с одной переменной называется …
2) Если у квадратичной функции а<0, то ветви параболы направлены…
3) В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции …
4) Чтобы изобразить схематически параболу, нужно найти…
5) При решении числовых неравенств знак не меняется, если …
6) При делении обеих частей неравенства на отрицательное число, знак неравенства …
7) Решить неравенство, значит найти все его…
_______________________________________________________________
7
Нелегкий вопрос – то,
Но ведь одному:
Все сложно и просто,
Считай по уму!
1. Сумма противоположных чисел.
2. Как называется равенство, верное при любых допустимых значениях переменной?
3. Угол, на который поворачивается солдат «кругом».
4. Два числа, отличающиеся только знаком.
5. Самый удобный и универсальный способ решения неравенств?
6. Как называется выражение, записанное с помощью знаков > или < ?
__________________________________________________________________
8
Вы внимательно глядите,
Есть ошибки - удалите:
МАТИМАТЕКА КОЭФИЦИЕНТ НЕРАВИНСТВО
АДНОЧЛЕН ВЫРОЖЕНИЕ ЗНАК
ЕДЕНИЦА ПЕНПЕНДИКУЛЯР КВАДРАД
_________________________________________________________________
9
Подведение итогов.
1).Какая задача стояла перед нами в начале урока?
Можно ли считать, что мы ее решили.
2).Повторите алгоритм решения неравенств методом интервалов.
______________________________________________________
10
Задание на дом.
Учебник «Алгебра-9» под редакцией С.А.Теляковского.2008г.
Повторить §6,
№389 (б), № 390 (б), №393(б), №394(б).
Используемая литература.
1).Учебник «Алгебра 9», 2008 под редакцией Теляковского.
2).Сборник заданий для подготовки к итоговой аттестации в 9 классе
–«Алгебра»,автор Л.В.Кузнецова.
3).«АЛГЕБРА - 9» - проверочные и контрольные работы, автор Т.А.Капитонова.
4).»Алгебра -9 класс» - дидактические материалы, автор Ю.Н.Макарычев.
Карл Фридрих Гаусс (1777-1855) — немецкий математик, астроном, геодезист и физик.
Карл Гаусс родился 30 апреля 1777, Брауншвейг, ныне Германия.
Скончался 23 февраля 1855, Геттинген, Ганноверское королевство, ныне Германия).








Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.