Урока на тему „Перпендикулярность прямых и плоскостей” (бизнес-игра) 10 класс

Урока на тему „Перпендикулярность прямых и плоскостей” (бизнес-игра) 10  класс

Данный урок является обобщающим по теме, организуется работа по решению задач исследовательского характера.

ХОД УРОКА

I. Организационный момент.

На доске записана тема урока, которую учитель объявляет и объясняет правила бизнес-игры.

Ученики класса объединяются в команды, каждая с которых — это правление определенного банка; капитан команды — это президент банка, члены команды — правление банка. Название каждого банка представлена табличкой на столе: банк «Аваль», банк «Омега», «Интербанк», «Мегабанк»,

Президент имеет право решающего голоса в случае, когда мысли членов правления банка не совпадают.

               II. Приобретение начального капитала.

Командам по очереди предлагают вопросы и задачи. Если ответ правильный, то баллы суммируются, если нет — баллы вычитаются и купить этот вопрос или задачу может другой банк, но уже по цене на один балл меньше.

1. Вопросы для устного опроса. (по 3 вопроса для каждой команды)

(Каждый вопрос оценивается в 5 баллов.)

1.                 Определение перпендикулярности прямой и плоскости.

1.                 Признак перпендикулярности прямой и плоскости.

2.                 Теорема о трех перпендикулярах.

3.                 Определение перпендикулярности плоскостей.

4.                 Признак перпендикулярности плоскостей.

5.                 Расстояние от точки до плоскости.

6.                 Расстояние от прямой до плоскости.

7.                 Расстояние между параллельными плоскостями.

8.                 Перпендикуляр к плоскости.

9.                 Расстояние между скрещивающимися прямыми.

10.            Наклонная и проекция.

11.            Свойства наклонных.

Учитель заполняет таблицу полученных баллов.

2. Задачи для устного решения.

(Каждая задача оценивается в 10 баллов.)

1.     Известно, что SO I (ABC), SA = SB ∆ABC — прямоугольный.

Объяснить размещение точки А.

2. Известно, что ABCD— прямоугольник, КА ┴(ABC). Где на рисунке отрезок, длину которого можно считать расстоянием от точки К к С В?

3. Известно, что SO┴(ABC), SP = SN = SK. Объяснить размещение точки А.

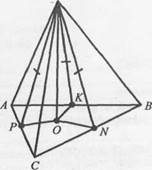
4. Известно, что KB ┴ (ABC), ∆ABC - прямоугольный. Объяснить, почему КС является расстоянием от точки К до АС.

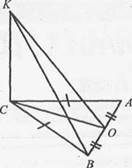
5.Известно, что KC┴(ABC), ∆ABC – равнобедренный. Объяснить, почему КО есть расстоянием от точки К к АВ

III. Аукцион задач.

Учитель выставляет задачу, как лот, на торги. Представитель банка, которые быстрее ее решит, поясняет решение возле доски. Задачи оцениваются 1,3 в 5 баллов, задача 2 — в 10 баллов.

Задача 1. Расстояние от точки М ко всем вершинам квадрата равна 5 см. Найти расстояние от точки М к плоскости квадрата, если диагональ квадрата 6 см.

Задача 2. Отрезок ВМ перпендикулярный к плоскости прямоугольника ABCD. Доказать, что прямая CD перпендикулярна к плоскости МВС.

Во время оформления и подготовки решения задачи одним учеником на доске, остальные ученики выполняют логическую задачу.

Задача 3. (Логическая.) Какой квадрат лишний?

IV. Решения задач.

Каждый ученик команды получает задачу и лист на котором строит рисунок и решает задачу. Задачи подбираются соответственно к уровню обученности учеников.

1.                 Постройте изображения куба АВСDА₁В₁С_ИD₁ и запишите грани куба, которые перпендикулярные к плоскости А₁АС . (З балла)

2.                 Дан прямоугольный треугольник АВС с гипотенузой АВ. К плоскости треугольника АВС проведен перпендикуляр ВМ. Найдите величину угла МСА. (З балла).

3.                 К плоскости квадрата АВСD проведен перпендикуляр SВ. Найдите величину угла SАD. (З балла).

4.                 Точка М находится на одинаковом расстоянии от всех сторон правильного треугольника со стороной 12 см и удалена от плоскости треугольникa на 2 см. Найдите расстояние от точки М до сторон треугольника. (3 балла).

5.                 Каждое ребро треугольной пирамиды равно а. Найдите расстояние между двумя ребрами, которые являются скрещивающимися (3 балла).

Ответ.1. ABCD и А₁В₁С_ИD₁ , 2.< МСА=90, 3. <SАD=90 , 4. 4 см , 5. а/√2.

Учитель раздает аналогичные задачи каждой команде, ученики их решают и сдают на проверку. Учитель проводит обсуждение решения этих задач и привлекает к этому учеников.

Каждый ученик получает баллы за решенную задачу и эти баллы добавляются к баллам команды.

V. Итог урока.

По количеству набранных баллов определяют банк-победитель. (анализируется количество баллов в таблице).

Работу всех участников игры учитель оценивает по их участию в решении задач.

Скачано с www.znanio.ru