Векторы в пространстве. Компланарные и некомпланарные векторы. Разложение вектора по трем некомпланарным векторам.

План урока по геометрии

Класс: 10

Дата:

Тема: Векторы в пространстве. Компланарные и некомпланарные векторы. Разложение вектора по трем некомпланарным векторам.

Цели  урока:

• повторить, как находятся координаты вектора, длина вектора;
• закрепить навыки в использовании формул при решении задач координатно-векторным методом;
• проверить умения и навыки применять эти знания при решении задач.

Ход урока

Организационный момент.

Сообщить тему урока и его цель.

Актуализация опорных знаний.

Индивидуальная работа по карточкам у доски.

Карточка № 1.

Дано: А (-3; 4; 1), В (5; -2; -3).

Составьте задачу по этим данным и решите ее.

Карточка № 2.

Дано: А (-1; 2; 2), В(1; 0; 4), С(3; -2; 2).

Составьте задачу по этим данным и решите ее.

(К карточке № 1 можно подобрать следующие задания:

Найти:

а) длину отрезка АВ;

б) координаты вектора ;

в) координаты середины отрезка АВ;

г) длину вектора , где М – середина отрезка АВ, О – начало координат;

д) угол между векторами  и ;

е) площадь треугольника АОВ;

ж) среднюю линию треугольника АОВ и т. д.)

Обучающийся сам поставит себе задачу, которую способен выполнить. Задача оценивается в зависимости от степени трудности выбранного задания.

Презентация с устными заданиями.

Слайд 1. Распознай формулы:

а) ;

б) x₁x₂+y₁ y₂+z₁z₂;

в) {; };

;

(От невнимательности многие дети не видят ошибки в этой формуле.)

д) cos=;

е) cos= .

Слайд 2. Дано:  = 2, || = 5.

Найдите скалярное произведение векторов  и , если:

а) векторы  и  сонаправлены;

б) векторы  и  противоположно направлены;

в) векторы  и  перпендикулярны;

г) угол между векторами  и  равен 60º;

д) угол между векторами  и  равен 120º.

Слайд 3. Дано: А (-3; 1; 2), В (1; -1; 2).

Найти:

а) координаты середины отрезка АВ;

б) координаты и длину вектора АВ.

Слайд 4. Найдите скалярный квадрат вектора 7

Слайд 5. Вычислите скалярное произведение векторов  и , если {1; 2; 3},

{-1; -2; -3}.

Слайд 6. Дан квадрат АВСD. Найдите угол между векторами:

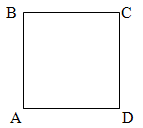
а)  и ;

б)  и ;

в)  и

Проверка выполненных заданий по карточкам.

(Обратить внимание на решение задач разными способами.)

Напиши мне письмо.

На столах у обучающихся карточки с координатами двух или трех точек. Каждая карточка адресована определенному ученику. Задача ученика, получившего карточку, написать задание с предложенными данными для указанного товарища.

Решение задач.

Задача № 1.

Точки А(-1; 3), В(2; -1), С(2; 2) являются вершинами треугольника АВС с биссектрисой ВК. Найдите 16АК.

Решение.

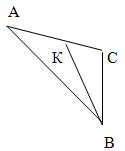
1. ВК – биссектриса, тогда  =  или =

2. ВС = ² +  = 3.

АВ =  = 5.

 = , т. о., АК = АС.

3. АС =  = .

4. 16 АК² = 16, 16 АК² = 16    10 =  = 62,5.

Ответ. 16 АК² = 62,5.

Задача № 2.

(Выполняется наиболее подготовленным учеником на переносной доске. Чертеж и условие задачи приготовлены заранее.)

В прямоугольном параллелепипеде АВСDА₁В₁С₁D₁ АВ=1, ВС=2, ВВ1=3. Вычислите косинус угла между прямыми АС и D₁В.

Дано: АВСDА₁В₁С₁D₁ – прямоугольный параллелепипед, АВ=1, ВС=2, ВВ₁=3.

Найти:

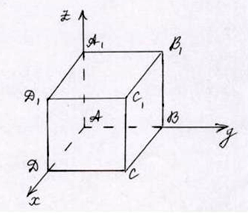
Решение.

Введем прямоугольную систему координат Ахуz.

АВ=1, ВС=2, ВВ₁=3, тогда А(0; 0; 0), В(0; 1; 0), С(2; 1; 0), D1(2; 0; 3).

, .

 = .

cos( =  =  = .

Ответ.  =

Те, кто продолжат свое обучение в вузе, встретятся с таким разделом математики, как «Векторная алгебра». При изучении этой темы вам пригодятся знания, полученные в школе по теме «Метод координат».

Задача № 3.

Точка М является серединой стороны АВ в треугольнике с вершинами А(3; -2; -8), В(1; -4; -4), С(-1; -3; -3). Найти: 1) угол ВСМ; 2) площадь треугольника АВС.

Решение.

1. Найдем координаты точки М.

= ; = ; = ; М(2; -3; -6).

2. Найдем ВСМ. =

{2; -1; -1}, {3; 0; -3}.

   = 2 (-1)  = 9.

|  =

  =

 =  = , ВСМ = 30º.

 {4; 1; -5}.

АВС =

 =  -   +=-6-6-6.

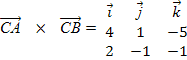АВС =  =  = 6.

Ответ. ВСМ = 30º, SАВС = .

Самостоятельная работа.

Вариант 1.

1. Дано: , ;

а) || = 4, || = 3, ()= 30º;

б)  ,  = 3 + 2.

Найти:   .

2. Дано: А(1; 1; 2), В(0; 1; 1), С(2; -2; 2), D(2; -3; 3).

Найдите угол между прямыми АВ и СD.

3. Дано: А(0; 4; 0), В(2; 0; 0), С(4; 0; 4), D(2; 4; 4).

Доказать: АВСD - ромб.

Вариант 2.

1. Дано: , ;

а) ,  = 6 + 8;

б) || = 2, || = 5, ()= 60º.

Найти:   .

2. Дано: А(1; 1; 0), В(3; -1; 0), С(4; -1; 2), D(0; 1; 0).

Найдите угол между прямыми АВ и СD.

3. Дано: А(0; 1; 2), В(; 1; 2), С(; 2; 1), D(0; 2; 1).

Доказать: АВСD - квадрат.

Итог урока.

Какое задание из классной и самостоятельной работы вам показалось самым трудным, какое самым легким (при наличии времени попросить обучающихся обосновать свой выбор).

Домашнее задание.

Карточки для д/з «Напиши мне письмо».

Карточка № 1.

Дано: А (-4; 3; 1), В (2; -1; 3).

Карточка № 2.

Дано: А (-1; -2; 2), В(-1; 0; 4), С(3; -2; -2).

Карточка № 3.

Дано: А (2; -5; 3), В(-4; 0; -1), С(-2; -3; 5).

Карточка № 4.

Дано: А (3; -4; -3), В (-5; 2; 1).

Поделиться…