Возведение в степень произведения и степени

               Возведение в степень произведения и степени

Вспомнив переместительное и сочетательное свойства умножения, мы с помощью примера показываем, как возвести произведение в степень, и формулируем правило. Аналогично, на примере выясняем, как возвести степень в степень, и также формулируем правило. В конце урока решаем примеры для закрепления полученных знаний на практике.

Конспект урока "Возведение в степень произведения и степени"

Вопросы занятия:

·  повторить переместительное и сочетательное свойство умножения;

·  на примере показать, как возвести произведение в степень;

·  сформулировать правило возведения произведения в степень.

Материал урока

Прежде, чем приступить к изучению нового материала, вспомним, что:

Также вспомним переместительное и сочетательное свойства умножения.

А теперь давайте преобразуем выражение:

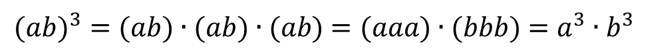
Вообще, для любых чисел а и b и натурального числа n верно равенство:

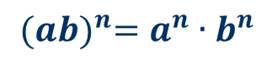
Таким образом, можем сформулировать определение.

Чтобы возвести в степень произведение, нужно каждый множитель возвести в эту степень и результаты перемножить.

Например,

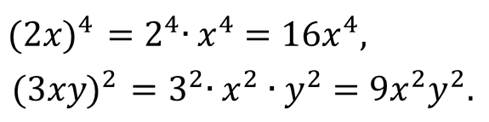
Следует также отметить, что свойство степени произведения распространяется на степень трёх и более множителей.

А теперь разберёмся с возведением степени в степень. Для этого рассмотрим выражение, которое представляет собой степень, основание которой само является степенью.

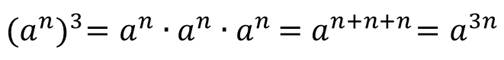
Вообще, для любого числа а и произвольных натуральных чисел m и n верно равенство:

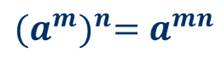
Сформулируем определение.

При возведении степени в степень основание оставляют прежним, а показатели степеней перемножают.

Например,

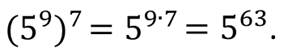
Пример.

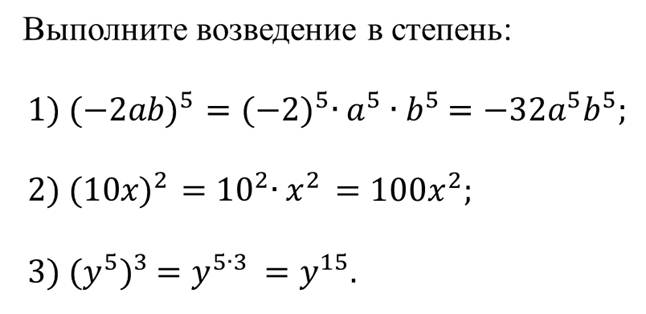
Пример.