Поделиться
ВЫЧИСЛЕНИЕ УГЛА МЕЖДУ ПРЯМЫМИ.docx
ГБПОУ ВО «Воронежский техникум строительных технологий»
МЕТОДИЧЕСКОЕ ПОСОБИЕ
по дисциплине
Элементы высшей математики
ВЫЧИСЛЕНИЕ УГЛА МЕЖДУПРЯМЫМИ.
УСЛОВИЯ ПАРАЛЛЕЛЬНОСТИ И ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМЫХ
Воронеж
2022
Рассмотрено на заседании ПЦК естественнонаучных дисциплин
Протокол № _____ от _____________
Председатель ПЦК _______ Болычева Т.В.
Разработана на основе Федерального государственного образовательного стандарта среднего профессионального образования для специальности 09.02.07 Элементы высшей математики
Настоящее пособие предназначено для студентов 2 курса ГБПОУ ВО «Воронежский техникум строительных технологий» специальности «Информационные системы» и полностью соответствует программе по математике для СПО. Оно может быть использовано студентами для самостоятельного изучения раздела программы, а также преподавателем на уроке при изучении нового материала, для домашнего задания, при повторении и подготовке к зачётной работе.
Пособие включает в себя, помимо задач, теоретические сведения, необходимые для решения задач раздела «Аналитическая геометрия», справочный материал, подробные решения типовых примеров, а также упражнения для самостоятельного решения.
Автор - составитель: Сафонова Елена Артуровна, преподаватель ГБПОУ ВО
«Воронежский техникум строительных технологий»
ВЫЧИСЛЕНИЕ УГЛА МЕЖДУ ПРЯМЫМИ.
УСЛОВИЯ ПАРАЛЛЕЛЬНОСТИ И ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМЫХ
1. Прямые заданы общими уравнениями
Пусть
прямые 
заданы общими уравнениями, то есть
.
Их
нормальными векторами будут 
Обозначим
угол между прямыми 
через
, а угол между их
нормальными векторами - 
.
Возможны 2 случая:
1) 
2) 
Если 
то 
Если 
то 
.
Но в
любом случае 
. Значит, 
.
Запишем эту формулу через координаты
нормальных векторов 
и 
.
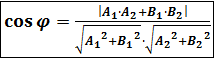(1)
а) Прямые 
параллельны тогда и только тогда, когда
векторы 
и 
коллинеарны, то есть 
или
или 
.
б) Прямые 
перпендикулярны тогда и только тогда,
когда векторы
и 
перпендикулярны, то есть 
или
2. Прямые заданы уравнениями с угловыми коэффициентами
Пусть прямые заданы уравнениями с угловыми коэффициентами:
, где 
и 
Возможны два случая.
2)
0
0
(внешний
угол треугольника равен 
сумме двух внутренних не смежных с ним).
Но
в любом случае 
. Значит 
(2)
а) Если прямые 
и
параллельны, то 
и
- условие параллельности прямых
б)
Если прямые 
и
перпендикулярны, то 
и 
не существует, то
есть знаменатель дроби (2) 
или
- условие перпендикулярности прямых
3. Прямые заданы каноническими уравнениями
Пусть прямые 
и
заданы каноническими уравнениями, то есть
и 
.
Их направляющие
векторы 
и 
.
Возможны два случая.
1)
2) 
0
0
Если 
Если 
Но в любом случае
. Таким образом, получаем
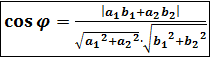(3)
а)
Прямые
и
с направляющими векторами 
и 
параллельны, когда векторы
коллинеарны, то есть
- условие параллельности прямых
б)
Прямые
и
перпендикулярны, если перпендикулярны
их направляющие векторы, то есть 
или
- условие перпендикулярности прямых
РЕШИТЬ ЗАДАЧИ
1. Найдите углы наклона прямых: а) 
2. Дано
уравнение прямой 
Найти величину угла этой прямой с
положительным направлением оси абсцисс.
3. Вычислить угол
между прямыми: а) 
и 
б)
и 
, в) 
и 
.
4. Найдите
углы наклона прямых: а) 
б) 
5.
Вычислите угол между прямыми 
и 
.
6. Вычислите угол
между прямыми: а) 
и 
б) 
и 
7.
Установить, параллельны ли прямые: а) 
и 
;
б) 
и 
в) 
и 
.
8. Установить,
перпендикулярны ли прямые: а) 
и 
б) 
и 
9.
При каком значении 
прямые 
и 
параллельны?
10. При
каком значении 
прямые 
и 
перпендикулярны?
11. Вычислите
угол между прямыми: 
и 
.
12.
Вычислите угол между прямыми: 
и 
13.
Вычислите угол между прямыми: 
и 
.
14.
При каком значении прямые 
и 
параллельны?
15.
Через точку пересечения прямых 
и 
проведена прямая, параллельная прямой 
Найдите её
уравнение.
Литература
1. Богомолов Н.В. Самойленко П.И. Математика: Учебник. - М.: Дрофа, 2010.
2. Дадаян А.А. Сборник задач по математике. Учебное пособие. Гриф МО РФ, – М.: ФОРУМ: ИНФРА – М, 2013.
3. Зимина О.В. Линейная алгебра и аналитическая геометрия. Учебный комплекс М.: Издательство МЭИ.2006.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
