Занятие 2. Исследование модели степенной функции

Занятие 2 к программе факультатива «Решение исследовательских задач в программе GeoGebra»

Занятие 2. Исследование модели степенной функции

Задача на построение. Построить модель графика степенной функции.

Пошаговое построение.

1. Создайте целочисленный слайдер n (-5; 5) и действительный слайдер

k (-5; 5).

2. В командной строке введите: y = k * x ^ n. В панели объектов появится

функция f (x), а на графическом полотне отобразится ее график.

Учебное исследование 1. Изменяя значение обоих слайдеров, наблюдайте за изменениями графика. Сделайте выводы о виде графика при n <0, n = 0, n = 1, n> 1. Поставьте в свойствах слайдера n шаг на значение 0,1. Как выглядит график при дробной степени n? Как влияет на вид графика параметр k?

Выводы. Графики степенной функции при натуральном показателе n> 1 называются параболами порядка n. Примеры отдельных случаев:

n = 1 - прямая, ГMT на плоскости при x = y;

n = 2 - парабола; n = 3 - кубическая парабола.

При n = {2,4,6,8, ...} график функции y = хⁿ представляет собой параболу. при –k график инвертируется - ветви «смотрят» вниз.

При n = {3,5,7,9, ...} график функции y = хⁿ представляет собой кубическую параболу.

При -k график инвертируется - отображается относительно оси Оу.

Чем больше n, тем круче ветви графика идут вверх и вниз, и больше приближаются к оси Оу, и тем медленнее удаляются от оси Ох на промежутке (-1,1). Чем больше | k |, тем ближе ветви графика к оси Оу.

Графики функций вида y = xⁿ , где n <0 - натуральное число, называются гиперболами порядка n. Гипербола бесконечно приближается к осям, но никогда не пересекает их.

При n = {- 2, 4, 6, ...} ветви гиперболы располагаются в I и II четвертях.

При n = {- 3, 5, -7, ...} ветви гиперболы располагаются в I и III координатных четвертях.

Чем меньше n, тем ветви графика быстрее приближаются к оси Ох и медленнее - до Оу. Чем больше k, тем больше ветви графика удаляются от осей. При -k график инвертируется - отображается относительно начала координат.

При дробных значениях n в следующих случаях график степенной функции принимает следующий вид:

0 <n <1 - ветвь параболы, обратной к у = хⁿ (I четверть).

1> n - ветвь параболы у = хⁿ (I четверть).

n <0 - ветвь гиперболы у = х^-n (I четверть).

Другие частные случаи:

n = 0 - y = x0 -> y = 1 - прямая, параллельная Ох, проходящей через y = 1;

k = 0 - график у = 0 принимает вид прямой, совпадающей с осью Ох.

Учебное исследование 2. Почему в приведенном ниже изображении графики функций с различными степенями, которые накладываются друг на друга, образуют «пучки» в трех точках?

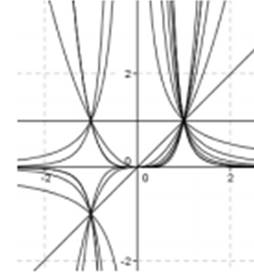
Характеристики параболы у = хⁿ , N = {2,4,6,8, ...}:

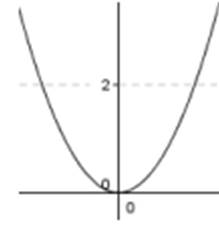
1. Область определения: х ∈ (-∞; + ∞). Область значений: у ∈ [0; + ∞).

2. Функция парная.

3. Функция возрастает при х ∈ [0; + ∞) убывает при х ∈ (-∞, 0].

4. Функция вогнута при х ∈ (-∞; + ∞). Точек перегиба нет.

5. Асимптот нет.

6. Функция равна нулю при х = 0.

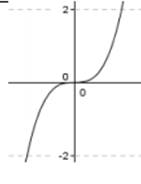
Характеристики кубической параболы у = хⁿ , N = {3,5,7,9, ...}:

1. Область определения: х ∈ (-∞; + ∞). Область значений: у ∈ (-∞; + ∞)

2. Функция нечетная.

3. Функция возрастает при: х ∈ (-∞; + ∞).

4. Функция выпуклая при х ∈ (-∞, 0] и вогнутая при х ∈ [0; + ∞).

Точка (0; 0) является точкой перегиба.

5. Асимптот нет.

6. Функция равна нулю при х = 0.

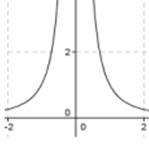
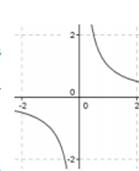
Характеристики гиперболы у = х^-n:

1. Область определения: х ∈ (-∞; 0) U (0; + ∞). Область значений: у ∈ (0; + ∞) по четной степени; в ∈ (-∞; 0) U (0; + ∞) по нечетной степени.

2. Функция нечетная.

3. Нечетная степень убывает на промежутке х ∈ (-∞; 0) U (0; + ∞) при четной степени - возрастает при х ∈ (-∞; 0) и приходит при х ∈ (0; + ∞).

4. При нечетной степени функция выпуклая при х ∈ (-∞; 0); при нечетной степени - функция вогнута при х ∈ (-∞; 0) U (0; + ∞). Точек перегиба нет.

5. Горизонтальной асимптотой является прямая y = 0, вертикальной - прямая х = 0.

Скачано с www.znanio.ru