Занятие 3. Исследование графика показательной функции

Занятие 3 к программе факультатива «Решение исследовательских задач в программе GeoGebra»

Занятие 3. Исследование графика показательной функции

Задача на построение. Построить модель графика показательной функции.

Пошаговое построение.

1. Создайте действительный слайдер a (-5; 5) с шагом 0,1.

2. В командной строке введите: y = a ^ x. В панели объектов появится функция f (x), а на графическом полотне отобразится ее график.

Учебное исследование 1. Изменяя значение слайдера, наблюдайте за изменениями вида графика. Сделайте выводы о виде графика при всех возможных значениях а. Сформулируйте выводы и характеристики графика показательной функции. Убедитесь, что график всегда проходит через точку (0,1) при любых значениях а.

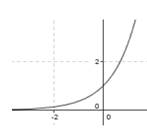
При 0 <а <1 график функции - монотонно убывающая кривая, при a> 1 - монотонно возрастающая.

При а = 1 график представляет собой прямую y = 1 при х (-∞; + ∞).

При а = 0 график - прямая у = 0 при х≥0.

Графики фукций y = a^x и y = a^x  симметричны относительно оси Оу.

График всегда находится в I и II координатных четвертях - то есть, всегда будет иметь область значений y> 0 - независимо, к какой степени приведена переменная а.

Примечание. Чтобы увидеть график экспоненциальной функции, нужно ввести в командную строку уравнение: а = е. Число е необходимо выбрать из списка математических символов справа от командной строки (значок α).

Характеристики показательной функции у = ах

1. Область определения: х ∈ [-∞; + ∞). Область значений: в ∈ [0; + ∞).

2. Функция общего вида.

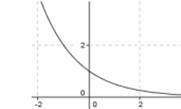
3. При 0 <a <1 функция убывает на всей области определения; при a> 1 возрастает на всей области определения.

4. Функция вогнута при х ∈ (-∞; + ∞). Точек перегиба нет.

5. Горизонтальной асимптотой является прямая y = 0.

Скачано с www.znanio.ru