Занятие 4. Исследование графика логарифмической функции

Занятие 4 к программе факультатива «Решение исследовательских задач в программе GeoGebra»

Занятие 4. Исследование графика логарифмической функции

Задача на построение. Построить модель графика логарифмической функции.

Пошаговое построение.

1. Создайте действительный слайдер a (0, 5) с шагом 0,1.

2. В командной строке введите: y = log (a, x). В панели объектов появится функция f (x), а на графическом полотне отобразится ее график.

Учебное исследование 1. Изменяя значение слайдера, наблюдайте за изменениями графика. Сделайте выводы о виде графика при всех возможных значениях а. Сформулируйте характеристики графика логарифмической функции. Почему при а = 1 график логарифмической функции не отображается?

Выводы. Согласно определению логарифма, уравнение log₁x = b равносильно уравнению 1^b = x, следовательно х может принимать только значение 1. Поэтому b является неопределенной величиной.

График логарифмической функции всегда проходит через точку (1,0) при любых значениях а.

Логарифмическая функция является обратной к показательной функции     y = a^x, следовательно, ее график является симметричным графику показательной функции по одной и той же основой относительно прямой y = x - биссектрисы первого и третьего координатных углов.

Функция всегда имеет область определения > 0.

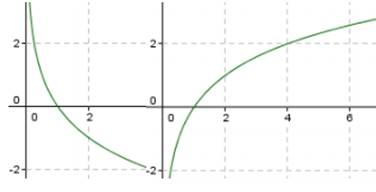
Характеристики логарифмической функции y = logaх.

1. Область определения: х ∈ [0; + ∞). Область значений: в ∈ (-∞; + ∞).

2. Функция общего вида.

3. Функция приходит на всей области определения при 0 <a <1 и растет на всей области определения при a > 1.

4. Функция вогнута на промежутке х ∈ (0; + ∞) при 0 <a <1 и выпуклая на промежутке х ∈ (0; + ∞) при a> 1. Точек перегиба нет.

1.     Вертикальной асимптотой является прямая х = 0.

Скачано с www.znanio.ru