Занятие 5. Исследование графика тригонометрической функции.

Занятие 5 к программе факультатива «Решение исследовательских задач в программе GeoGebra»

Занятие 5. Исследование графика тригонометрической функции.

Задача на построение. Построить модели графиков тригонометрических функций.

Пошаговое построение.

1. В командную строку введите: y = sin(x). На графическом полотне отобразится график заданной функции.

2. Постройте графики для всех описанных выше тригонометрических функций.

Примечание: при построенных графиках синуса и косинуса производные от них функции можно создать, непосредственно указав их отношение.

Например, для функций p (x) = sin x и q (x) = cos x график функции тангенса можно построить так: t (x) = p (x) / q (x)

Задайте для каждого графика разные цвета и создайте флажки для контроля их видимости.

Учебное исследование 1. Для каждой функции создайте слайдеры коэффициентов. Например, для графика синуса добавьте коэффициенты a, b и c: y = a * sin (b * x + c). Наблюдайте за изменениями графиков функций, изменяя значение слайдеров. Убедитесь, что параметр а определяется как амплитуда функции. По определению, амплитуда - это наибольшее значение, которое принимает определенная величина, изменяющаяся по гармоническому закону (в данном случае, тригонометрическая функция), а параметр b определяет период функции Т.

Характеристики графика функции y = sin х.

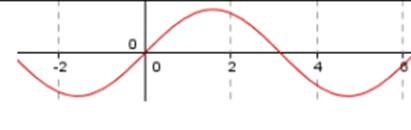
1. Область определения: х ∈ (-∞; + ∞). Область значений: у ∈ [-1; 1].

2. Функция нечетная.

3. Период функции: T = 2π.

4. Функция убывает при, возрастает при .

5. Функция вогнута при, выпуклая при, выпуклая при . Координаты точек перегиба: .

6. Функция поворачивается к нулю при x = πk.

7. Асимптот нет.

Характеристики графика функции y = cos х.

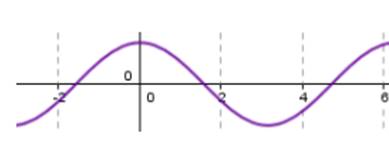
1. Область определения: х ∈ (-∞; + ∞). Область значений: у ∈ [-1; 1].

2. Функция парная.

3. Период функции: T = 2π.

4. Функция убывает при , возрастает при .

5. Функция вогнута при , выпуклая Координаты точек перегиба: .

6. Функция возвращается к нулю при x = π / 2 + πk.

7. Асимптот нет.

Характеристики графика функции y = tg х.

1. Область определения: х ∈ (-∞; + ∞) \ (π / 2 + πk). Область значений: у ∈ (-∞; + ∞).

2. Функция нечетная.

3. Период функции: T = π.

4. Функция возрастает на всей области определения.

5. Функция вогнута при , выпуклая

 при

Координаты точек перегиба: (πk; 0).

6. Функция возвращается к нулю при x = πk.

7. Асимптот нет.

Характеристики графика функции y = ctg х.

1. Область определения: х ∈ (-∞; + ∞) \ (π + πk).

область значений: у ∈ (-∞; + ∞).

2. Функция нечетная.

3. Период функции: T = π.

4. Функция приходит на всей области определения.

5. Функция вогнута при , выпуклая при

. Координаты точек перегиба: (π / 2 + πk; 0).

6. Функция поворачивается к нулю при x = π / 2 + πk.

7. Асимптот нет.

Скачано с www.znanio.ru