Как определить местонахождения острова, корабля, точки?

Как определить местонахождения острова, корабля, точки?

(Педагогическая мастерская).

Урок математики 6 класс (Координатная плоскость).

Разработала Елена Вячеславовна Морозова,

учитель математики МБОУ СОШ № 2 г.Гулькевичи

Цель: изучить и сформировать знания по теме «Декартова система координат», научить определять координаты точки на плоскости, по координатам отмечать, строить точки; развивать самостоятельность и коллективизм при изучении нового материала, творчество и аккуратность.

Оборудование: мультимедийный проектор, ПК, презентация.

У каждого ученика – линейка, карандаш, ластик, ручка, тетрадь с печатной основой, рабочая тетрадь.

На группу – лист миллиметровой бумаги, лист в клетку, набор раздаточного материала.

Ход урока.

1.Организационный момент.

Класс делится на группы по 5-6 человек, в группах определяются: командир – руководитель, секретарь – ведет записи, экспедитор – получает задание для группы, советник – читает задания, художник – летописец. Группы рассаживаются за отдельные столы.

2. Индукция. Учитель читает:

1)    Фрагмент Ж. Верн «Таинственный остров» стр 122-123

 (Тут Гленарван снова взял перо и, не колеблясь, написал следующее: "7 июня 1862 года  трехмачтовое  судно  "Британия",  из  порта  Глазго, затонуло у берегов Патагонии в Южном  полушарии.  Два  матроса  и  капитан Грант попытаются достичь берега, где окажутся в плену у жестоких индейцев. Они бросили этот  документ  под...  градусами  долготы  и  37°11'  широты. Окажите им помощь, или они погибнут".

2)Расчерчивается два поля размером 8×8 клеток, каждый из двух игроков, слева сверху вниз нумеруются строки от 1 до 8, сверху буквами обозначаются столбцы, на одном поле расставляются «корабли» 4 по 1 клетке, 3 по 2 клетке, 2 по 3 клетке, 1 по 4 клетки; второе поле остается пустым для изображения «кораблей» противника. Игроки определяют клетки буквой и цифрой, определяют попадание по кораблю или промах и т.д. выигрывает тот игрок, который первым потопит корабли противника.

3)Чтобы попасть в нужную вам точку надо пройти 20 шагов вперед, а

затем повернув направо пройти ещё 10шагов.

Ребята! Какие чувства, ассоциации у вас возникли?

(Тема на экране, учащиеся записывают в тетрадь)

3. Подготовительная работа.

1) В тетради с печатной основой № 88.

Каждая точка с целочисленными координатами обозначена буквой. Например, точка с координатами (0;0) есть А, (2,1) – точка Ж, Ч(-1;2).

Задание:

- расшифруйте запись:

(-1;-2), (2;-3)

(-2;-3), (1;-1), (0;1), (1,-1), (-1;0), (-2;0), (0,-2)

(Ты молодец)

- зашифруйте слово «математика»

 ( (-2;-3), (0;0), (-1;-2), (-2;0), (-2;-3), (0;0), (-1;-2), (0;2), (-1;1), (0;0))

2) В тетради с печатной основой № 89. «Ломоносов о математике». Прочтите при помощи ключа зашифрованный текст. Вы узнаете, что сказал великий русский ученый М.В. Ломоносов о математике. (Указание-пояснение. В зашифрованном тексте 7 слов, каждая строка – слово, две цифры в квадратике – буква (например, 2,5 – п; 3,1 – т; 1,3 - г)

(Химия – правая рука физики, математика её глаз)

4. Изучение нового материала.

1) Изучите в группах справочную и историческую информацию.

Справочная информация.

Абсцисса (лат. abscissus) – отсечённый.

Ордината (лат. ordinatus) – упорядоченный.

Координаты (лат. coordinatus: co – вместе, совместно, ordine – упорядоченный) – заданные совместно и в определённом порядке числа, определяющие положение точки на плоскости в заданной системе координат.

Исторические сведения:

Термины абсцисса и ордината  были введены в XVII веке Лейбницем.

Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также - декартова система координат.

2)    В рабочих тетрадях: провести через точку О две взаимно перпендикулярные прямые х и у – оси координат. Ось ОХ (обычно горизонтально) – ось абсцисс, а ось ОУ – ось ординат. Точка О - начало координат. Стрелочкой отмечается положительное направление. Выберем единицу отсчёта.

А(х;у) – точка А имеет координаты х;у.

Плоскость разбита на 4 четверти.

5. Закрепление.

1) Задание для группы.

Карта «Острова Сокровищ».

Определить координаты точек:  А – мыс добра, В – дерево, Р – крепость, К – клад, Д – место встречи, С – мыс Надежды, М – бухта Знаний и запишите их в тетради.

2) № 1393. Начертить в тетрадях декартову систему координат, отметить начало координат, единичные отрезки, отметить точки по заданным координатам.

3) В тетради с печатной основой № 92.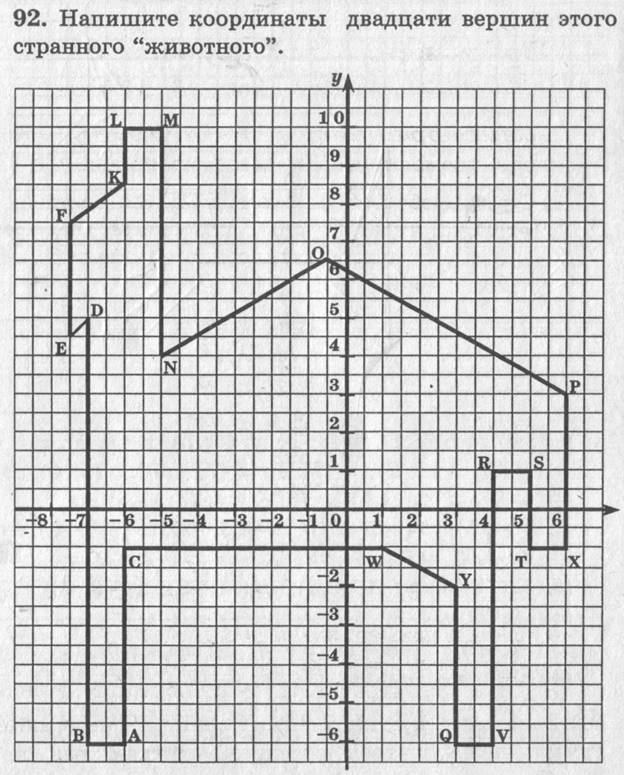  

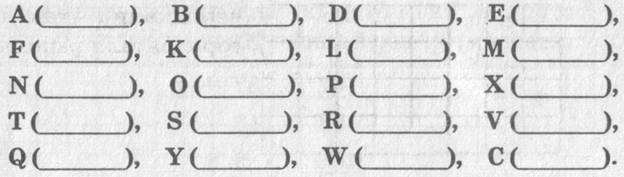 Каждому члену группы заполнить координаты точки одной строки (4 точки). Взаимопроверка парами между группами.

6. Проверка знаний. Творческое задание (работа группы). На листе миллиметровой бумаги построить декартову систему координат, отметить начало координат, за единичный отрезок выбрать 1см, по заданным координатам построить точки, соединив  их по очереди отрезками.

1 группа: (1;-3), (2;-3), (3;-2), (3;3), (4;3), (5;4), (5;6), (4;7), (3;7), (2;6), (3;5), (3;5,5), (4;5), (3;4), (2;5), (-3;5),

(-4;6), (-4;9), (-5;10), (-5;11), (-6;10), (-7;10), (-7;10), (-7;8), (-9;8), (-9;7), (-8;6), (-6;6), (-7;3), (-6;2), (-6;-1), (-7;-2), (-7;-3), (-6;-3), (-4;-2), (-4;2), (1;2), (2;-1),

 (1;-2), (1;-3) (собака)

2 группа:  7,5;5), (-4;7), (-3;7), (-3;9), (1;1), (3;0), (5;-0,5), (7;-4), (7;-8), (10;-5), (13;-3), (17;-2), (19;-2), (17;-3), (14;-7), (7;-9), (6;-10), (2;-10), (2;-9), (5;-9), (3;-8), (1,5;-6), (0,5;-3),(0,5;-10),(-2,5;10), (-2,5;-9), (-1;-9), (-1;-3), (-3;-10), (-6;-10), (-6;-9), (-4,5;-9), (-3;-4), (-3;0,5), (-4;3), (-5;3),

(-7,5;4), (-7,5;5) (лиса)

3 группа: (-14;2), (-12;4), (-10;5), (-8;10), (-7;11), (-8;5), (-7;4), (-5;1), (-3;1,5), (3;0), (8;1), (10;0), (11;2), (12;1), (12;0), (11,5;-1), (13;-5), (14;-4,5), (15;-9),

(15;-11), (13,5;-6,5), (11;-8), (8;-5), (-1;-7),

(-5;-6), (-7;-7), (-9;-7), (-11;-6,5), (-13;-7), (-15;-6), (-12;-5,5), (-9;-6), (-11;-1),

(-13;0), (-14;2) (заяц)

4 группа:  (-2;2), (-2;-4), (-3;-7), (-1;-7), (1;4), (2;3), (5;3), (7;5), (8;3), (8;-3),

(6;-7), (8;-7), (10;-2), (10;1), (11;2,5),(11;0), (12;-2), (9;-7), (11;-7), (14;-2), (13;0), (13;5), (14;6), (11;11), (6;12), (3;12), (1;13), (-3;13), (-4;15),(-5;13),

 (-7;15), (-8;13), (-10;14), (-9;11), (-12;10), (-13;9), (-12;8),(-11;9), (-12;8),

(-11;8), (-10;7), (-9;8),(-8;7), (-7;8), (-7;7), (-6;7), (-4;5), (-4;-4),

(-6;-7), (-4;-7), (-2;-4),

глаз (-7;11)  (лось)

5 группа: (-6;-1), (-5;-4), (-2;-6), (-1;-4), (0;-5), (1;-5), (3;-7), (2;-8), (0;-8), (0;-9), (3;-9), (4;-8), (4;-4), (5;-6), (8;-4), (8;0), (6;2), (4;1), (0;1), (-2;2), (-6;-1), (-10;-2), (-13;-4), (-14;-7), (-16;-9), (-13;-7), (-12;-10), (-13;-14), (-10;-14), (-10;-13),

(-9;-13), (-10;-9), (-5;-9), (-5;-15), (-2;-15), (-2;-13), (-2;-10), (-1;-10), (-1;-11),

 (-2;-13), (0;-15), (2;-11). (2;-9) и (0;-2) и (4;-2) (слон)

7. Подведение итогов.

Защита своей работы. В каждой группе – рисунок животного. Собираем зоопарк.

8. Домашнее задание. В тетради с печатной основой № 88(б), 90(а); творческое задание – на листочке в клеточку нарисовать рисунок, построить систему координат, определить координаты точек рисунка.