«Комплексные числа и действия над ними. Геометрическая интерпретация комплексных чисел»

Тема урока: «Комплексные числа и действия над ними. Геометрическая интерпретация комплексных чисел» группа АЭС3

Тип урока: Урок систематизации знаний (общеметодологической направленности).

Цель урока: включить новую информацию в структуру прежних знаний; расширить сведения студентов о числах; научить распознавать виды комплексных чисел; научить действиям с комплексными числами в алгебраической форме.

Формирование УУД:

·        познавательных: научить студентов структуризации полученного знания, развивать умение перехода от частного к общему и наоборот, научить видеть каждое новое знание, повторить изученный способ действий в рамках всей изучаемой темы; научить обобщению, развивать умение строить теоретические предположения о дальнейшем развитии темы, научить видению нового знания в структуре общего курса, его связь с уже приобретенным опытом и его значение для последующего обучения.

·        коммуникативных и личностных: умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в пару со сверстником и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.

·        регулятивных: умение обрабатывать информацию и ранжировать ее по указанным основаниям; формировать коммуникативную компетенцию студентов; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.        

Формы работы студентов: Фронтальная, индивидуальная.

Организация деятельности студентов на уроке:

• Самоопределение.
• Актуализация знаний и фиксирование затруднений.
• Постановка учебной задачи, целей урока.
• Составление плана, стратегии по разрешению затруднения.
• Реализация выбранного проекта.
• Этап самостоятельной работы с проверкой по эталону.
• Этап рефлексии деятельности.

Оборудование урока: проектор, доска, раздаточный материал.

Структура урока:

1.     Самоопределение (3 мин.)

2.     Актуализация знаний и фиксирование затруднений (5 мин.)

3.     Постановка учебной задачи, целей урока (2 мин.)

4.     Реализация выбранного проекта (18 мин.)

5.     Этап самостоятельной работы с проверкой по эталону (10 мин.)

6.     Этап рефлексии деятельности (2 мин.)

Ход урока:

1.     Самоопределение.

Преподаватель приветствует студентов и начинает урок с высказывания Платона. Задается вопрос: О чем мы поговорим на нашем уроке сегодня? Студенты отвечают: о числах. Преподаватель задает вопрос: Что такое число? Студенты отвечают: Число — абстракция, используемая для количественной характеристики объектов.

2.     Актуализация знаний и фиксирование затруднений.

Методический прием "Интеллектуальная разминка". На слайде изображены различные числа, студентам необходимо ответить на вопрос "Что пропущено"?

1,2,3,.... - натуральные числа,

-3,-2,-1,0,1,2,3,… - целые числа,

,,- рациональные числа,

,,- действительные числа.

Пропущены комплексные числа.

3.     Постановка учебной задачи, целей урока.

Студенты записывают тему урока со слайда.

4.     Реализация выбранного проекта.

Студенты отвечают на вопрос: Какие числа называются комплексными?

Комплексными числами (слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. образующих единое целое) называются числа вида a + bi , где a и b – действительные числа, а число i , определяемое равенством        

называется мнимой единицей . 

Рассмотрим  квадратное уравнение x² = – 1. Оно  на множестве действительных чисел решений не имеет, так как среди действительных чисел нет такого числа, квадрат которого отрицателен.

Таким образом, действительных чисел явно недостаточно, чтобы построить такую теорию квадратных уравнений, в рамках которой каждое квадратное уравнение было бы разрешимо. Это приводит к необходимости расширять множество действительных чисел до множества, в котором было бы разрешимо любое квадратное уравнение. Такое множество называется множеством комплексных чисел и обозначается С.

Мы пришли к введению понятия мнимой единицы  i=_.  Т.е. множество действительных чисел расширяется до множества комплексных чисел  за счет мнимой единицы.

Студенты записывают информацию со слайда.

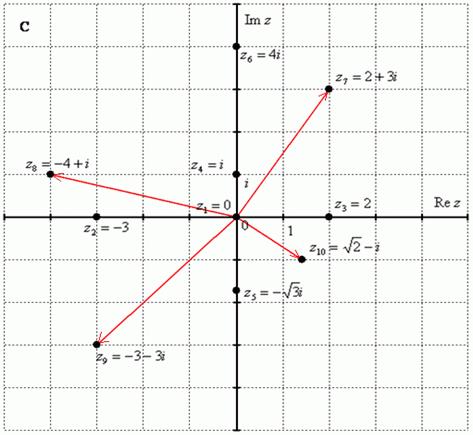
Геометрическая интерпретация комплексных чисел.

•         Плоскость называется комплексной, если каждому комплексному числу                   ставится в соответствие точки плоскости с координатами              ,причем, это соответствие взаимно-однозначное (рис. 1).

•         Ось        называется действительной осью, т. к. на ней расположены точки, соответствующие числам, у которых         .

•         Ось       называется мнимой осью, т. к. на ней расположены точки, соответствующие числам, у которых           .

•         Таким образом, любое комплексное число              можно изобразить  на плоскости точкой с координатами         , причем взаимно однозначно.

Действия с комплексными числами:

ü при сложении (вычитании) комплексных чисел соответственно складываются (вычитаются) их действительные и мнимые части.

Пример 1

Сложить два комплексных числа  Z₁=2+5i  Z₂=4-3i

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:    Z=6+2i

Пример 2

Найти разности комплексных чисел и, если,  Z₁=10-25i  Z₂=1-3i

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Z=10-25i  -(1-3i)=9-22i

ü чтобы перемножить два комплексных числа необходимо перемножить их как многочлены, учитывая, что i² = -1.

Пример 3

Найти произведение комплексных чисел   Z₁=1-i    Z₂=3+6i   Ответ: Z=9+3i

ü При выполнении деления комплексных чисел числитель и знаменатель дроби умножают на число, комплексно - сопряженное знаменателю дроби

Пример 4    Найти   =

(Умножаем  числитель и знаменатель на  (4 -i))  

5.     Этап самостоятельной работы с проверкой по эталону.

Студенты по очереди выходят решать примеры у доски:

1.     Сложить два комплексных числа  Z₁=-4+10i    Z₂=5+3i  

Ответ: Z=1+13i

2.     Найти разность комплексных чисел  Z₁=-5+10i    Z₂=1+3i

Ответ: Z=-6+7i

3.     Найти произведение комплексных чисел Z₁=5-2i    Z₂=1-4i  

Ответ: Z=-3-22i

4.    Найти 

Ответ:

6.     Этап рефлексии деятельности.

• Мне больше всего удалось…
• Для меня было открытием то, что …
• За что ты можешь себя похвалить?
• Что на твой взгляд не удалось? Почему? Что учесть на будущее?
• Мои достижения на уроке...

• Мне больше всего удалось…
• Для меня было открытием то, что …
• За что ты можешь себя похвалить?
• Что на твой взгляд не удалось? Почему? Что учесть на будущее?
• Мои достижения на уроке...

• Мне больше всего удалось…
• Для меня было открытием то, что …
• За что ты можешь себя похвалить?
• Что на твой взгляд не удалось? Почему? Что учесть на будущее?
• Мои достижения на уроке...

• Мне больше всего удалось…
• Для меня было открытием то, что …
• За что ты можешь себя похвалить?
• Что на твой взгляд не удалось? Почему? Что учесть на будущее?
• Мои достижения на уроке...

1.     Сложить два комплексных числа  Z₁=2+5i  Z₂=4-3i

2.     Сложить два комплексных числа  Z₁=-4+10i    Z₂=5+3i  

3.     Найти разность комплексных чисел Z₁=10-25i  Z₂=1-3i

4.     Найти разность комплексных чисел  Z₁=-5+10i    Z₂=1+3i

5.     Найти произведение комплексных чисел   Z₁=1-i    Z₂=3+6i

6.     Найти произведение комплексных чисел Z₁=5-2i    Z₂=1-4i  

7.   Найти 

8.    Найти 

1.     Сложить два комплексных числа  Z₁=2+5i  Z₂=4-3i

2.     Сложить два комплексных числа  Z₁=-4+10i    Z₂=5+3i  

3.     Найти разность комплексных чисел Z₁=10-25i  Z₂=1-3i

4.     Найти разность комплексных чисел  Z₁=-5+10i    Z₂=1+3i

5.     Найти произведение комплексных чисел   Z₁=1-i    Z₂=3+6i

6.     Найти произведение комплексных чисел Z₁=5-2i    Z₂=1-4i  

7.   Найти 

8.    Найти 

1.     Сложить два комплексных числа  Z₁=2+5i  Z₂=4-3i

2.     Сложить два комплексных числа  Z₁=-4+10i    Z₂=5+3i  

3.     Найти разность комплексных чисел Z₁=10-25i  Z₂=1-3i

4.     Найти разность комплексных чисел  Z₁=-5+10i    Z₂=1+3i

5.     Найти произведение комплексных чисел   Z₁=1-i    Z₂=3+6i

6.     Найти произведение комплексных чисел Z₁=5-2i    Z₂=1-4i  

7.   Найти 

8.    Найти 

1.     Сложить два комплексных числа  Z₁=2+5i  Z₂=4-3i

2.     Сложить два комплексных числа  Z₁=-4+10i    Z₂=5+3i  

3.     Найти разность комплексных чисел Z₁=10-25i  Z₂=1-3i

4.     Найти разность комплексных чисел  Z₁=-5+10i    Z₂=1+3i

5.     Найти произведение комплексных чисел   Z₁=1-i    Z₂=3+6i

6.     Найти произведение комплексных чисел Z₁=5-2i    Z₂=1-4i  

7.   Найти 

8.    Найти