конспект урока "Исследование функции на монотонность"

Учитель: Кузнецова Н.В.

Предмет: Алгебра и начала математического анализа.

Класс: 10

УМК: Алгебра и начала математического анализа. 10-11 классы А.Г. Мордкович,  2019г.

Уровень обучения: базовый уровень

Тема: Исследование функции на монотонность

Общее количество часов, отведенное на изучение темы: 2

Место урока в системе уроков по теме: 1

Цель: выявить связь между характером монотонности функции и знаком её производной

Задачи:

Обучающие:

дать представление о связи свойств функции с её производной, учить чтению и анализу графиков функций;

развивать умение анализировать, сопоставлять, сравнивать, формулировать выводы по результатам собственной деятельности.

            Развивающие:

развивать такие качества личности, как ясность и точность мысли, логическое мышление, алгоритмическая культура, интуиция, критичность.

           Воспитательные:

воспитывать средствами математики культуру личности: умения выслушать и принимать во внимание взгляды других людей, умение справляться с неопределённостью и сложностью.

Планируемые результаты:

знать связь между характером монотонности функции и знаком её производной;

уметь  исследовать интервалы монотонности функции.

Техническое обеспечение урока: компьютер, проектор,  презентация, учебник. 

Дополнительное методическое и дидактическое обеспечение урока: слайды презентации, карточки с заданиями.

Содержание урока:

1.     Организационный момент.

2.     Актуализация знаний.

3.     Постановка проблемы. Формулировка темы урока, цели. Объяснение нового материала.

4.     Первичное усвоение новых знаний.

5.     Первичная проверка понимания.

6.     Первичное закрепление.

7.     Информация о домашнем задании, инструктаж по его выполнению

8.     Рефлексия (подведение итогов занятия)

Ход урока

I. Организационный момент.

    II.   Актуализация знаний.

 1. Проверка д/задания - № 29.14 (а) – один ученик у доски

 2. Класс: Игра – соревнование «Найди себе пару» (Слайд 2)

Задание:  Выписать пары (номера)  «функция» - «производная».

На столах учащихся раздаточный материал в виде таблицы.

    Взаимопроверка по слайду

Ответы:    1-9,   2-4,   3-5,  4-19,  5-19,  6-10,  7-18,   8-17,  10-20,  11-2,  12-19,    15-16,   16-19   17-13.   (слайд 3)

Проверка домашнего задания:

№ 29.14 (а). Составить уравнение касательной к графику функции y=f(x) в точке с абсциссой x = a, если: F(x) = 2, а = 2.

                                                                                                         Ответ: y = 3x - 4

Дополнительные вопросы: 1. Назови угловой коэффициент касательной (3)

 2. График касательной к функции в точке а = 2 возрастает или убывает? Почему?

3. Возрастает или убывает график функции F(x) = 2.

4. В чём заключается геометрический смысл производной?

III. Постановка проблемы. Формулировка темы урока, цели. Объяснение нового материала.

Вспомним что такое монотонность функции. Обратимся к геометрическому смыслу производной.

1.      –укажите количество промежутков монотонности функции (слайд 4)

-  как ведёт себя касательная в каждой точке промежутка,

- какой знак будет иметь угловой коэффициент касательной,

- как найти угловой коэффициент касательной?

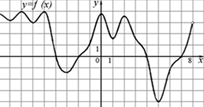
2. На рисунке изображен график функции  у = f(x). (Слайд 5)

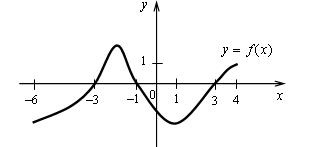
а) Какой знак имеет производная этой функции в следующих точках: –5; –3; –2; 0; 1; 3?

б) Назовите ещё несколько точек, в которых производная больше нуля; меньше нуля.

в) Какой знак имеет производная функции  у = f(x) на промежутке (–6; –2); (–2; 1); (1; 4)?

г) Сделайте предположение о связи между характером монотонности функции и знаком её производной.

·        Чем мы с вами будем заниматься дальше на уроке? (Исследовать функцию на монотонность)

·        Сформулируйте тему урока. (Исследование функции на монотонность)

·        Какую цель поставим для себя в результате данного исследования? (выявить связь между характером монотонности функции и знаком её производной)

Слайд 6. Тема урока «Исследование функции на монотонность»

IV. Первичное усвоение новых знаний.

Работа с учебником: (слайд 7)

Страница учебника 204 – 207 ( эл. учебник:178 – 181)

Прочитать, выписать ответы на вопросы:

·        Какая связь между характером монотонности функции и знаком её производной;

·        теорема о возрастании функции;

·        теорема об убывании функции;

·        теорема о постоянстве функции;

·        разобрать пример 2 (а)

V. Первичная проверка понимания. (слайды 8 – 9)

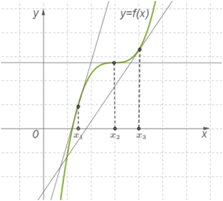
Теорема 1. Если во всех точках открытого промежутка X выполняется неравенство f′(x)≥0 (причем равенство f′(x)=0 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке) , то функция y=f(x)) возрастает на промежутке X.

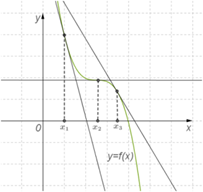
Теорема 2. Если во всех точках открытого промежутка X выполняется неравенство f′(x)≤0 (причем равенство f′(x)=0 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция y=f(x) убывает на промежутке X.

Итак: если существует производная функции в интервале (a,b) и в данном интервале

1) f'(x)>0, то функция в нём возрастает;

2) f'(x)<0, то функция в нём убывает

3) f'(x)=0, то функция постоянна

VI. Первичное закрепление.

·        Как исследовать функцию на монотонность?

·        Сформулируйте алгоритм

·        Определите промежутки монотонности функции

y = 2 – 3- 36х + 40

VII. Информация о домашнем задании, инструктаж по его выполнению.

Дома: п 30 (1)  № 30.12 (а), № 30.14 (а)

VIII. Рефлексия (подведение итогов занятия)

– Если функция  у = f(x) возрастает на некотором промежутке, то что можно сказать о знаке её производной на этом промежутке?

– Если производная некоторой функции  у = f(x) принимает на промежутке только отрицательные значения, то что можно сказать о характере монотонности этой функции на этом промежутке?

– Сформулируйте теоремы, устанавливающие связь между характером монотонности функции и знаком её производной.