Логарифмическая функция, её свойства и график

урок математики 1 курс, спо

Технологическая карта (план) занятия № 22

							Группа	Дата
Дисциплина			Математика, 1 курс
Тема занятия			Логарифмическая функция, её свойства и график

Вид занятия			Теоретическое
Тип занятия			урок изучения и первичного закрепления нового материала
Цель занятия			Познакомить учащихся с понятием логарифмической функции её свойствами и графиком.
Задачи занятия			*Образовательная: направить студентов на самостоятельное определение понятия «логарифмическая функция», сформировать умение строить график логарифмической функции, изучить основные свойства функции, Развивающая:* развить исследовательские умения, выработать умение выделять проблему, сравнивать, сопоставлять, анализировать и обобщать полученные результаты, формировать графическую и функциональную культуру. *Воспитательная*: воспитывать информационную культуру, выработать навыки работы в группе и индивидуально.
Результат		Должны знать				· определение логарифмической функции, свойства логарифмической функции, вид графика в зависимости от основания логарифмической функции; · связь между логарифмической и показательной функцией.
		Должны уметь				применять определение логарифмической функции, свойства логарифмической функции при решении практических заданий; выполнять задания на чтение графика логарифмической функции.
Показатели оценки результата						· определяют свойства логарифмической функции по ее графику; · научились строить график логарифической функции и исследовать их.
Межпредметные связи					Физика, механика, электроника.
	Средства обучения			ПК, проектор, инструкционные карты.
	Основная литература			8. Мордкович А. Г. Алгебра и начало математического анализа. 10 – 11 классы. В 2 ч. Ч.2. Задачник для учащихся общеобразовательных учреждений (базовый уровень). – М., 2015

содержание занятия

№ этапа	Этапы занятия, учебные вопросы, формы и методы обучения		Временная регламентация этапа
1	Организационный этап:		3
	- проверка готовности студентов к занятию;
	- проверка посещаемости;
	- сообщение темы.

2	Мотивационный момент:		2
	- обоснование необходимости изучения данной темы
	для эффективного освоения дисциплин и модулей;
	- вовлечение студентов в процесс постановки целей и задач занятия

3	Актуализация опорных знаний:		10
3.1	Проверка домашнего задания (Разбор нерешенных примеров).
3.2	Вопросы для закрепления теоретического материала к практическому занятию
3.3	Тест по теме «Функции. Область определения и область значения»

4	Изучение нового материала		20
4.1	Исследовательская работа

5	Физминутка		45
6	Закрепление
6.1	Работа у доски
6.2	Работа с учебником
6.3	Тест «Логарифмическая функция»

7	Подведение итогов занятия:		5
	- обсуждение и оценка результатов самостоятельной работы рефлексия
	- выставление оценок.

8	Домашнее задание:		5
	- повторение материала
	Л. 8 № 39.29


Преподаватель
		(И.О. Фамилия)

Конспект занятия № 22

Тема: Логарифмическая функция, её свойства и график

1. Оргмомент.

Девиз урока: (слайд 1)

Омар Хайам: «Расскажи мне, и я забуду,

Покажи мне, и я запомню,

Дай мне сделать самому, и я пойму»

2. Актуализация опорных знаний

- Дома вам было задано повторить основные понятия по теме функция и логарифмы.

- Я вам предлагаю поиграть в игру «Кот в мешке». Правила игры следующие.

Первый вопрос задаю я, тот кто на него отвечает, тот выбирает того кто отвечает на следующий вопрос.

1. Что такое функция? (Функция – это зависимость переменной у от переменной х, при которой каждому допустимому значению х соответствует единственное у)

2. Что такое область определения функции? (Область определения – множество всех допустимых значений аргумента (х – смотрим по оси Ох)

3. Что такое область значения функции? (Область значений – множество всех возможных значений функции (у) - смотрим по оси Оу)

4. Перечислите способы задания функций. (Аналитический, с помощью формулы; табличный; графический)

5. Что такое логарифм? (Логарифм числа b по основанию а это показатель степени, в которую нужно возвести число а, чтобы получить число b причем a > 0, a ≠ 1, b > 0)

- Молодцы.

- Переходим к следующему виду работы. Тест у вас на столе на выполнение 3 мин.

Тест по теме «Функции. Область определения и область значений»

Ответы: в1 – 12122; в2 – 14322

Критерии оценки:

«3» - 3 балла

«4» - 4 балла

«5» - 5 балла

- Время вышло. Ручки положили. Взяли в руки карандаши и обменялись листочками. Ответы и критерии на экране. У вас 30 секунд.

- Кто получил оценку 5, 4, 3.

- За работу по карточкам ….

- Мы с вами повторили основные понятия по теме функция и по теме логарифмы.

- Кто сможет сформулировать тему урока? (может изучать логарифмическую функцию)

- Молодцы. Тема сегодняшнего урока «Логарифмическая функция, ее свойства и график»

- Какую цель мы поставим на уроке? (Познакомимся с понятием логарифмической функции, её свойствами и графиком)

- Открываем тетради, записываем число и тему урока.

3. Изучение нового материала.

1. Исследовательская работа

-Какую функцию вы изучали недавно? (показательную)

- Что вы о ней знаете? (Функция вида у=а^х, где а>0 и а≠1, называют показательной функцией)

-Логарифмическая функция является обратной по отношению к показательной функции. И она имеет следующий вид:

, где а - число, а>0, а1

-Что вы знаете про взаимно обратные функции? (Они симметричны относительно прямой y=x)

- И ещё? (область определения данной функции является областью значений обратной)

-Что это значит? (если график данной функции имеет точку с координатами (х;у), то график обратной ей (у;х))

- Домашним заданием у вас было построить графики функции у= 2^х

- Логарифмическая и показательная функция – это, какие функции? (взаимно обратные)

-Как строятся графики взаимно обратных функций? (симметрично относительно прямой y=x)

Задание №1. Построить график функции в этой же системе координат: у=

Рассмотрим график функции у= и аналогично постройте в этой же системе координат

-Проверяем.

-И так, что по цели урока мы ещё должны сегодня сделать? (Описать свойства логарифмической функции)

- По какому алгоритму мы это делаем? (слайд)

- Опишите в парах свойства первой функции у=

- Проверяем.

- ФИ, какими свойствами обладает функция у= ?

- Поставьте себе «+», у кого задание выполнено верно.

свойство	0 а 1	а 1.
1. Область определения	R₊
2. Множество значений	R
3. Чётность	Ни четная, ни нечётная
4. Периодичность	непериодическая
5. Нули функции	у = 0 при х = 1
6. Монотонность	убывающая	возрастающая
7. Наибольшее значение	нет
8. Наименьшее значение	нет
9. Промежутки знакопостоянства	у 0 при 0 х1 у 0 при х 1	у 0 при х 1 у 0 при 0 х1

- Продолжите работу и опишите свойства функции

- Проверяем.

- Поставьте себе «+», у кого задание выполнено верно.

- Какие свойства отличаются? Как вы думаете, от чего это зависит? (От основания функции. Студенты проговаривают свойства, зависящие от основания функции).

4.Физминутка.

5. Закрепление.

1. Работа у доски.

-Скажите, как построить логарифмическую функцию не используя показательную? (С помощью таблицы значений).

у= (уч-ся у доски)

х			1	3	9
	-2	-1	0	1	2

- Проверяем.

2. Работа с учебником.

№ 42.3 (а,б)

- Объясните, как при сравнении значений логарифмов, вы будете использовать свойство возрастания (убывания) функции.

Основание больше 1, значит функция возрастает.

7< 23, значит 1ое значение < 2ого значения

№ 42.8 (а,в)

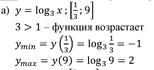
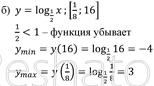
3. Тест «Функции. Область определения и область значений»

1 вариант

2 вариант

Критерии оценки:

1) 2

2) 2; 4

3) 2; 3

4) а) > ; б) <

5) В

1)1

2) 3

3) 1; 3

4) а) <; б) >

5) В; С

«3» - 3 балла

«4» - 4 балла

«5» - 5 балла

6. Домашнее задание

Конспект, Найти дополнительную информацию о логарифмической функции

«3» - № 42.3 (в,г), 42.8 (в,г)

«4» - 42. 10 (а)

«5» - 42.12 (а)

7. Итог урока. Рефлексия

- Какова была цель урока? (Рассмотреть логарифмическую функцию, её график и свойства.)

- Достигли ли вы ее? (да)

- Как вы ее достигли? (Сформулировали определение логарифмической функции, рассмотрели по уже известной схеме все свойства функции, построили её график)

- А также связь между какими функциями вы рассмотрели? (Логарифмическая и показательная функции взаимно обратны)

Логарифмическая функция, её свойства и график

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

27.01.2020