Поурочные разработки по геометрии 7 класс Погорелов

Основные свойства простейших
геометрических фигур (15 часов)

Цель: систематизировать знания учащихся об основных свойствах простейших геометрических фигур.

Урок 1
Геометрические фигуры. Точка и прямая

Цели: ввести понятия геометрии, планиметрии, простейших фигур; систематизировать сведения учащихся о взаимном расположении прямой и точки; заинтересовать в дальнейшем изучении этого предмета.

Ход урока

I. Организационный момент.

Запись темы урока, формулировка цели.

II. Информация о возникновении и развитии геометрии.

Геометрия возникла в результате практической деятельности людей: нужно было строить жилища, прокладывать дороги, устанавливать границы  земельных  паев,  для  этого  необходимо  было  определять  их  размеры. В переводе с греческого слово «геометрия» означает «землемерие» («гео» – по-гречески земля, а «метрео» – мерить). За несколько столетий до нашей эры в Вавилоне, Египте, Китае и Греции уже существовали простейшие геометрические знания, которые добывались в основном практическим путем. Но они не были собраны в единую систему и передавались от поколения к поколению в виде правил, рецептов, не представляя собой научной теории.

Первым, кто начал получать геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес (VI в. до н. э.).

Постепенно геометрия становилась наукой, в которой большинство фактов устанавливалось путем выводов, рассуждений, доказательств. Систематизация знаний начались с V века до н. э. Наибольшее влияние на развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III веке до н. э. Сочинения Евклида «Начала» почти 2000 лет служили основной книгой, по которой изучали геометрию. В этой книге была система геометрических сведений, и геометрия впервые предстала как математическая наука.

В геометрии изучали формы, размеры, взаимное расположение предметов и т. д.

На уроках математики вы познакомились с некоторыми геометрическими фигурами и имеете представление, что такое точка, прямая, отрезок, луч, угол, как они могут быть расположены относительно друг друга. Вы знакомы с понятиями: круг, прямоугольник, квадрат, треугольник. Геометрия дает не только понятия о фигурах, но и знакомит со свойствами, которыми они обладают. Школьный курс геометрии делится на два раздела: планиметрию и стереометрию.

Отрезок, луч, прямая, точка, угол, окружность, треугольник, прямоугольник являются плоскими фигурами, потому что они целиком лежат на плоскости (показать фигуры).

Раздел геометрии, изучающий свойства фигур на плоскости, называется планиметрией.

Учащиеся могут записать основные положения в тетрадь.

III. Изучение нового материала.

1. Запись выводов и определений прямой и точек в тетрадь.

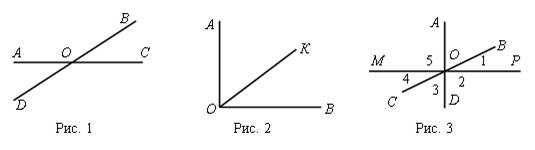
Прямые обозначаются малыми латинскими буквами либо двумя большими буквами, соответствующими двум точкам, лежащим на прямой (сделать рисунок в тетради и записать пояснение).

2. Рассматривание рисунков 3 и 4 по учебнику; ввод символов ; их запись на доске и в тетради.

3. Введем первое свойство: какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.

4. Решение задач.

1) Разобрать задачу 3, решенную в учебнике.

2) Решить задачи 1, 2 на с. 19.

5. Проверочная работа (можно на карточках либо в виде математического диктанта).

1) Начертите прямую, назовите ее любой буквой.

2) Отметьте точку на прямой, дав ей название.

3) Начертите две прямые. Отметьте точку, дав ей название, вне прямой (сделать соответствующие записи).

4) Начертите m, n, пересекающиеся в точке D. Поставьте точки, лежащие и не лежащие на этих прямых (сделать соответствующие записи).

IV. Итог урока.

– Сколько прямых можно провести через две точки?

– Сколько общих точек могут иметь две прямые?

– Как обозначаются точки и прямые?

– Что такое геометрия, планиметрия?

– Что такое точка, прямая?

Задание на дом: пункты 1, 2; ответить на вопросы 1–3; решить задачу 4.

Урок 2
Отрезок. Измерение отрезков

Цели: ввести понятие отрезка; научить измерять отрезки, решать задачи с использованием длины отрезка.

Ход урока

I. Организационный момент.

Сообщение темы урока, формулировка цели.

II. Устная работа.

На рисунке (на доске) изображена прямая, на ней отмечены точки  Назовите все образованные прямые и точки, которые лежат на этих прямых и не лежат на них.

III. Изучение нового материала.

1. Разобрать рисунки 6, 7 по учебнику. Ввести понятие отрезка, концов отрезка, обозначения отрезка.

Отрезком называется часть прямой, которая состоит из всех точек данной прямой, лежащих между этими точками. Эти точки называются концами отрезка.

2. Введем второе свойство: из трех точек на прямой одна и только одна лежит между двумя другими.

3. Введем третье свойство: каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин его частей, на которые он разбивается любой точкой.

4. Для измерения отрезков используются различные измерительные инструменты (линейка с делениями, циркуль и т. д.). (Показать, как измеряются отрезки.)

IV. Решение задач.

1. Разобрать задачу 9, решенную в учебнике, с подробным оформлением (учить оформлять на доске, объясняя, как из условия задачи выделить, что дано и что требуется доказать).

2. Решить на доске и в тетради задачу 7 (1).

Образец решения.

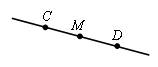
Дано: М Î CD;

  СМ = 2,5 см;

  МD = 3,5 см.

Найти: СD.

Решение:

Чтобы найти длину отрезка СD, надо сложить два составляющих отрезка, то есть СМ + МD = СD, значит, 2,5 + 3,5 = 6 (см).

Ответ: СD = 6 см.

3. Решить задачу 5 с оформлением на доске и в тетради.

V. Самостоятельная работа.

Вариант 1: решить задачи 7(2), 10.

Вариант 2: решить задачи 7(3), 11.

Дополнительное задание: решить задачу 15.

VI. Итог урока.

Задание на дом: пункты 3, 4; вопросы 5, 8; задачи 6, 9, 14.

Урок 3
Отрезок. Измерение отрезков

Цели: ввести понятие отрезка; научить измерять отрезки, решать задачи с использованием длины отрезка.

Ход урока

I. Организационный момент.

Сообщение темы урока, формулировка цели.

II. Устная работа.

– Какие геометрические фигуры вам известны?

Возможные ответы учащихся можно записать на доске, распределив их на две группы:

прямая                                    куб

ломаная                                  цилиндр

отрезок                                  шар

луч                                          конус

прямоугольник                       пирамида

квадрат                                 параллелепипед

многоугольник

– По какому принципу данные геометрические фигуры записаны в двух различных группах? (В первой группе записаны фигуры, существующие на плоскости, а во второй – фигуры, существующие в пространстве.)

1) Начертите прямые а и b, пересекающиеся в точке М. На прямой а отметьте точку Н, отличную от точки М.

а) Являются ли МН и а различными прямыми?

б) Может ли прямая b проходить через точку Н?

III. Решение задач.

1. В треугольнике АВС сторона ВС равна 18 см. Точка М лежит на стороне ВС. Из данных уравнений:

1) 2х + 6 = 18;

2) 2х + 5х = 18;

3) х + 5х = 18;

4) 2х = 5х – выберите такое, которое можно использовать для вычисления длин отрезков ВМ и СМ в следующих случаях:

а) ВМ в 5 раз меньше, чем СМ;

б) ВМ на 5 см меньше, чем СМ;

в) ВМ : СМ = 2 : 5.

2. На отрезке ОР, равном 43 см, взята точка Н. Найдите длину отрезка ОН, если он на 8 см длиннее отрезка РН.

3. Длина отрезка АВ = 6 см, внутри отрезка взята точка М. Найдите длину отрезка ВМ, если:

а) АМ = 2ВМ;

б) 2АМ = 3ВМ;

в) АМ : ВМ = 1 : 5;

г) АМ : ВМ = 3 : 4;

д) АМ – ВМ = 2;

е) 2ВМ + 3АМ = 14.

IV. Итог урока.

Задание на дом:

1. Точки А и В лежат на прямой с. Различны ли прямые АВ и с?

2. Точка С лежит на прямой АВ между А и В. Известно, что отрезок АС на 6 см меньше отрезка ВС. Найдите длины отрезков АС и ВС, если АВ = 24 см.

Точки В, А, С лежат на одной прямой. Может ли точка В разделять точки А и С, если АС = 5 см, а АВ = 7 см?

Урок 4
Полуплоскость. Полупрямая

Цели: ввести понятие полуплоскости, полупрямой; научить различать полупрямые на прямой.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Анализ практической работы.

III. Устная работа.

Решение задач по готовым чертежам.

Дано: АВ = 6 см;                      Дано: МР = 12 см;

 ВС = 9 см.                                КР = 3 см.

Найти: АС.                              Найти: МК

Дано: DO = 9,3 см.              Дано: КС = 9 см, РН = 8 см,

Найдите ошибку.                          КН = 12 см.

                                            Найти: РС.

IV. Самостоятельная работа (3–5 минут).

Карточка 1

Дано: КР – РЕ = 3 см, КЕ = 21 см.

Найти: КР и РЕ.

Карточка 2

Дано: DО = 24 см, ОЕ = 3DО.

Найти: DЕ и ОЕ.

Карточка 3

Дано: АВ = 28 см, АС : СВ = 4 : 3.

Найти: АС и СВ.

Карточка 4

Дано: АВ = ВС, СD = DЕ.

Найти: 1) ВD, если АЕ = 20 см;

            2) АЕ, если ВD = 12 см.

V. Изучение нового материала.

1. Вспомнить, что такое плоскость. По рисунку 9 учебника ввести понятие полуплоскости.

Прямая, лежащая в плоскости, разбивает ее на две полуплоскости.

2. Ввести четвертое основное свойство: прямая разбивает плоскость на две полуплоскости.

3. Ввести определение полупрямой (луча).

Полупрямой или лучом называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной точки.

4. Дать определение начальной точки, ввести определение дополнительных полупрямых.

Данная точка, от которой исходит луч, называется начальной точкой. Различные полупрямые одной и той же прямой, имеющие общую начальную точку, называются дополнительными полупрямыми.

5. Объяснить рисунок 12, зарисовать в тетрадь, сделать соответствующие записи.

VI. Решение задач.

Решить задачи 18, 20, 21.

VII. Итог урока.

– Назовите различие луча и полупрямой.

– Что такое дополнительная полупрямая?

– Что такое начальная точка?

– Что такое полуплоскость и в чем ее отличие от плоскости?

Задание на дом: пункты 5, 6; вопросы 11, 12; разобрать задачи 17, 22; решить задачи 13, 19.

Урок 5
Полуплоскость. Полупрямая

Цели: ввести понятие полуплоскости, полупрямой; научить различать полупрямые, прямые, плоскости и полуплоскости.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Проверка домашней работы. Анализ самостоятельной работы.

III. Устная работа.

Вопросы и задания:

1. На сколько частей разделяют плоскость три прямые, пересекающиеся в одной точке?

2. На сколько частей разделяют плоскость три попарно пересекающиеся прямые?

3. На плоскости отмечены семь точек. Любые из них не лежат на одной прямой. Проведите три прямые так, чтобы в каждой части плоскости оказалось ровно по одной точке. Покажите на рисунке, как это можно сделать.

IV. Решение задач.

Решить задачи 23, 25.

V. Итог урока.

Задание на дом: пункты 5, 6; задачи 24, 37.

Урок 6. Угол

Цели: ввести понятие угла; рассмотреть различные виды углов; научить измерять углы.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Самостоятельная работа (10 минут).

Вариант 1

1. На прямой b отмечены точки С, D, Е так, что CD = 6 см, DЕ = 8 см. Какой может быть длина отрезка СЕ?

2. Точка М – середина отрезка АВ; МВ = 5 дм. Найдите длину отрезка АВ.

Вариант 2

1. На прямой m отмечены точки А, В, С так, что АС = 12 см, АВ = 8 см. Какой может быть длина отрезка ВС?

2. Точка Р – середина отрезка MN. Найдите длину отрезка PN, если MN = 14 дм.

Два ученика работают по карточкам у доски.

Карточка 1

Точка N лежит на прямой MK между точками M и K. Найдите расстояние между серединами отрезков MN и NK, если MN = 7 см, NK = 12 см.

Карточка 2

На отрезке ОР, равном 42 см, взята точка Н. Найдите длину отрезка ОН, если он на 8 см длиннее отрезка РН.

IV. Изучение нового материала.

1. Запись определения. Углом называется фигура, которая состоит из точки – вершины угла – и двух различных полупрямых, исходящих из этой точки, – сторон угла.

2. Вводятся различные способы обозначения угла.

Угол может обозначаться несколькими способами:

ÐО, Ð(ab), ÐFDC.

3. Вводятся понятия углов (развернутый, неразвернутый) по рис. 14, 15 учебника (зарисовать в тетрадь).

Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.

4. Записать определения тупого угла, острого угла, прямого угла и зарисовать.

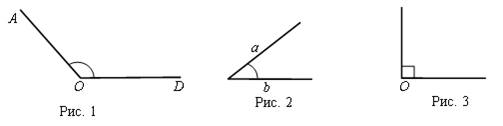
ÐАОД, тупой угол  – это угол, градусная мера которого превышает 90° (рис. 1).

Ð(ab), острый угол – это угол, градусная мера которого меньше 90° (рис. 2).

ÐО, прямой угол – это угол, градусная мера которого равна 90° (рис. 3).

5. Записать в тетрадь основное пятое свойство: каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

V. Решение задач.

Задача 1. Дано: ÐАОВ = 45°, ÐВОС = 21°. 

Найти ÐАОС.

Задача 2. Дано: ÐEDK = 36°.

Найти: ÐFDK.

VI. Итог урока.

-   Что такое угол?

-   Что такое развернутый, неразвернутый угол?

-   Какие еще углы вы знаете?

-   Какими единицами измеряются углы?

-   Сформулировать основное пятое свойство.

-   Из чего состоит угол?

Задание на дом: пункт 7; вопросы 13–19; задача 26.

Урок 7. Угол

Цели: закрепить понятие угла, видов углов; научить измерять углы и применять полученные знания при решении задач.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Анализ самостоятельной работы.

Объявить результаты, провести работу над ошибками.

III. Решение задач.

1.  Луч m проходит между сторонами угла (bc), равного 80°.  Найдите Ð(bm), если он в 3 раза больше, чем Ð(сm).

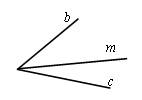
Решение:

Ð(bс) = Ð(bm) + Ð(mс) = 80°. Пусть х° будет равен угол (bm), тогда угол (mc) будет равен 3х, так как сумма равна 80°, то составим и решим уравнение:

х + 3х = 80°

4х = 80°

х = 20.

Ответ: Ð(bm) = 20°.

2. Полупрямая  а  проходит  между  сторонами  угла (bс).  Найдите угол (ас), если угол (bс) равен 97°, угол (bа) = 54°.

3. На отрезке ОР, равном 42 см, взята точка Н. Найдите длину отрезка ОН, если он в 4 раза больше отрезка РН.

IV. Итог урока.

Задание на дом: составить кроссворд, используя изученные термины.

Урок 8
Откладывание отрезков и углов.
Биссектриса угла

Цель: научить строить отрезки и углы.

Ход урока

I. Организационный момент.

Формулировка темы и цели урока.

II. Проверка домашнего задания.

1. Устный опрос по вопросам учебника.

2. Решение дополнительной задачи на доске.

III. Изучение нового материала.

1. Работа по учебнику: чтение пункта 8, запись свойств VI, VII в тетрадь.

Свойство VI. На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.

Свойство VII. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.

Биссектриса угла – луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.

2. Рассмотреть рисунок 41.

IV. Решение задач.

1. Дополнительная задача для устного счета.

Луч ВО является биссектрисой угла АВС. Сделайте рисунок, закончите записи:

а) если ÐАВС = 76°, то  ÐОВА =  

б) если ÐСВО = 44°, то  ÐАВС =  

2. Решить задачи 27, 29 после § 1, задачу 15 после § 2.

V. Итог урока.

Задание на дом: пункты 8, 18; задачи 28, 31 после § 1; задача 16 после § 2.

Урок 9
Решение задач.
Откладывание отрезков и углов

Цель: научить строить отрезки и углы.

Ход урока

I. Организационный момент.

Формулировка темы и цели урока.

II. Блицопрос.

1. Единица измерения углов. (Градус.)

2. Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле. (Градусная мера угла.)

3. 1/180 часть развернутого угла. (Градус.)

4. 1/60 часть минуты. (Секунда.)

5. 1/60 часть градуса. (Минута.)

6. Градусная мера развернутого угла. (180°.)

7. Градусная мера прямого угла. (90°.)

8. Градусная мера неразвернутого угла. (Меньше 180°.)

9. Угол, градусная мера которого меньше 90°. (Острый.)

10. Угол, градусная  мера  которого  больше  90°,  но  меньше  180°. (Тупой.)

III. Решение задач.

1. Угол АОВ равен 122°, угол АОН равен 19°, угол СОВ равен 23°. Найдите угол СОН.

2. Луч ОС проходит между сторонами угла АОВ, равного 120°. Найдите угол АОС, если угол АОС меньше угла СОВ в 2 раза.

3. Может ли луч с проходить между сторонами Ðаb, если Ðаb = 130°, Ðаd = 130°, Ðас = 40°, Ðсd = 90°?

IV. Итог урока.

Задание на дом:

1. На отрезке АВ взята точка С. Известно, что АВ = 5 см, АС = 7 см. Какую длину может иметь отрезок ВС?

2. На отрезке АВ взята точка Р. Расстояние между серединами отрезков АР и РВ равно 20 см. Найдите длину отрезка АВ.

3. Градусная мера неразвернутого угла ас меньше 180°. Луч р является его биссектрисой, делит угол ас на два равных угла, градусные меры которых меньше 90°, то есть на два острых угла. Поэтому угол ар не может быть прямым или тупым.

Урок 10
Треугольник. Существование треугольника,
равного данному

Цели: ввести определение треугольника; вывести свойства равенства треугольника.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Самостоятельная работа (10 минут).

Вариант I (на оценку «3»)

1. Нарисовать острый угол, дать ему название, разделить его лучом, найти градусную меру полученных углов при помощи транспортира, сделать соответствующие записи.

2. Полупрямая d проходит между сторонами угла (bc). Найдите Ð (dc), если Ð (bc) = 97°, Ð (bd) = 54°.

Вариант II (на оценки «4, 5»)

1. Нарисовать тупой угол, дать ему название, разделить его лучом, найти градусную меру полученных углов при помощи транспортира, сделать соответствующие записи.

2. Луч ON проходит между сторонами угла РОК. Найдите угол РОК, если ÐРОN = 100°, а ÐКОN на  меньше, чем ÐРОN.

Вариант III (на оценки «4, 5»)

1. Нарисовать развернутый угол, дать ему название, разделить его лучом, найти градусную меру полученных углов при помощи транспортира, сделать соответствующие записи.

2. Луч m проходит между сторонами угла (bc), равного 80°.  Найдите  Ð(bm), если он в три раза больше, чем Ð(сm).

III. Изучение нового материала.

1. Дать определение треугольника, сделав рисунок в тетрадях и на доске, стороны, вершины, угла треугольника. Записать в тетрадь.

Стороны – AB, BC, CA.

Вершины – A, B.

Углы – ÐA, ÐB, ÐC.

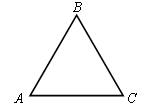
Треугольник – это фигура, которая состоит из трех точек, не лежащих на одной прямой, трех отрезков, попарно соединяющих эти точки.

Два отрезка называются равными, если они имеют одинаковую длину, а углы будут равными, если у них одинаковая градусная мера.

2. Рассмотреть рис. 22, сделать запись о равенстве треугольников в тетрадь. Показать, как обозначаются равные треугольники.

Треугольники называются равными, если у них соответствующие углы и стороны равны.

3. Основное восьмое свойство: каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

IV. Решение задач.

Решить задачи 33, 36.

V. Итог урока.

– Что такое треугольник?

– Какие треугольники называются равными?

– Какие отрезки и углы называются равными?

Задание на дом: пункты 9, 10; задачи 37, 38.

Урок 11
Треугольник. Существование треугольника,
равного данному

Цели: закрепить определение треугольника; рассмотреть свойства равенства треугольника; развивать логическое мышление учащихся.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Анализ самостоятельной работы.

Рассмотреть типичные ошибки, показать правильное решение.

III. Решение задач.

1. Задачи 40, 41.

2. Дополнительная задача.

На прямой отмечены точки А, В, С так, что АВ = 7 см, АС = 21 см, ВС =28 см. Какая из этих точек лежит между двумя другими?

IV. Итог урока.

Задание на дом: задача 39.

Дополнительная задача.

Один из углов, образовавшихся при пересечении двух прямых, равен 21°. Найдите остальные углы.

Урок 12
Параллельные прямые

Цели: ввести определение параллельных прямых; научить различать их на плоскости.

Ход урока

I. Организационный момент.

Сообщение темы урока и постановка цели.

II. Изучение нового материала.

1. Предложить учащимся рассмотреть всевозможные случаи взаимного расположения прямых, используя готовые чертежи; подвести к рассуждению о расположении прямых по рис. 1, сделать выводы.

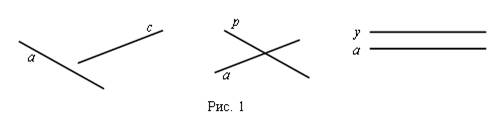
2. Дать определение параллельных прямых.

Две прямые называются параллельными, если они не пересекаются.

3. Ввести обозначение параллельных прямых, сделать рис. 2.

Параллельные прямые обозначаются знаком ||.

Например: a || c, см. рис. 2.

III. Закрепление изученного материала.

Решение задач 4, 1.

IV. Итог урока.

– Какие прямые называются параллельными?

– Начертите три параллельные прямые и сделайте соответствующую запись.

Задание на дом: пункты 11, 29; вопрос 1; задачи 2, 3.

Урок 13
Теоремы и доказательства. Аксиомы

Цель: ввести понятие теоремы и аксиомы.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Изучение нового материала.

1. Разобрать материал в учебнике (пункты 12, 13), записать теорему 1.1, смысл доказательства.

2. Аксиома – утверждение, не требующее доказательства. Все восемь основных свойств называются аксиомами, они не требуют доказательства.

III. Решение задач.

Решить задачу 42.

IV. Итог урока.

– Что такое теорема?

– Что такое аксиома?

– Что такое доказательство теоремы?

– В чем смысл доказательства?

Задание на дом: пункты 12, 13.

Дополнительная задача.

Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 83° больше другого.

Урок 14
Решение задач

Цель: выработать у учащихся умение применять при решении задач изученный материал.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Анализ практической работы.

Объявить результаты, рассмотреть типичные ошибки, показать правильное решение.

III. Решение задач.

1. Три точки В, С, D лежат на одной прямой. Известно, что ВD = 17 см, DC = 25 см. Какой может быть длина отрезка ВС?

2. Сумма вертикальных углов МОЕ и DОС, образованных при пересечении прямых МС и DЕ, равна 204°. Найдите угол МОD.

3. С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла.

4. Лежат ли точки M, N, P на одной прямой, если МР = 5 см, MN = 12 см, РN = 8 см? В каком случае это возможно?

IV. Итог урока.

Задание на дом: повторить изученный материал, подготовиться к контрольной работе.

Решить задачи:

1. Найдите углы, образованные при пересечении двух прямых, если разность двух из них равна 37°.

2. Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108°. Найдите угол ВОD.

Урок 15
Контрольная работа № 1 по теме
«Основные геометрические свойства
простейших фигур»

Цель: проверить знания, умения и навыки учащихся.

Контрольную работу можно провести по вариантам.

Ход урока

I. Организационный момент.

II. Выполнение контрольной работы.

Вариант 1

1. D MNF = D DEF, MN = 13 см, Ð FE = 75°. Найдите длину стороны DE и градусную меру угла N.

2. Точка О лежит между точками Р и Н, причем ОР = 7 см, ОН = 11,3 см. Найдите расстояние между точками Р и Н.

3. Прямой угол АОВ разделен лучом ОС на два угла. Один из них на 12° больше другого. Найдите градусную меру полученных углов.

Вариант 2

1. D BCD = D JST, JS = 18 см, Ð D = 115°. Найдите градусную меру угла Т и длину стороны ВС.

2. Точка С лежит между точками А и В, причем АВ = 15 см, АС = 6,8 см. Найдите расстояние между точками В и С .

3. Прямой угол АОВ разделен лучом ОС на два угла. Один из них в 4 раза больше другого. Найдите градусную меру полученных углов.

III. Задание на дом.

Повторить дома весь изученный материал, подготовиться к зачету по теме «Начальные сведения геометрии», который будет проводиться во внеурочное время.

Зачет состоит из двух вариантов, его лучше провести за два-три урока до окончания темы, чтобы осталось время исправить обнаруженные недочеты. День зачета назначается заранее. Учащийся, выполнивший обязательную часть, получает отметку «зачет», после чего он может получить оценки «4» или «5» за выполнение дополнительной части. Учащийся, не сдавший зачет, обязан его пересдать. Можно внести коррективы по своему усмотрению, в зависимости от уровня подготовленности учащихся.

Дополнительными заданиями к зачету могут быть такие: комментирование учащимися решения задач, пояснение тех свойств, которыми пользовались при решении, формулировка определений фигур и понятий, применяемых в решении, ответы на вопросы после § 1 учебника.

Задания для подготовки к зачету
«Начальные геометрические сведения»

1. На прямой КМ отмечены точки А, В, С (в этом порядке). Выпишите все образовавшиеся: а) отрезки; б) лучи.

2. Запишите угол (рис. 1): а) больший угла АОD; б) меньший угла АОD.

3. На рис. 2 углы 1, 2 и 3 равны. Укажите: а) биссектрису угла АОС; б) угол, биссектрисой которого является луч ОС.

4. Точка С – середина отрезка АВ, равного 28 см, а точка D – середина отрезка ВС. Чему равна длина отрезка АD?

5. Начертите какой-нибудь тупой (острый) угол и с помощью транспортира определите его градусную меру.

6. Луч ОВ делит угол АОС на два угла (рис. 3). Чему равен угол АОС, если ÐВОС = 32°, ÐАОВ = 65°?

7. На рис. 4 ÐАОВ = 112°. Найдите ÐВОD.

8. На рис. 5 ÐАОС = 54°. Найдите ÐВОD.

9. Найдите угол, смежный с углом АВС, если  угол АВС равен: а) 52°; б) 87°.

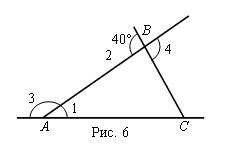
10. Луч ВD – биссектриса угла АВС (рис. 6). Чему равен:

а) ÐАВD, если ÐАВС = 88°?

б) ÐАВС, если ÐАВD = 36°?

11. На рис. 7 прямые АВ и СD перпендикуляры. Выпишите по одному тупому и острому углу со стороной OD.

12. Прямые АО и ВО перпендикулярны (рис. 8). Луч ОК – биссектриса угла АОВ. Найдите ÐАОК.

13. Угол АОВ разделен лучом ОС на два угла, один из которых вдвое больше другого и равен 60°. Какова величина угла АОВ?

 

Зачет № 1 «Начальные геометрические сведения»

Этот вариант проводится в виде письменной работы.

Вариант I

Обязательная часть.

1. Точка С – середина отрезка АВ, равного 18 см, а точка D – середина отрезка АС. Чему равна длина отрезка АD?

2. Найдите величины углов ВОС и DОС, если ÐАОВ = 110° (рис. 1).

3. Луч ОК – биссектриса прямого угла АОВ (рис. 2). Найдите величину угла АОК.

Дополнительная часть.

4. Угол АОВ разделен лучом ОС на два угла, один из которых вдвое больше другого и равен 80°. Чему равен угол АОВ?

5. Найдите величины углов 1, 2, 3, 4 и 5, если прямые АD и СК перпендикулярны, а ÐАОВ = 63° (рис. 3).

Вариант 2

Обязательная часть.

1. Точка С – середина отрезка АВ, равного 16 см, а точка D – середина отрезка СВ. Чему равна длина отрезка DВ?

2. Найдите величину углов ВОС и DОС, если ÐАОВ = 54° (рис. 4).

3. Луч ОК – биссектриса прямого угла АОВ (рис. 5). Найдите величину угла КОВ.

Дополнительная часть.

4. Луч АОВ разделен лучом ОС на два угла, один из которых вдвое меньше другого и равен . Чему равен угол АОВ?

5. Найдите величину углов 1, 2, 3, 4 и 5, если прямые АD и СК перпендикулярны, а ÐАОВ = 42°.

Смежные и вертикальные углы (7 часов)

Цели: ввести понятия смежных и вертикальных углов; научить применять свойства этих углов при решение задач и различать их.

Урок 16
Смежные углы

Цели: дать определение смежных углов; научить применять теорему о смежных углах при решении задач.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Анализ контрольной работы.

III. Проверка домашнего задания.

Во время проверки домашнего задания два ученика решают задачи по карточкам, затем всем классом разбирают правильность решения и оценивают ответы одноклассников.

Карточка 1

Известно, что D МРК = D CDE. Запишите все равные стороны и углы этих треугольников.

Карточка 2

Дано: D МВЕ = D КОР, DE = 4,5 см, DB = 9 см, ÐD = 60°, ÐВ = 30°.

Найти соответствующие стороны и углы треугольника. Чему они равны?

IV. Изучение нового материала.

1. На доске нарисованы смежные углы, по ним дается определение:

Два угла называются смежными, если у них одна общая сторона, а другие стороны являются дополнительными полупрямыми.

2. Сформулировать теорему о смежных углах.

Сумма смежных углов равна 180°.

Вынести доказательство на доску.

3. Записать следствия из данной теоремы.

Если два угла равны, то смежные с ними углы равны.

Если угол не развернутый, то его градусная мера меньше 180°.

Угол, смежный с прямым углом, есть прямой угол.

V. Решение задач.

1. Решение задач по готовым чертежам.

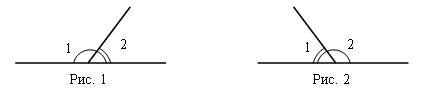
Дано: Ð1 – Ð 2 = 30°.                        Дано: Ð1 = Ð2 – 90°.

Найдите: Ð1, Ð2.                               Найдите: Ð1, Ð2.

Решение: Выразим угол 1 через угол 2, получим Ð1 = 30 ° + Ð2. Так как сумма смежных углов равна 180°, то получим уравнение, где Ð2 примем за новую переменную х. Решим полученное уравнение: 30° + х + х = 180° 2х = 150° х = 75° Ð2 = 75°, значит,  Ð1 = 30° + 75° = = 105°. Ответ: Ð1 = 105°, Ð2 = 75°.

Вторая задача решается аналогично. Ответ:  Ð1 = 45°,    Ð2 = 135°.

2. Решение задач 3, 4, 5 по учебнику.

VI. Итог урока.

Задание на дом: пункты 14; вопросы 1, 4, 5; задачи 1, 2, 6.

Дополнительная задача.

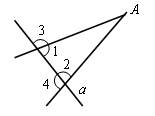
Прямая а пересекает стороны угла А. Докажите, что Ð1 = Ð2, если известно, что Ð3 = Ð4.

Урок 17
Смежные углы

Цели: закрепить полученные знания о смежных углах; научить применять теорему о смежных углах при решении задач.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Проверка домашней работы.

III. Решение задач.

1) Смежные углы относятся как 1 : 2 . Найдите эти смежные углы.

2) Один из смежных углов больше другого на 20°. Найдите эти углы.

3) Один из углов, образовавшихся при пересечении двух прямых, равен 21°. Найдите остальные углы.

4) Меньший из смежных углов в 4 раза меньше разности этих смежных углов. Найдите эти смежные углы.

5) Докажите, что сумма каждых трех углов, не прилежащих один к другому и образуемых тремя прямыми, проходящими через одну точку, равна двум прямым углам.

IV. Итог урока.

– Могут ли два смежных угла быть оба:

1) острыми;

2) тупыми;

3) прямыми?

– Какой вывод можно сделать из этого?

Задание на дом: пункт 14.

Дополнительные задачи.

1. Один из смежных углов составляет 0,2 другого. Найдите эти смежные углы.

2. Один из четырех углов, образовавшихся при пересечении двух прямых, в 11 раз меньше суммы трех остальных углов. Найдите эти четыре угла.

Урок 18
Вертикальные углы

Цели: ввести понятие вертикальных углов; доказать теорему о вертикальных углах; научить применять знания о вертикальных углах при решении задач.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Устная работа.

Задача 1.

Один из углов, полученный при пересечении двух прямых, равен 118°. Найдите остальные три угла.

Задача 2.

Дополните рисунок, чтобы образовалось четыре смежных угла.

III. Изучение нового материала.

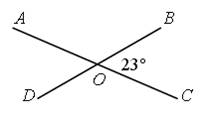
1. Вспомнить, что такое дополнительные прямые, после чего дать определение вертикального угла.

2. Записать теорему: Вертикальные углы равны. Доказательство разбирается всем классом, оформляется на доске и записывается учащимися в тетрадь.

IV. Решение задач.

1. Коллективный разбор задачи.

Найти: ÐАОВ, ÐАОD, ÐCОВ.

2. Решение задач 7, 9 по учебнику.

V. Итог урока.

– Что такое вертикальные углы?

– Какими свойствами они обладают?

– В чем различие между вертикальными и смежными углами?

Задание на дом: пункты 15; задачи 8, 10, 12.

Урок 19
Перпендикулярные прямые.
Доказательство от противного

Цели: ввести понятие перпендикулярной прямой, перпендикуляра; познакомить с методом доказательства от противного.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Проверка домашнего задания.

Один ученик решает задачу 11, затем проводится коллективное обсуждение решения этой задачи.

III. Изучение нового материала.

1. Ввести понятия перпендикуляра, перпендикулярной прямой, основания перпендикуляра, обозначения перпендикуляра.

Две прямые называются перпендикулярными, если они пересекаются под прямым углом.

На рисунке а^с.

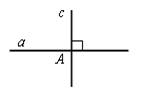
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец называется основанием перпендикуляра.

2. Прочитать пункт 17, сделать выводы и записать их в тетрадь.

Доказательство от противного состоит в том, что нужно сделать предположение, противоположное тому, которое утверждается в теореме. Затем путем рассуждений, опираясь на аксиомы и ранее доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо какой-то аксиоме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.

3. Доказать теорему о перпендикулярных прямых.

Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.

Для доказательства использовать метод от противного.

4. Показать, как строить перпендикулярные прямые.

IV. Решение задач.

1. Дополнительная задача.

Даны ÐАОЕ – развернутый, ÐАОВ на 40° меньше, чем ÐDOE, ÐВОС на 40° больше, чем ÐDOС. Доказать, что  СО || АЕ.

2. Решить задачи 13, 14.

V. Практическая работа.

Необходимо построить произвольный треугольник, отметить на каждой стороне точку, назвать ее и провести перпендикуляры через эти точки к сторонам треугольника.

VI. Итог урока.

– Что такое перпендикулярные прямые?

– Что называется перпендикуляром?

– Что такое основание перпендикуляра?

– В чем заключается смысл доказательства от противного?

Задание на дом: пункты 16, 17, 19; задачи 23, 24.

Урок 20
Решение задач

Цель: выработать у учащихся умение применять полученные знания при решении задач.

Ход урока

I.Организационный момент.

Формулировка темы и постановка цели урока.

II. Анализ практической работы.

Объявить результаты, выявить ошибки, сделать работу над ошибками.

III. Решение задач.

1. Три точки В, С, D лежат на одной прямой. Известно, что ВD = 17 см, DС = 25 см. Какой может быть длина отрезка ВС?

2. Сумма вертикальных углов МОЕ и DОС, образованных при пересечении прямых МС и DЕ, равна 204°. Найдите угол МОD.

3. С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла.

4. Лежат ли точки M, N, P на одной прямой, если МР = 5 см, MN = 12 см, PN = 8 см. В каком случае это возможно?

5. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 83° больше другого.

IV. Итог урока.

Задание на дом: решить задачи.

1) Сумма углов равна 178°. Докажите, что эти углы не могут быть смежными.

2) Разность смежных углов равна 54°. Определите величину другого угла.

Урок 21
Решение задач

Цели: повторить, систематизировать и обобщить знания по теме.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Решение задач.

1. Сумма трех углов, образованных при пересечении двух прямых, на 280° больше четвертого угла. Найдите эти углы.

2. Сумма вертикальных углов в 5 раз меньше угла, смежного с каждым из них. Найдите эти вертикальные углы.

3. Какое наименьшее число лучей можно провести из одной точки, чтобы все углы, ограниченные соседними лучами, были острыми?

4. Точки А, В и С лежат на одной прямой, причем длина отрезка ВС больше длины отрезка АС в 3 раза, а длина отрезка АВ меньше длины ВС на 3,6 см. Найдите длину отрезка АС.

Задание на дом: повторить изученный материал, подготовиться к контрольной работе. Решить задачи:

1) Найдите неразвернутые углы, образованные при пересечении двух прямых, если разность двух из них равна .

2) Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108°. Найдите угол ВОD.

Урок 22
Контрольная работа № 2 по теме
«Смежные и вертикальные углы»

Цель: проверить знания, умения и навыки учащихся.

Контрольную работу можно провести по вариантам.

Ход урока

I. Организационный момент.

II. Выполнение работы.

Вариант 1

1. Прямые АВ и СD пересекаются в точке О.

а) Выпишите две пары смежных углов. Каким свойством они обладают?

б) Какие из углов, образовавшихся при пересечении этих прямых, равны? Как они называются?

2. а) Один из смежных углов в 3 раза меньше другого. Найдите эти углы.

б) Могут ли два смежных угла быть тупыми? Ответ обоснуйте.

Вариант 2

1. Прямые РН и ОМ пересекаются в точке Х.

а) Выпишите две пары смежных углов. Каким свойством они обладают?

б) Какие из углов, образовавшихся при пересечении этих прямых, равны? Как они называются?

2. а) Один из смежных углов на 50° меньше другого. Найдите эти углы.

б) Может ли один из вертикальных углов быть тупым? Ответ обоснуйте.

III. Итог урока.

Задание на дом: повторить § 1, 2; вопросы на с. 15–16, 26.

Можно провести контрольную работу с использованием дифференцированных заданий.

Задания на оценку «3»

Карточка 1

1. Известно, что DАВС = DKHP. Запишите равные углы и стороны в данных треугольниках.

2. Сформулируйте основные свойства принадлежности точек и прямых  на плоскости.

3. По рисунку выполните задания.

а) Среди углов, полученных при пересечении прямых АD и ВС, найдите и запишите углы, смежные с ÐАОС.

б) Дайте определение смежных углов.

4. а) Постройте отрезок АВ = 3 см.

б) На отрезке АВ отметьте точку С так, чтобы АС = 3 см.

в) Найдите длину отрезка ВС.

Карточка 2

1. По рисунку ответьте на вопросы.

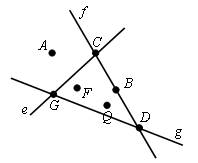
а) Через какие точки проходит прямая g?

б) Какие точки лежат на прямой f?

в) Каким прямым принадлежит точка Q?

2. а) Назовите все углы, изображенные на рисунке.

б) Назовите луч, проходящий между сторонами угла АВD.

в) Чему равна градусная мера угла ABD?

3. Проведите полупрямую АВ. Отложите от этой полупрямой угол ВАС, равный 70°, причем точки С и D лежат в одной полуплоскости. Определите взаимное расположение полупрямых АС и АВ.

4. Прямые ВD и АС пересекаются в точке О. Найдите градусную меру угла СОD, если ÐАОД = 138°.

Задания на оценку «4»

Карточка 1

1. Сформулируйте основное свойство принадлежности точек и прямой на плоскости.

2. Сформулируйте определение равных треугольников.

3. Сформулируйте и докажите теорему о вертикальных углах.

4. Разность смежных углов равна 40°. Определите величину большего угла.

5. Точка С лежит на прямой АВ между А и В. Известно, что отрезок АС на 6 см меньше отрезка ВС. Найдите длину отрезков АС и ВС, если АВ = 24 см.

Карточка 2

1. Сформулируйте и докажите теорему о смежных углах.

2. Сформулируйте основное свойство существования треугольника, равного данному.

3. Сформулируйте основное свойство расположения точек на прямой.

4. На отрезке АС, длина которого равна 24 см, отмечена точка В. Найдите расстояние между серединами отрезков АВ и ВС.

5. Прямые АВ и СD перпендикулярны и пересекаются в точке О. Найдите угол между биссектрисой ÐАОС и полупрямой, дополнительной к ОС.

Карточка 3

1. Сформулируйте основное свойство измерения углов.

2. Сформулируйте основное свойство откладывания углов.

3. Докажите, что если два угла равны, то смежные с ними углы равны.

4. Градусные меры двух углов относятся как 2 : 3. Могут ли эти углы быть вертикальными?

5. От данной полупрямой отложены ÐАВС = 56° и ÐABD = 43°. Найдите ÐDCB.

Карточка 4

1. Сформулируйте основное свойство измерения углов.

2. Докажите, что если два смежных угла равны, то вертикальные им углы равны.

3. Какими свойствами обладает разбиение плоскости на две полуплоскости?

4. Градусные меры двух углов, которые получаются при пересечении двух прямых, относятся как 11 : 9. Найдите эти углы.

5. Луч c проходит между сторонами угла (аb), равного 120°. Чему равны углы (ас) и (bс), если угол (ас) в три раза больше угла (bс)?

Задания на оценку «5»

Карточка 1

1. Точки А и В принадлежат прямой с. Различны ли прямые АВ и с?

2. Верно ли утверждение: На полупрямой от данной точки можно отложить только один отрезок, равный данному? Объясните ответ.

3. Сумма двух углов равна 178°. Докажите, что эти углы не могут быть смежными.

4. Длина отрезка АВ равна 5 см. На отрезке отмечены точки М и Р так, что АМ = 3,1 см и РВ = 2,6 см. Найдите длину отрезка МР.

5. Может ли луч с проходить между сторонами угла (аb), если Ð(ас) = 27°, Ð(сd) = 73°, Ð(аb) = 70°?

Карточка 2

1. Ответьте на вопросы и выполните задания:

а) На сколько частей разделят плоскость три прямые, пересекающиеся в одной точке?

б) На сколько частей  разделят плоскость три попарно пересекающиеся прямые?

в) На плоскости отмечены семь точек. Любые четыре из них не лежат на одной прямой. Проведите три прямые так, чтобы в каждой части плоскости оказалось ровно по одной точке. Покажите на рисунке, как это можно сделать.

2. Верно ли утверждение: На одной полупрямой от ее начала можно отложить только один угол, равный данному? Ответ объясните.

3. Докажите, что биссектрисы углов, образовавшихся при пересечении двух прямых, перпендикулярны или образуют развернутый угол.

4. Разность двух углов равна 178°. Докажите, что эти углы могут быть вертикальными.

5. Длина отрезка АВ равна 1,5 см, на луче АВ отмечена точка М так, что АМ = 0,7 см, а на луче ВА отмечена точка Р так, что ВР = 2,1 см. Найдите длину отрезка МР.

Признаки равенства треугольников (15 часов)

Цель: формировать умение доказывать равенство треугольников с опорой на признаки равенства треугольников.

Урок 23
Первый признак равенства треугольников. Использование аксиом при доказательстве теорем

Цели: сформулировать и доказать первый признак равенства треугольников, научить применять эту теорему при решении задач; развивать логическое мышление.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Анализ контрольной работы.

III. Актуализация знаний.

1. Вспомнить определение смежных и вертикальных углов, их свойства.

2. Вспомнить определения равенства фигур, биссектрисы угла.

3. Вспомнить виды углов.

4. Повторить определения треугольника, его элементов, периметра треугольника, равных треугольников.

5. Повторить VI, VII, VIII аксиомы.

IV. Изучение нового материала.

1. Формулировка первого признака равенства треугольников: если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2. Объяснение доказательства и его запись на доске.

3. Чтение пункта 21 учебника; запись основных выводов в тетрадь.

Учитель показывает учащимся, как можно доказывать теоремы, используя аксиомы.

При доказательстве теорем необходимо указывать, на какую аксиому или теорему делается ссылка.

V. Закрепление изученного материала.

1. Решение задач по готовым чертежам.

1) Найти пары равных треугольников и доказать их равенство (см. рис. 1–4).

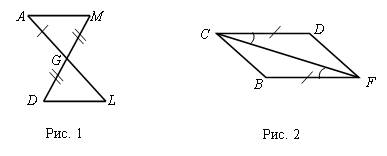
2) Разобрать задачу 1, решенную в учебнике.

2. Решение задачи с подробным оформлением.

Периметр треугольника равен 48 см, а одна из сторон – 18 см. Найдите две другие стороны, если их разность равна 4,6 см.

Дано: Р_DАВС = 48 см, АС = 18 см, ВС – АВ = 4,6 см.

Найти: АВ и ВС.

Решение:

Обозначим длину стороны АВ буквой  см, тогда ВС = (х + 4,6) см. Так как Р_DАВС = АВ + АС + ВС, получаем уравнение:

(х + х + 4,6 + 18) = 48

2х + 22,6 = 48

2х = 25,4

х = 12,7 см

АВ = 12,7 см, ВС = (12,7 + 4,6) = 17,3 см.

Ответ: 12,7 см и 17,3 см.

3. Решение задачи 4 по учебнику.

V. Итог урока.

– В чем заключается смысл равенства треугольника по первому признаку?

Задание на дом: пункты 20, 21; задачи 2, 3.

Дополнительная задача.

Отрезки МК и PR равны. Докажите равенство треугольников SPM и SKR, если известно, что MS = SR. Необходимо сделать рисунок.

Урок 24
Второй признак равенства треугольников

Цели: изучить второй признак равенства треугольников; выработать навыки использования первого и второго признаков равенства треугольников при решении задач; развивать логическое мышление.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Устная работа.

Один ученик доказывает теорему (первый признак равенства треугольника) на доске, остальные учащиеся решают задачи по готовым чертежам.

1) Какие треугольники на рис. 1 равны и почему?

2) На рис. 2 в треугольниках ABD и ACD ÐBAD = ÐCAD, АВ = АС. Найдите периметр DАBD, если АС = 5 см, CD = 3 см, AD больше АС на 2 см.

III. Изучение нового материала.

Формулировка и доказательство второго признака равенства треугольников (на доске и в тетрадях): если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, такие треугольники равны.

При доказательстве признака желательно отметить аналогию с доказательством первого признака.

IV. Закрепление изученного материала.

1. Решение задач по готовым чертежам.

– Докажите, равны ли треугольники.

2. Решение задач 5, 6 по учебнику.

V. Итог урока.

– Что такое смежные углы, вертикальные углы?

– Какое отношение они имеют к первому и второму признакам?

– Сформулируйте первый и второй признак равенства треугольников.

Задание на дом: пункт 23; задача 8.

Дополнительная задача.

Равные отрезки ВЕ и CD пересекаются в точке О. Известно, что ВО = DO, ÐВСО = 40°, ÐВОС = 48°, ÐСВО = 92°. Найдите углы треугольника DEO.

Урок 25
Второй признак равенства треугольников.
Решение задач

Цели: изучить второй признак равенства треугольников; выработать навыки использования первого и второго признаков равенства треугольников при решении задач; развивать логическое мышление.

Ход урока

I. Организационный момент.

Формулировка темы и цели урока.

II. Проверка домашней дополнительной задачи.

III. Самостоятельная работа (15 минут).

Вариант 1

Докажите равенство треугольников ADC и АВС с общей стороной АС, если AD = AB и ÐDAC = ÐВАС. Найдите углы ADC и ACD, если ÐАВC = 108°, ÐАСВ = 32°.

Вариант 2

Докажите равенство треугольников АВС и ADC с общей стороной АС, если AВ = DC и ÐВАС = ÐDCA. Найдите углы АСВ и ADC, если ÐАВC = 102°, ÐВСА = 38°.

Вариант 3 (для более подготовленных учащихся)

Известно, что DАВС = DА1В1С1, причем ÐА = ÐА1, ÐВ = ÐВ1. На сторонах АС и А1С1 отмечены точки D и D1 так, что CD = C1D1. Докажите, что DCBD = DC1B1D1.

IV. Решение задач.

1. Решите задачу с подробным оформлением на доске и в тетради.

Дано: ÐDAB = ÐСВА, ÐСАВ = ÐDBA, АС = 13 см.

Найдите BD.

2. Докажите, что в равных треугольниках биссектрисы, проведенные к соответственно равным сторонам, равны.

V. Итог урока.

– В чем заключается смысл второго признака равенства треугольников?

Задание на дом: пункт 23; задача 7.

Дополнительная задача.

Отрезки  АВ  и  СD  пересекаются  в середине  О  отрезка  АВ, ÐОAD = ÐОВС.

а) Докажите, что DСВО = DDАО.

б) Найдите ВС и СО, если СD = 26 см, АD = 15 см.

Урок 26
Равнобедренный треугольник

Цели: ввести понятия равнобедренного треугольника, равностороннего треугольника; познакомить со свойством углов при основании.

Ход урока

I. Организационный момент.

Сообщение темы урока, формулировка цели.

II. Анализ самостоятельной работы.

III. Изучение нового материала.

1. Дать определение равнобедренного треугольника, после чего ввести понятие равностороннего (объяснять на чертеже).

Треугольник называется равнобедренным, если у него две стороны равны.

В равнобедренном треугольнике две равные стороны называются боковыми.

Третья сторона в равнобедренном треугольнике называется основанием. На рисунке АС – основание, АВ и ВС – боковые стороны.

Треугольник называется равносторонним, если у него все стороны равны.

2. Доказать свойство углов при основании равнобедренного треугольника.

В равнобедренном треугольнике углы при основании равны.

IV. Решение задач.

1. Решение задач по чертежам; повторение изученного ранее материала.

Найти угол DBA.

2. Решить задачу.

Дано: DАВС – равнобедренный.

DВСD – равносторонний.

РDАВС = 40 см; РDВСD = 45 см.

Найти: AB и BC.

3. Решить задачу 10.

V. Итог урока.

– В чем заключается смысл равенства треугольников по второму признаку?

– Чем отличается первый признак равенства треугольников от второго?

– Что такое равнобедренный треугольник?

– Какими свойствами обладает равнобедренный треугольник?

– Какой треугольник называется равносторонним?

– Что такое боковая сторона и основание треугольника?

Задание на дом: пункт 23; вопросы 3, 5, 6; задачи 9, 11, 12.

Урок 27
Равнобедренный треугольник.
Решение задач

Цели: закрепить изученный материал; научить применять свойства равнобедренного треугольника при решении задач.

Ход урока

I. Организационный момент.

Сообщение темы урока, формулировка цели.

II. Решение задач.

1. Дополнительные задачи.

1) Докажите, что если сторона одного равностороннего треугольника равна стороне другого равностороннего треугольника, то треугольники равны.

2) Докажите, что равнобедренные треугольники равны, если основание и прилежащий к нему угол одного треугольника соответственно равны основанию и прилежащему к нему углу другого треугольника.

2. Решить задачи 13, 14.

III. Самостоятельная работа (20 минут).

Учащиеся выполняют дифференцированные задания: на отметку «отлично» задания по карточкам 1 и 2 либо по карточке 3.

Карточка 1

1. а) Начертите равнобедренный треугольник, обозначьте его.

б) Укажите основание треугольника и его боковые стороны; углы при основании и угол, противолежащий основанию.

2. В равнобедренном треугольнике боковая сторона равна 6 см, а основание – 8 см. Найти периметр треугольника.

3*. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметр равен 50 см. Найдите стороны треугольника.

Карточка 2

1. а) Укажите все равнобедренные треугольники, изображенные на рисунке.

б) Для одного треугольника укажите его основание и боковые стороны; углы при основании и угол, противолежащий основанию.

2. В равностороннем треугольнике сторона равна 7 см. Вычислите периметр треугольника.

3*. В равнобедренном треугольнике основание в три раза больше боковой стороны, а периметр равен 60 см. Найдите стороны треугольника.

Карточка 3 (для более подготовленных учащихся)

1. Сформулируйте и докажите свойство углов равнобедренного треугольника.

2. Равносторонний и равнобедренный треугольники имеют общее основание. Периметр равностороннего треугольника равен 36 см, а периметр равнобедренного треугольника равен 40 см. Найдите стороны данных треугольников.

IV. Итог урока.

– Что такое равнобедренный треугольник?

– Что такое равносторонний треугольник?

– Чем отличается основание от боковых сторон?

– Какими свойствами обладают равнобедренные и равносторонние треугольники?

Задание на дом: пункт 23 с доказательством теоремы об углах при основании в равнобедренном треугольнике, задача 15.

Урок 28
Обратная теорема

Цели: ввести понятие обратной теоремы, доказать ее, научить применять ее на практике.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Анализ самостоятельной работы.

III. Проверка домашнего задания.

1. Один из учащихся оформляет теорему с доказательством.

2. Второй учащийся решает задачу из самостоятельной работы под номером 3* (любого варианта).

IV. Изучение нового материала.

1. Сформулировать обратную теорему: если в треугольнике два угла равны, то треугольник равнобедренный.

2. Учащиеся самостоятельно читают п. 24, выполняют чертеж к теореме и доказывают ее. Доказательство записывается одним учащимся на доске.

V. Закрепление нового материала.

1. Решение задач по готовым чертежам.

Доказать, что DАВС – равнобедренный.

Дано: BD = ВЕ.

2. Решение задач 16, 17.

VI. Итоги урока.

– Что такое обратная теорема?

– Для любой ли теоремы можно сформулировать и доказать обратную ей теорему?

Задание на дом: пункт 24 с доказательством обратной теоремы; задача 18.

Урок 29
Решение задач

Цель: систематизировать знания в ходе решении задач.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Проверка домашней работы.

III. Устная работа.

Решение задач по готовым чертежам.

1. Найти пары равных треугольников.

Дано: АС = ВС.

2. Доказать, что DАВС  – равнобедренный.

IV. Решение задач.

Задача 1.

Дано: АМ^ВМ, ВК^АК, ОК = ОМ.

Доказать: ÐАВК = ÐВАМ. 

Задача 2.

Треугольник АВС – равнобедренный, АВ – его основание, отрезки СО и СН равны. Докажите, что DОАВ = DHBA.

Задача 3.

Периметр равнобедренного треугольника равен 45 см. Найдите его основание, оно больше боковой стороны на 3 см.

V. Итог урока.

Повторить все термины, которые встречались при решении задач.

Задание на дом: повторить весь пройденный материал; решить задачу 49.

Дополнительная задача.

В равностороннем треугольнике DЕК из середины стороны DЕ проведен перпендикуляр МО к стороне DК. Найдите углы треугольника КМО.

Урок 30
Высота, биссектриса
и медиана треугольника

Цели: ввести понятия медианы, биссектрисы и высоты треугольника; научить строить медианы, биссектрисы и высоты треугольника.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Изучение нового материала.

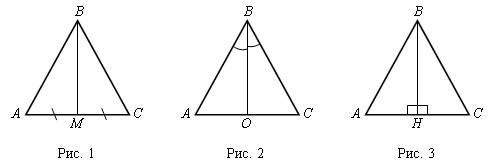
1. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

На доске и в тетрадях рисунок 1 и запись:

АМ – медиана DАВС, если ВМ = МС, где М Î ВС.

2. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

На доске и в тетрадях рисунок 2 и запись:

ВО – биссектриса DАВС, если ÐАВО = ÐСВО, где О Î АС.

3. Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

На доске и в тетрадях рисунок 3 и запись:

ВН – высота DАВС, если ВН ^ АС, Н Î АС.

III. Практическая работа.

Для закрепления навыков построения можно выполнить следующие задания. Учитель просматривает, насколько правильно выполняются задания,  и оказывает необходимую помощь.

Задание 1. Начертить любой треугольник, дать ему название и провести медианы; сделать соответствующие записи.

Задание 2. Начертить любой треугольник, дать ему название и провести биссектрисы углов; сделать соответствующие записи.

Задание 3. Начертить три вида треугольников (прямоугольный, остроугольный и тупоугольный), дать им название и провести высоты в этих треугольниках; сделать соответствующие записи.

IV. Решение задач.

Задача 1.

В равнобедренном треугольнике АВС с основанием ВС проведена медиана АМ. Найдите медиану АМ, если периметр треугольника АВС равен 32 см, а периметр треугольника АВМ равен 24 см.

Оформление данной задачи.

Дано: DАВС, АВ = АС, АМ – медиана.

  Р_DАВС = 32 см, Р_DАВМ = 24 см.

Найти: АМ.

Решение.

1) Р_DАВС = АВ + ВС + АС = 32 см. Так как АВ = АС, ВМ = МС, то ВС = 2ВМ и Р_DАВС = 2(АВ + ВМ) = 32 см, отсюда следует, что АМ + ВМ = 16 см.

2) Р_DАВМ = (АВ + ВМ) + АМ = 24 см. Отсюда следует, что АМ = 24 – 16 = 8 см.

Ответ: АМ = 8 см.

Задача 2.

На рисунке 1 АВ = ВС, Ð1 = 130°.

Найдите угол 2.

V. Итог урока.

– Какими свойствами обладают медианы, биссектрисы и высоты треугольника?

Задание на дом: пункт 25; ответить на вопросы 8, 9, 10; решить задачу 19.

Дополнительные задачи.

1. АС – биссектриса ÐА равнобедренного треугольника АВD. Докажите, что DВАС = DDАА.

2*. В треугольнике АСD проведены медианы АЕ, СВ и DК. Длины отрезков АК, ВD и СЕ соответственно равны 4 см, 3 см и 2 см. Найдите периметр треугольника АСD.

Урок 31
Свойство медианы равнобедренного треугольника

Цели: изучить свойство биссектрисы (медианы, высоты) равнобедренного треугольника, проведенной к основанию; научить применять это свойство при решении задач.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Проверка домашнего задания.

1. Опрос (вопросы в конце параграфа учебника).

2. Проверка решения дополнительных задач.

III. Изучение нового материала.

1) Сформулировать теорему: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и медианой.

2) Доказать теорему, привлекая к этому учащихся.

IV. Решение задач.

1. Задачи 21, 22, 24, 27.

2. Дополнительная задача.

Найти углы треугольника КЕС, если КЕ – медиана равнобедренного треугольника СDЕ с основанием DС, ÐCED = 88°, ÐD = 46°.

V. Итог урока.

– Что такое медиана?

– Какими свойствами обладает равнобедренный треугольник?

– Что такое биссектриса, высота?

– Обладает тем же свойством равносторонний треугольник? Объясните свой ответ.

Задание на дом: пункт 26, выучить доказательство теоремы; задачи 25, 26.

Дополнительная задача.

Дано: АD = СD, ÐМВА = 140°,

 ÐВАК = 110°.

Найти углы треугольника BCD.

Урок 32
Свойство медианы равнобедренного треугольника

Цели: закрепить знания о свойстве биссектрисы (медианы, высоты) равнобедренного треугольника, проведенной к основанию; развивать логическое мышление.

Ход урока

I. Организационный момент.

Сообщение темы урока, формулировка цели.

II. Решение задач.

Дано: DDEК – равнобедренный.

  EF – биссектриса.

  DK = 16 см,  ÐDEF = 43°.

Найти: KF, ÐDEК, ÐEFD.

2. MNK – равнобедренный, точки А и В – середины боковых сторон. Соедините их с точкой D, взятой на медиане NO, и докажите, что DАDN = DBDN.    

3. На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и ВК. ВО – медиана треугольника. Докажите, что DКВО = DМВО.

III. Самостоятельная работа.

Цель: проверить уровень усвоения теоретических знаний, умение применять их при решении задач (второй номер в карточке соответствует уровню трудности).

Карточка 1.3

1. Сформулируйте и докажите свойство углов равнобедренного треугольника.

2. BD – биссектриса равнобедренного треугольника ABC с основанием AC. Найдите ее длину, если периметр треугольника ABC равен 50 см, а периметр треугольника ABD равен 30 см.

Карточка 2.4

1. Сформулируйте и докажите признак равнобедренного треугольника.

2. В треугольнике ABC проведена медиана BD, причем  AD = BD = DC. Найдите ÐDCВ, если ÐАВС = 90°, ÐВАD = 47°. 

Карточка 3.4

1. Сформулируйте  и докажите свойство медианы равнобедренного треугольника.

2. Равносторонний и равнобедренный треугольники имеют общее основание. Периметр равностороннего треугольника равен 36 см, а периметр равнобедренного треугольника – 40 см. Найдите стороны данных треугольников.

Карточка 4.5

1. Сформулируйте и докажите утверждение, обратное следующему: Если углы, смежные с углами одной из сторон треугольника, равны, то данный треугольник – равнобедренный.

2. Основание равнобедренного треугольника равно 8 см. Медиана, проведенная из вершины при основании, делит треугольник на два треугольника, периметр одного из которых на 2 см больше другого. Найдите боковую сторону треугольника.

IV. Итог урока.

– С какими свойствами равнобедренного треугольника вы знакомы? Сформулируйте эти свойства.

Задание на дом: пункт 26, задача 23.

Урок 33
Решение задач

Цель: закрепить полученные знания при решении задач.

Ход урока

I. Организационный момент.

II. Анализ самостоятельной работы.

Рассмотреть типичные ошибки, показать правильное решение.

III. Решение задач.

1. DВND = DFОМ, МО = 8 дм, ÐD = 104°. Найдите длину стороны ND и градусную меру угла М.

2. На луче ОС отмечена точка К. Найдите длину отрезка СК, если ОС = 18,7 см, ОК = 10,5 см.

3. Треугольник АВС – равнобедренный, М и Н – середины боковых сторон. Соедините их с точкой D, взятой на медиане ВО, и докажите, что треугольник МDВ равен треугольнику НDВ.

4. В треугольнике АВС биссектрисы АМ и ВК равны и отсекают на сторонах равные отрезки АК и ВМ. Докажите, что треугольник АВС – равнобедренный.

IV. Итог урока.

Задание на дом: повторить два признака равенства треугольников; пункт 26; задача 24.

Урок 34
Третий признак равенства треугольников

Цели: доказать третий признак равенства треугольников; научить применять данный признак при решении задач.

Ход урока

I. Организационный момент.

Сообщение темы урока, формулировка цели.

II. Анализ самостоятельной работы.

Задачи, которые вызвали затруднение, можно разобрать с подробным решением.

III. Изучение нового материала.

1. Вспомнить первый и второй признаки равенства треугольника.

2. Сформулировать третий признак (по трем сторонам): Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

3. Доказать данную теорему в соответствии с учебником.

IV. Закрепление нового материала. Решение задач.

1. В равнобедренных треугольниках АОВ и СОВ равны основания АВ и ВС. Докажите, что треугольник АОВ равен треугольнику СОВ.

2. Разобрать задачу 29, решенную в учебнике.

3. Решить задачи по чертежам. Найти равные треугольники и доказать их равенство.

4. Решение задачи 30.

V. Итог урока.

– В чем отличие и сходство трех признаков равенства треугольников?

Задание на дом: пункт 27, выучить теорему с доказательством, повторить предыдущий материал, подготовиться к устному опросу; решить задачи 31, 37.

Урок 35
Третий признак равенства треугольников

Цели: закрепить изученный материал; совершенствовать навыки решения задач; развивать логическое мышление.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Самостоятельная работа.

Эта работа проводится по карточкам, второй номер в карточке соответствует уровню трудности.

Карточка 1.3

1. Отметьте на рисунке соответственно равные элементы треугольников так, чтобы можно было записать равенство данных треугольников по третьему признаку равенства треугольников. Выполните записи.

2. В треугольнике АВС АВ = 7 см, ВС = 8 см, АС = 6 см. В треугольнике DКН DК = 7 см, КН = 6 см, DН = 8 см. Докажите равенство треугольников.

Карточка 2.3

1. Начертите два треугольника. Отметьте соответственно равные элементы треугольников так, чтобы можно было записать равенство данных треугольников по третьему признаку равенства треугольников. Выполните записи равных элементов и равенства треугольников.

2. На рисунке АВ и АD, ВС и СD – соответственно равные стороны треугольников АВС и АDС. Докажите равенство данных треугольников.

Карточка 3.4

1. На рисунке изображены равные треугольники. Сформулируйте признак, по которому равны эти треугольники. Выполните записи равных элементов и равенства треугольников.

2. Внутри равнобедренного треугольника АВС (АВ = ВС) отмечена точка О так, что АО = СО. Докажите, что DАОС = DВОС.

Карточка 4.4

1. Сформулируйте третий признак равенства треугольников. Какие аксиомы используются при доказательстве этого признака?

2. Внутри равностороннего треугольника АВС отмечена точка О так, что АО = ВО = СО. Докажите, что DАОС = DВОС = DВОА.  

Карточка 5.5

1. Сформулируйте и докажите третий признак равенства треугольников.

2. На боковых сторонах равнобедренного треугольника во внешнюю сторону построены равносторонние треугольники. Докажите, что отрезки, соединяющие вершины равностороннего треугольника (отличные от вершин равнобедренного треугольника) с серединой основания равнобедренного треугольника, равны.

 

III. Решение задач.

1. В треугольнике АВС и КРМ АВ = КР, ВС = РМ, ÐВ = ÐР. На сторонах АВ и КР отмечены точки D и О так, что ÐАCD = ÐКМО. Докажите, что DАСD = DКМО.

2. Решение задачи с подробным оформлением.

Дано: DАВС, DКРМ, АВ = КР, ВС = РМ, ÐВ = ÐР, D Î АВ, О Î КР, ÐАCD = ÐКМО.

Доказать: DВСD = DРМО.

Решение.

1) DАВС = DКРМ по двум сторонам и углу между ними (АВ = КР, ВС = РМ и ÐВ = ÐР (по условию). Отсюда следует, что ÐАCВ = ÐКМР.

2) ÐВCD = ÐАСВ – ÐАСD, ÐРМО = ÐКМР – ÐКМО.   

Так как ÐАСВ = ÐКМР и ÐАСD = ÐКМО (по условию), то ÐВСD = ÐРМО.

3)  по стороне и прилежащим к ней углам (ВС = РМ, ÐВ = ÐР, ÐВCD = ÐРМО), что и требовалось доказать.

3. Решить задачи 34, 35.

IV. Итог урока.

1. Сформулировать третий признак равенства  треугольника.

2. Даны два треугольника АВС и КЕН. Равенство каких элементов должно выполняться для того, чтобы эти треугольники были равны по одному из 3 признаков (3 случая)? Должно быть три ответа, так как три признака равенства треугольников.

Задание на дом: пункт 27, прочитать пункт 28; решить задачи 38, 40.

Дополнительная задача.

Треугольники АВС и АОС – равнобедренные с общим основанием. Точки В и О лежат в разных полуплоскостях относительно прямой АС. Докажите равенство треугольников АОВ и СОВ.

Урок 36
Решение задач

Цель: закрепить полученные знания при решении задач.

Ход урока

I. Организационный момент.

II. Анализ самостоятельной работы.

Объявить оценки и разобрать ошибки.

III. Решение задач.

1. Отрезки АВ и СD пересекаются в точке О и делятся ею пополам. Докажите, что АС = ВD.

2. В треугольнике АВС АВ = ВС, ВН – медиана, угол АВН равен 25°. Найдите угол АВС.

3. ∆АКТ = ∆ВSМ, ÐТ = 28°,  см. Найдите градусную меру угла и длину стороны АК.

4. Точка P лежит на прямой МК между точками М и К. Найдите длину отрезка МК, если РМ = 12 см, РК = 2 см.

5. а) Найдите градусные меры углов КМЕ и DММ.

б) Постройте угол FOP, равный 85°, начертите угол, смежный с углом FOP, и вычислите его градусную меру.

V. Итог урока.

Задание на дом:

1. В треугольнике АВС АВ = ВС, ВМ – медиана, угол АВС = 110°. Найдите угол АВМ.

2. а) Найдите градусные меры углов АОС и СОВ.

б) Постройте угол MDE, равный 150°, начертите угол, смежный с углом MDE, и вычислите его градусную меру.

Урок 37
Контрольная работа № 3 по теме
«Признаки равенства треугольников»

Цель: проверить знания, умения и навыки учащихся по данной теме.

Ход урока

I. Организационный момент.

II. Выполнение контрольной работы.

Вариант 1

1. Отрезки МК и OD пересекаются в точке Е и делятся ею пополам. Докажите, что МО = DK.

2. В DАNС AN = CN, NE – медиана, ÐCNE = 35°. Найдите ÐАNС.

3. Периметр равнобедренного треугольника равен 15,6 см. Его основание больше боковой стороны на 3 см. Найдите стороны треугольника.

Вариант 2

1. МР = NK и MN = PK. Докажите, что ÐМРК = ÐMNK.

2. В DDFL DF = FL, FC – медиана, ÐDFL = 130°. Найдите ÐCFL.

3. Периметр равнобедренного треугольника равен 13 см. Сумма основания и боковой стороны 8,3 см. Найдите стороны треугольника.

III. Задание на дом.

Повторить дома изученный материал, подготовиться к зачету по теме «Признаки равенства треугольников», который будет проводиться в письменной форме во внеурочное время.

Для подготовки к зачету ответить на вопросы учебника к § 2, 3.

Задания для подготовки к зачету № 2

1. Сторона АВ треугольника АВС равна 25 см, сторона АС меньше АВ на 10 см, а сторона ВС вдвое больше стороны АС. Найдите периметр треугольника АВС.

2. а) Треугольники АВС и КМО равны. На рис. 1 укажите равные элементы этих треугольников, не отмеченные на рисунке.

б) Треугольники АВС и СDА равны (рис. 2), АВ = СD, ВС = АD. Выпишите пары равных углов этих треугольников.

в) Треугольники КМО и DРО равны (рис. 3); ÐМ = ÐР. Выпишите пары равных сторон этих треугольников.

3. На рис. 4 отмечены равные элементы треугольников АСО и ОВD. Равны ли эти треугольники? Почему?

4. На рис. 5 отмечены равные элементы треугольников АВС и АВD. Равны ли эти треугольники? Почему?

5. Дан четырехугольник МВКС, где МК – биссектриса ÐВМС. Равны ли треугольники МВК и МКС, если а) ÐВМК = ÐСКМ; б) МВ = МС? Почему?

6. В равнобедренном треугольнике АВС (рис. 6) АС – основание, Ð2 = 40°. Чему равны углы 1, 3, 4?

Зачет № 2 по теме «Признаки равенства треугольников»

Вариант 1

Обязательная часть.

1. Периметр равнобедренного треугольника равен 66 см, боковая сторона – 20 см. Найдите основание этого треугольника.

2. В равнобедренном треугольнике АВС с основанием АС Ð2 = 38°. Чему равны углы 1, 3 и 4 (рис. 1)?

3. В треугольнике АОС и DОВ АО = ОD и СО = ОВ (рис. 2). Докажите, что треугольники АОС и DОВ равны.

4. В равнобедренном треугольнике АВС с основанием АС ÐС = 40°, ÐВ = 100°. ВК – биссектриса треугольника АВС (рис. 3). Определите углы треугольника АВК.

Дополнительная часть.

5. Треугольники АВС и ВСD – равнобедренные с общим основанием ВС (рис. 4). Верно ли, что ÐАВD = ÐАСD? Почему?

6. Диагонали четырехугольника АВСD делятся в точке пересечения пополам (рис. 5). Выпишите все пары равных треугольников и объясните свой ответ.

Вариант 2

Обязательная часть.

1. Периметр равнобедренного треугольника равен 46 см, основание – 20 см. Чему равна его боковая сторона?

2. В равнобедренном треугольнике АВС с основанием АС Ð2 = 36°. Чему равны углы 1, 3 и 4 (рис. 1)?

3.  В  треугольнике  АОС  и  АВС  ÐОАС = ÐВАС  и  ÐОСА = ÐВСА  (рис. 2). Докажите, что треугольники АОС и АВС равны.

4. В равнобедренном треугольнике с основанием АС ÐС = 50°, ÐВ = 80°. ВК – биссектриса треугольника АВС (рис. 3). Определите углы треугольника АВК.

Дополнительная часть.

5. Треугольники АВС и СDЕ – равнобедренные, АВ = ВС, СD = DЕ (рис. 4). Верно ли, что ÐА = ÐЕ? Почему?

6. Диагонали четырехугольника АВСD делятся в точке пересечения пополам (рис. 5). Выпишите все пары равных треугольников и объясните свой ответ.

Урок 37
Контрольная работа № 3 по теме
«Признаки равенства треугольников»

Цель: проверить знания, умения и навыки учащихся по данной теме.

Ход урока

I. Организационный момент.

II. Выполнение контрольной работы.

Вариант 1

1. Отрезки МК и OD пересекаются в точке Е и делятся ею пополам. Докажите, что МО = DK.

2. В DАNС AN = CN, NE – медиана, ÐCNE = 35°. Найдите ÐАNС.

3. Периметр равнобедренного треугольника равен 15,6 см. Его основание больше боковой стороны на 3 см. Найдите стороны треугольника.

Вариант 2

1. МР = NK и MN = PK. Докажите, что ÐМРК = ÐMNK.

2. В DDFL DF = FL, FC – медиана, ÐDFL = 130°. Найдите ÐCFL.

3. Периметр равнобедренного треугольника равен 13 см. Сумма основания и боковой стороны 8,3 см. Найдите стороны треугольника.

III. Задание на дом.

Повторить дома изученный материал, подготовиться к зачету по теме «Признаки равенства треугольников», который будет проводиться в письменной форме во внеурочное время.

Для подготовки к зачету ответить на вопросы учебника к § 2, 3.

Задания для подготовки к зачету № 2

1. Сторона АВ треугольника АВС равна 25 см, сторона АС меньше АВ на 10 см, а сторона ВС вдвое больше стороны АС. Найдите периметр треугольника АВС.

2. а) Треугольники АВС и КМО равны. На рис. 1 укажите равные элементы этих треугольников, не отмеченные на рисунке.

б) Треугольники АВС и СDА равны (рис. 2), АВ = СD, ВС = АD. Выпишите пары равных углов этих треугольников.

в) Треугольники КМО и DРО равны (рис. 3); ÐМ = ÐР. Выпишите пары равных сторон этих треугольников.

3. На рис. 4 отмечены равные элементы треугольников АСО и ОВD. Равны ли эти треугольники? Почему?

4. На рис. 5 отмечены равные элементы треугольников АВС и АВD. Равны ли эти треугольники? Почему?

5. Дан четырехугольник МВКС, где МК – биссектриса ÐВМС. Равны ли треугольники МВК и МКС, если а) ÐВМК = ÐСКМ; б) МВ = МС? Почему?

6. В равнобедренном треугольнике АВС (рис. 6) АС – основание, Ð2 = 40°. Чему равны углы 1, 3, 4?

Зачет № 2 по теме «Признаки равенства треугольников»

Вариант 1

Обязательная часть.

1. Периметр равнобедренного треугольника равен 66 см, боковая сторона – 20 см. Найдите основание этого треугольника.

2. В равнобедренном треугольнике АВС с основанием АС Ð2 = 38°. Чему равны углы 1, 3 и 4 (рис. 1)?

3. В треугольнике АОС и DОВ АО = ОD и СО = ОВ (рис. 2). Докажите, что треугольники АОС и DОВ равны.

4. В равнобедренном треугольнике АВС с основанием АС ÐС = 40°, ÐВ = 100°. ВК – биссектриса треугольника АВС (рис. 3). Определите углы треугольника АВК.

Дополнительная часть.

5. Треугольники АВС и ВСD – равнобедренные с общим основанием ВС (рис. 4). Верно ли, что ÐАВD = ÐАСD? Почему?

6. Диагонали четырехугольника АВСD делятся в точке пересечения пополам (рис. 5). Выпишите все пары равных треугольников и объясните свой ответ.

Вариант 2

Обязательная часть.

1. Периметр равнобедренного треугольника равен 46 см, основание – 20 см. Чему равна его боковая сторона?

2. В равнобедренном треугольнике АВС с основанием АС Ð2 = 36°. Чему равны углы 1, 3 и 4 (рис. 1)?

3.  В  треугольнике  АОС  и  АВС  ÐОАС = ÐВАС  и  ÐОСА = ÐВСА  (рис. 2). Докажите, что треугольники АОС и АВС равны.

4. В равнобедренном треугольнике с основанием АС ÐС = 50°, ÐВ = 80°. ВК – биссектриса треугольника АВС (рис. 3). Определите углы треугольника АВК.

Дополнительная часть.

5. Треугольники АВС и СDЕ – равнобедренные, АВ = ВС, СD = DЕ (рис. 4). Верно ли, что ÐА = ÐЕ? Почему?

6. Диагонали четырехугольника АВСD делятся в точке пересечения пополам (рис. 5). Выпишите все пары равных треугольников и объясните свой ответ.

Урок 39
Углы, образованные при пересечении
двух прямых секущей

Цели: ввести понятия секущей, внутренних односторонних и внутренних накрест лежащих углов; научить находить эти углы на рисунках.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Актуализация знаний.

Один из учеников у доски доказывает теорему о параллельных прямых, после чего проводится  коллективное обсуждение.

III. Изучение нового материала.

1. Прочитать пункт 30, сделав устные выводы.

2. Записать в тетрадь под диктовку определения.

АВ, СD – прямые, АС – прямая, которая пересекает эти две прямые, называется секущей.

Дать определения внутренних односторонних (углы 1 и 2), внутренних накрест лежащих (углы 2 и 3) углов. Указать на рисунке вертикальные и смежные углы.

Пара углов 2 и 3, пара углов 1 и 2 имеют один общий угол 2 и два других смежных.

Если внутренние накрест лежащие углы равны, то сумма внутренних односторонних углов равна 180°.

Верно и обратное.

Если сумма внутренних односторонних углов равна 180°, то внутренние накрест лежащие углы равны.

3. Решение задач по готовым чертежам.

Найти внутренние односторонние углы и внутренние накрест лежащие. Найти их градусную меру.

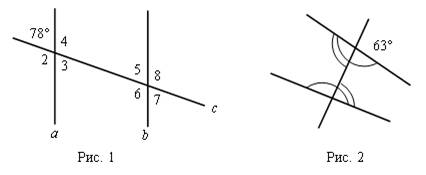
IV. Решение задач.

1. Определите, есть ли на рис. 3 параллельные прямые. Ответ обоснуйте.

Карточка 1

Докажите (см. рис. 4): NK || AC, MN || BC.

Доказательство: DMNK = DBCA по двум сторонам и углу между ними. ÐК = ÐА, следовательно, NK = АС. ÐМ = ÐВ, следовательно, MN || BC.

Карточка 2

Дано (см. рис. 5): АВ = ВС, ЕD = АЕ, ÐС = 80°, ÐLFC = 40°.

Доказать: ED || AC.

Доказательство:  ÐС = ÐВАС = 80°,  так  как  DАВС – равнобедренный (АВ = ВС),  ÐDAC  =  40°,  тогда  ÐЕАD  =  40°.  АЕ = ЕD,  тогда  ÐЕDА = ÐЕАD = 40°. Так как ÐEDA = ÐEAD , то ED || АС.

Карточка 3

Дано  (см.  рис.  3):  ВD = ВЕ,  DС – биссектриса ÐADЕ, ÐBDE = 70°, ÐADE = 55°.

Доказать: DE || AC.

Доказательство:  ÐВDE = 70°, тогда ÐЕDА = 110°.  DС – биссектриса ÐADЕ, тогда ÐЕDС = 55°. ÐЕDС = ÐDСС = 55°, тогда DC || AC.

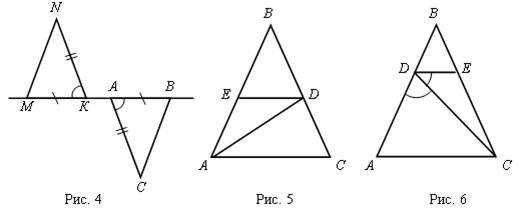
Три ученика у доски решают эти задачи самостоятельно, остальные учащиеся в это время решают задачи 6, 7 по учебнику.

V. Итог урока.

– Что такое параллельные прямые?

– Какими свойствами обладают параллельные прямые?

– С какими новыми углами мы познакомились и как они связаны с параллельными прямыми?

Задание на дом: пункт 30, вопрос 3, задача 5.

Дополнительная задача (см. рис 7).

Дано: Ð1 = Ð2 = Ð3.

Доказать: a || b, m || n.

Урок 40
Признак параллельности прямых

Цели: доказать признак параллельности прямых; научить применять его при решении задач, развивать логическое мышление.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Проверка домашнего задания.

Вынести на доску доказательство вопроса 3.

III. Изучение нового материала.

1. Сформулировать теорему (признак параллельности прямых): Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны.

2. Прочитать доказательство в учебнике и рассмотреть, совпадает ли оно с домашним заданием, после чего записать доказательство в тетрадь.

3. Записать следствие 1: Две прямые, перпендикулярные третьей, параллельны.

4. Ввести определение соответственных углов.

Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами.

Угол 1 и угол 3 соответственные.

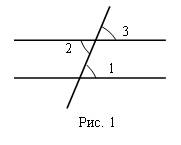
5. Записать следствие 2: Прямые параллельны, если соответственные углы равны.

6. Записать вывод: через точку, не лежащую на данной прямой, можно провести параллельную ей прямую, и только одну.

IV. Закрепление нового материала.

Тест на проверку усвоения теоретических знаний. В результате получения правильных ответов получится имя знаменитого древнего ученого. Ключевое слово – Пифагор.

1. Планиметрия – это наука...

а) о плоских фигурах (Ф);

б) объемных фигурах (К);

в) геометрических терминах (Р).

2. Пересекающиеся прямые...

а) имеют одну общую точку (О);

б) не имеют ни одной общей точки (Р);

в) имеют много общих точек (Н).

3. Два отрезка называются параллельными, если они…

а) оба не перпендикулярны третьей прямой (П);

б) лежат на параллельных прямых (А);

в) не пересекаются на плоскости (Р).

4. Найдите верное утверждение на рисунке 1:

а) Ð2 и Ð3 – вертикальные (Г);

б) Ð1 и Ð3 – внутренние накрест лежащие (А);

в) Ð1 и Ð3 – внутренние односторонние (П).

5. Найдите верное утверждение на рисунке:

а) Ð1 и Ð3 – соответственные (П);

б) Ð1 и Ð2 – смежные (М);

в) Ð1 и Ð2 – вертикальные (Л).

6. Прямые не параллельны, если при пересечении двух прямых секущей…

а) соответственные углы не равны (И);

б) сумма соответственных углов равна 180° (Л);

в) сумма смежных углов не равна 180° (В).

7. Прямые a и b параллельны, если …

а) внутренние накрест лежащие углы равны (Р);

б) они имеют одну общую точку пересечения (А);

в) они лежат в одной плоскости (Ш).

V. Решение задач.

1. Дополнительная задача (см. рис. 2).

Дано: Ð1 = 83°, Ð2 больше Ð1 на 14°.

Параллельны ли прямые MN и сторона АВ?

2. Решить задачу 8.

VI. Итоги урока.

– Сформулируйте признак параллельности прямых.

– В чем заключается смысл следствий из признака параллельности прямых?

– Кто такой Пифагор?

– Какие еще ученые известны вам?

Задание на дом: пункт 31, задача 9.

Урок 41
Признак параллельности прямых

Цели: систематизировать знания о параллельности прямых; научить применять их при решении задач; развивать логическое мышление.

Ход урока

I. Организационный момент.

– Запишите тему и цели урока.

II. Решение задач.

1. Устное решение задач по готовым чертежам.

Доказать, что а || b.                   Доказать, что a || с.

2. Решить задачу 10.

III. Самостоятельная работа.

Вариант 1

1. Параллельны ли прямые d и с, изображенные на рис. 1?

2. Дано: EO = LO, FO = KO. Доказать: EF || KL (рис. 2).

Вариант 2

1. Параллельны ли прямые m и n, изображенные на рис. 1?

2. Дано: NF = PF, MF = QF. Доказать: MN || PQ (рис. 2).

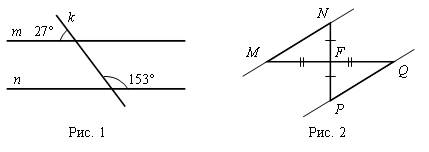
IV. Итог урока.

Задание на дом: пункт 31, задача 11.

Дополнительная задача.

Прямая MN является секущей для прямых AB и CD (М Î АВ, N Î CD). Угол AMN равен 78°. При каком значении угла CNM прямые AB и CD могут быть параллельными?

Урок 42
Свойство углов, образованных при пересечении
параллельных прямых секущей

Цели: познакомить учащихся со свойствами углов, полученных при пересечении прямых секущей; научить применять это свойство при решении задач; систематизировать знания учащихся о свойствах параллельных прямых; развивать логическое мышление.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Анализ самостоятельной работы.

Объявить результаты, решить задачу, с которой не справились учащиеся.

III. Проверка домашней работы.

1. Выборочная проверка решения дополнительной задачи.

2. Беседа по вопросам в конце параграфа.

IV. Изучение нового материала.

1. Сформулировать обратную теорему: Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.

2. Доказательство предложить прочитать самостоятельно, дать возможность учащимся оформить его в тетради, провести проверку.

3. Записать следствие: Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.

V. Закрепление изученного материала.

Задача 1.

Докажите, что прямые a и b параллельны, Ð1 + Ð2 = 180° (см. рис.).

Задача 2.

Докажите, что прямые MO и PK параллельны, если известно, что отрезки MP и OK пересекаются в точке А и делятся этой точкой пополам.

Решение задач 12, 14 по учебнику

VI. Итоги урока.

– Какими свойствами обладают параллельные прямые?

– Какие углы существуют при пересечении параллельных прямых секущей?

– Что такое секущая?

– Какие прямые называются параллельными?

Задание на дом: пункт 32; задачи 15, 16.

Урок 43
Свойство углов, образованных
при пересечении параллельных прямых секущей

Цели: закрепить знания о свойствах углов, полученных при пересечении прямых секущей; закрепить навыки решения задач на применение этих свойств; развивать логическое мышление.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Самостоятельная работа.

Выполнение дифференцированных заданий. Вторая цифра в номере карточки указывает на уровень трудности этих заданий.

Карточка 1.3

1. Сформулируйте аксиому параллельных прямых.

2. Определите на рисунке пару параллельных прямых при условии, что Ð1 = Ð2. Найдите еще пару равных углов.

Карточка 2.4

1. Докажите, что если две прямые параллельны третьей прямой, то они параллельны.

2. На рисунке d || f, f || h; Ð1 = 24°. Определите градусную меру угла 2 и угла 3.

Карточка 3.4

1. Сформулируйте и докажите свойство внутренних накрест лежащих углов при параллельных прямых.

2. На рисунке ÐАВС = 49° и DK || GC.

Найдите градусную меру углов DAB, KAB, LAK, LAD.

Карточка 4.5

1. Докажите, что две прямые, перпендикулярные третьей прямой, параллельны.

2. Равные отрезки KL и NM лежат на параллельных прямых. КМ – секущая. Докажите, что DKLM = DMNK.

Карточка 5.5

1. Сформулируйте и докажите признак параллельности прямых, используя понятие внутренних накрест лежащих углов.

2. Прямая, параллельная основанию равнобедренного треугольника АВС, пересекает боковые стороны АВ и АС в точках M и N. Докажите, что треугольник DАMN – равнобедренный.

III. Решение задач.

1. Решить задачу 17.

2. Дополнительные задачи.

1) На рисунке прямые а, b параллельны.

а) Найдите величину Ð1, если он больше Ð2 на 44°.

б) Найдите эти углы, если они относятся как 7 : 3.

2) Точки С и Е лежат в разных полуплоскостях относительно прямой ВD, а отрезки ВЕ и СD параллельны и равны. Докажите, что DDBB = DBDC.

IV. Итог урока.

– Какими свойствами обладают углы при пересечении параллельных прямых секущей?

Задание на дом: пункт 32; повторить все ранее доказанные теоремы.

Дополнительная задача.

1) Отрезки ВС и АD пересекаются в точке О. Известно, что прямые АВ и СD параллельны, а отрезки АО и ОВ равны. Докажите, что отрезки СО и ОD тоже равны.

2) В треугольнике АВС проведены биссектриса АК и отрезок МК, причем точка М лежит на стороне АС и МК параллельна АВ. Докажите, что треугольник АМК – равнобедренный.

Урок 44
Сумма углов треугольника

Цели: доказать теорему о сумме углов треугольника, ее следствие; научить применять данную теорему при решении задач.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Анализ самостоятельной работы.

Проанализировать ошибки, допущенные при решении самостоятельной работы. Выполнить работу над ошибками.

III. Изучение нового материала.

1. Решение задачи по готовому чертежу устно; рисунок сделать на доске.

На рисунке BD || AC. Найдите сумму углов треугольника.

2. Постановка проблемы: всегда ли сумма углов в треугольнике равна 180°?

3. Формулировка теоремы (о сумме углов в треугольнике): сумма углов в треугольнике равна 180°.

4. Самостоятельное изучение доказательства теоремы по учебнику.

5. Запись следствия из теоремы: у любого треугольника хотя бы два угла острые.

6. Введение понятия остроугольного, тупоугольного, прямоугольного треугольника.

IV. Практическое задание.

Нарисовать каждый треугольник. При помощи транспортира проверить справедливость теоремы.

V. Закрепление нового материала.

1. Решение задач по готовым чертежам.

2. Решение задач 18, 22 по учебнику.

V. Итог урока.

1. Могут ли в треугольнике быть:

а) два тупых угла; б) тупой и прямой угол; в) два прямых угла?

Ответ объясните.

2. Может ли быть тупой угол при основании равнобедренного треугольника? Ответ поясните.

Задание на дом: пункт 33, доказательство теоремы, вопрос 10, задачи 19, 23.

Урок 45
Сумма углов треугольника

Цели: совершенствовать навыки решения задач; развивать логическое мышление.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Решение задач.

1. Найдите углы при основании равнобедренного треугольника АВС, если угол между боковыми сторонами равен 110°.

2. Докажите, что треугольник АВС – равносторонний, если известно, что ÐА = ÐВ = 60°.

3. Решить задачи 24, 28 из учебника.

III. Самостоятельная работа (15 минут).

Вариант 1

1. В равнобедренном треугольнике один из углов равен 78°. Найдите два других угла этого треугольника.

2. В треугольнике АВС проведена биссектриса АО, ÐВ = 64°, ÐС = 36°. Найти угол АОВ.

Вариант 2

1. Один из углов равнобедренного треугольника равен 142°. Найдите два других угла.

2. В треугольнике АВС проведена биссектриса АО, ÐС = 44°, ÐАОВ = 74°. Найдите угол D.

Вариант 3

1. В равнобедренном треугольнике АВС с основанием АС и ÐВ = 104° проведена высота АК. Найдите ÐВАК.

2. В треугольнике АВС проведены биссектрисы АМ и ВК, пересекающиеся в точке О, причем ÐАОК = 58°. Найдите угол АСВ.

IV. Итог урока.

– Чему равна сумма углов в треугольнике?

– Какие бывают треугольники, от чего это зависит?

Задание на дом: пункт 33, задачи 25, 27.

Урок 46
Внешний угол треугольника

Цели: ввести определение внешнего и внутреннего углов треугольника; доказать теорему о внешнем угле, научить применять данные сведения при решении задач.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Анализ самостоятельной работы.

Объявить результаты, проанализировать допущенные ошибки, можо решить на доске один из вариантов.

III. Актуализация знаний.

1. Один из учащихся доказывает теорему о сумме углов треугольника.

2. Второй ученик решает у доски задачу 29.

3. Фронтальный опрос.

– Что такое развернутый угол?

– Назовите известные углы.

– Что такое смежный угол?

– Какие бывают треугольники, какими свойствами они обладают?

4. Решение задачи по готовым чертежам (устно). Найти все неизвестные углы.

 

IV. Изучение нового материала.

1. Ввести понятие внешнего угла.

Внешним углом треугольника называется угол при данной вершине, смежный с углом треугольника при этой вершине.

2. Сформулировать теорему о внешнем угле: внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

3. Доказательство теоремы в соответствии с учебником.

4. Записать следствие из теоремы: внешний угол треугольника больше любого внутреннего угла, не смежного с ним.

5. Разобрать решенную задачу 35 по учебнику.

6. Решить задачу по готовому чертежу.

Найти внутренние углы треугольника КМР и внешний угол МРА.

V. Решение задач.

1. Решить задачи 32, 34 по учебнику.

2. Дополнительная задача.

Найти неизвестные углы треугольников.

VI. Самостоятельная работа.

Вариант 1 (на «3»)

Найдите углы равнобедренного треугольника, если угол при основании в два раза больше угла, противолежащего основанию.

Оформление решения.

Дано: DАВС, АВ = ВС.

  ÐА < ÐС в два раза.

Найти: ÐА, ÐВ, ÐС.

Решение:

Пусть ÐВ = х, тогда ÐА = ÐС = 2х.

Так как ÐА + ÐВ + ÐС = 180°, то х + х + 2х = 180°, отсюда следует, что х = 36°, то есть ÐВ = 36°, ÐА = ÐС = 72°.

Ответ: 36°, 72°, 72°.

Вариант 2 (на «4» и «5»)

Найдите углы равнобедренного треугольника, если угол при основании в три раза меньше внешнего угла, смежного с ним.

Оформление решения.

Дано: DАВС, АВ = ВС.

  ÐBCD = 3 ÐС.

Найти: ÐА, ÐВ, ÐС.

Решение:

Пусть ÐС = х, тогда ÐВСD = 3х. Но ÐС + ÐBCD = 180°, так как они смежные, тогда х + 3х = 180°, х = 45°, отсюда следует ÐА = ÐС = 45°, ÐВ = 90°.

Ответ: 45°, 45°, 90°.

Вариант 3 (на «4» и «5»)

Найдите углы треугольника, где АВ = ВС, если угол при основании в 2 раза меньше внешнего угла, смежного с ним.

Оформление решения.

Дано: DАВС, АВ = ВС.

  ÐBCD = 2ÐС.

Найти: ÐА, ÐВ, ÐС.

Решение:

Пусть ÐС = х, тогда ÐBCD = 2х. Но ÐС + ÐBCD = 180°, так как они смежные, тогда х + 2х = 180°, х = 60°, отсюда следует ÐА = ÐС = 60°, ÐВ = 60°. Так как все углы по 60°, то можно сделать вывод, что треугольник равносторонний.

Ответ: 60°, 60°, 60°.

VII. Итоги урока.

– Что такое внешний угол?

– Чем отличается внешний угол от внутреннего угла треугольника?

– Какая максимальная величина может быть у внешнего угла?

Задание на дом: пункт 34, вопросы 11, 13; задачи 33, 35.

Урок 47
Прямоугольный треугольник

Цели: ввести определение прямоугольного треугольника; развивать логическое мышление учащихся.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Самостоятельная работа.

Для получения оценки «3» достаточно ответить на вопросы 1 и 2, содержащих только формулировку.

Вариант 1

1. Сформулируйте и докажите теорему о сумме углов треугольника.

2. Следствие из теоремы о внешнем угле.

3. Найдите неизвестные углы треугольника, если один его угол равен 48°, а один из внешних углов равен 120°.

Вариант 2

1. Сформулируйте и докажите теорему о внешнем угле.

2. Следствие из теоремы о сумме углов треугольника.

3. Найти углы равнобедренного треугольника, если внешний угол при вершине, противолежащий основанию, равен 106°.

III. Изучение нового материала.

1. Дать определение прямоугольного треугольника.

Треугольник называется прямоугольным, если у него есть прямой угол.

2. Нарисовать прямоугольный треугольник, на его примере объяснить, как называются стороны прямоугольного треугольника.

АВ, АС – катеты;

ВС – гипотенуза.

Сторона, лежащая против угла в 90°, называется гипотенузой, две другие называются катетами.

3. Записать признак равенства прямоугольных треугольников: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.

IV. Решение задач.

1. Решить задачи по готовым чертежам.

Необходимо найти равные треугольники.

2. Разобрать решенную задачу 43 по учебнику.

Сделать вывод: катет, лежащий против угла в 30°, равен половине гипотенузы.

3. Решить устно задачи по готовым чертежам.

               Найдите: АВ.               Найдите: ВС.             Найдите: ВС.

4. Решить задачу 41.

V. Итог урока.

– Что такое прямоугольный треугольник?

– Чему равна сумма углов в прямоугольном треугольнике?

– Чему равен катет, лежащий против угла в 30°?

Задание на дом: пункт 35,  вопросы 14–17, задачи 42, 46.

Урок 48
Прямоугольный треугольник

Цели: закрепить знания учащихся о прямоугольном треугольнике при решении задач; развивать логическое мышление.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Устная работа.

Задание: решить задачи по готовым чертежам.

1) Рис. 1. Найти ÐВ.

2) Рис. 2. Найти ÐА, ÐВ, ÐDCB.

Доказать: DАDС и DВDС – равнобедренные.

3) Рис. 3. Найти ÐCАD.

4) Рис. 4. Найти ВС .

5) Рис. 5. Найти АС.

6) Рис. 6. Найти ÐА, ÐС.

III. Анализ проверочной работы.

Указать типичные ошибки, решить одну из задач.

IV. Повторение изученного материала.

1. Провести устный опрос по вопросам в конце параграфа.

2. Решить задачи по готовым чертежам.

                  Найдите: АВ.                            Найдите: АЕ.

V. Решение задач.

1. В треугольнике АВС угол С – прямой. Найдите его острые углы, если угол между высотой СD и катетом ВС равен 37°.

2. АМ и ВК – перпендикуляры к прямой МК. Докажите, что DАОМ = DВОК, если: а) АМ = ВК; б) АО = ВО.

3. Решить задачу 45 по учебнику.

Дополнительные задачи с решением.

1. Найдите углы прямоугольного треугольника, если угол между биссектрисой и высотой, проведенный из вершины прямого угла, равен 15°.

Дано: DАВС, СD – биссектриса,

  СН – высота, ÐDCH = 15°.

Найти: ÐA, ÐВ, ÐС.

Решение:

СD – биссектриса, СН – высота, ÐDCH = 15°, ÐDCA = 45°, тогда ÐHСА = 30°.

DHСА – прямоугольный, в нем ÐНCA = 30°, тогда ÐCAН = 60°. DАВС – прямоугольный, в нем ÐA = 60°, тогда ÐВ = 30°.

Ответ: 60°, 30°, 90°.

2. В равнобедренном треугольнике один из углов 120°, а основание равно 4 см. Найдите высоту, проведенную  к боковой стороне.

Дано: DАВС, АВ = ВС.

  АН – высота, ÐВ = 120°,

  АС = 4 см.

Найти: АН.

Решение:

Так как  ÐВ = 120°, то ÐА = ÐС = 30°. АН – высота DАВС, тогда DАНС – прямоугольный, в нем ÐС = 30°, значит,  = 2 см.

Ответ: 2 см.

3. Высота, проведенная к боковой стороне равнобедренного треугольника, делит пополам угол между основанием и биссектрисой. Найдите углы равнобедренного треугольника.

Дано: DАВС, АВ = ВС,

  АD – биссектриса,

  АН – высота,

  Ð DAN = Ð CAH.

Найти: ÐA, ÐВ, ÐС.

Решение:

AD – биссектриса ÐВАС, АН – высота DАВС, ÐDAН = ÐСАН. Так как АD – биссектриса ÐВАС, то ÐBAD = ÐDAC, но Ð DAC = ÐDAN + ÐСАН, причем ÐDAN = ÐСАН, тогда ÐСАН = ÐВАС.

DАВС – равнобедренный, поэтому ÐBAС = ÐВСА, значит, ÐСАН = ÐВАС.  DАВС – прямоугольный, значит,  ÐСАН +ÐНСА = 90°,  тогда  ÐНСА + ÐНСА = 90°, ÐНСА = 72°, следовательно, ÐВСА = ÐВАС =  72°, ÐАВС =  36°.

Ответ: 72°, 72°, 36°.

VI. Итог урока.

– Сформулируйте признаки равенства треугольников.

– Верны ли они для прямоугольных треугольников, равнобедренных и равносторонних треугольников?

Задание на дом: пункт 35, задачи 44, 46.

Одному из учеников предложить подготовить сообщение на тему «Из истории возникновения геометрии». Можно использовать пункт 37, дополнительную литературу.

Дополнительная задача.

Найдите угол между боковыми сторонами равнобедренного треугольника, если известно, что один из внутренних углов в три раза меньше одного из внешних углов. Укажите три возможных ответа.

Урок 49
Существование и единственность
перпендикуляра к прямой

Цели: доказать теорему о существовании и единственности перпендикуляра к прямой; научить применять данную теорему при решении задач.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Проверка домашней работы.

Проверить решение дополнительной задачи.

III. Сообщение учащегося об истории возникновения геометрии.

IV. Самостоятельная работа.

Оценка зависит от количества правильно выполненных заданий.

Вариант 1

1. СН – высота, проведенная к гипотенузе прямоугольного треугольника АВС с прямым углом С. Найдите угол АСН, если ÐВ = 45°.

2. Дан треугольник МОК, ÐК = 65°, ВС || МК, ВС = ВО. Найти угол О.

3. Найдите угол О треугольника ОКН, если он на 20° больше угла Н, а внешний угол при вершине К равен 108°.

Вариант 2

1. АО – биссектриса прямоугольного треугольника АВС с прямым углом С. Найдите угол ОАС, если .

2. Дан треугольник АВС, угол В равен 80°, ОК || ВС, ОК = ОА. Найдите угол АКО.

3. Найдите угол О треугольника МРО, если он на 40° меньше угла М, а внешний угол при вершине Р равен 122°.

V. Изучение нового материала.

1. Вспомнить определение перпендикуляра.

2. Сформулировать теорему о существовании и единственности перпендикуляра к прямой: из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.

3. Доказать теорему по учебнику.

4. Дать определение длины перпендикуляра: длиной перпендикуляра, опущенного из данной точки на прямую, называется расстояние от точки до прямой.

5. Разобрать решенную задачу 50 по учебнику.

VI. Решение задач.

Решить задачу 49.

VII. Итог урока.

– Что такое перпендикуляр?

– Что называется расстоянием от точки до прямой?

– Объясните, что такое расстояние между параллельными прямыми.

Задание на дом: пункт 36; вопросы 19, 20; задача 48.

Урок 50
Решение задач по теме
«Сумма углов треугольника»

Цели: закрепить знания о сумме углов треугольника; совершенствовать навыки решения задач на применение теорем.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Устная работа.

1. Решение задач по готовым чертежам.

Найти неизвестные углы треугольников.

Дано: АВ || СН.

III. Решение задач.

Задача 1.

Дано: ÐА = 90°; CF, DB – биссектрисы треугольника АСD.

Найти: ÐCOD.

Решение: ÐА = 90°, тогда ÐАСD + ÐАDC = 180° – ÐА = 90°. CF, DB – биссектрисы DАСD, тогда   а .

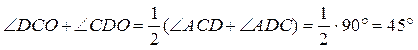В  DСDО  ÐDCO  +   ÐCDO  +  ÐСOD = 180°,  тогда  ÐСOD  =  180° –  (ÐDCO + ÐCDО) = 180° – 45° = 135°.

Ответ: .

Задача 2.

Биссектрисы углов А и В треугольника АВС пересечены в точке М. Найдите ÐАМВ, если ÐА = 58°, ÐВ = 96°.

Задача 3.

Найдите углы равнобедренного треугольника, если: а) угол при основании в два раза больше угла, противолежащего основанию; б) угол при основании в три раза меньше внешнего угла, смежного с ним.

Задача 4.

Медиана АМ треугольника АВС равна половине стороны ВС. Докажите, что треугольник АВС прямоугольный.

Задача 5.

Один из внешних углов равнобедренного треугольника равен 115°.

Найдите углы треугольника.

IV. Итог урока.

Задание на дом: повторить пройденный материал, подготовиться к контрольной работе.

Дополнительная задача.

1. Докажите, что каждый угол равностороннего треугольника равен 60°.

2. Докажите, что углы при основании равнобедренного треугольника острые.

Урок 51
Контрольная работа № 4 по теме
«Сумма углов треугольника»

Цель: проверить знания, умения и навыки учащихся по данной теме.

Ход урока

I. Организационный момент.

II. Выполнение работы.

Вариант 1

1. Параллельные прямые а и b пересекаются прямой с, Ð1 = 123°. Найдите угол 2 (см. рис.).

2. Прямая m пересекает стороны треугольника АВС, АВ в точке Р, ВС в точке Е. ÐАВС = 35°, ÐАСВ = 84°, ÐАРЕ = 119°.

а) Докажите, что прямые m и АС параллельны.

б) Найдите внешний угол треугольника АВС при вершине А.

Вариант 2

1. Прямая k пересекает параллельные прямые m и n, Ð1 = 64°. Найдите угол 2 (см. рис.).

2. Прямая а пересекает стороны треугольника MNK KM в точке А, KN в точке В. ÐMNK = 24°, ÐMKN = 138°, ÐMАВ = 162°.

а) Докажите, что прямые l и MN параллельны.

б) Найдите внешний угол треугольника MNK при вершине M.

III. Задание на дом.

Повторить весь изученный материал, подготовиться к зачету по теме «Сумма углов треугольника. Параллельность прямых», который будет проводиться во внеурочное время.

Для подготовки можно использовать вопросы из учебника после параграфа 4.

Задания для самоподготовки к зачету № 3

1. а) Найдите ÐС треугольника АВС, если ÐА = 39°, ÐВ = 81°.

   б) Один из острых углов прямоугольного треугольника равен 35°. Какова величина второго острого угла?

2. а) В равнобедренном треугольнике угол при вершине, противолежа-щий основанию, равен 75°. Найдите углы при основании этого треугольника.

   б) В равнобедренном треугольнике угол при основании равен 32°. Найдите угол при вершине, противолежащий основанию.

    в) Найдите величину угла при основании прямоугольного равнобедренного треугольника.

    г) Чему равны углы равностороннего треугольника?

3. По рисунку 1 выпишите пары: а) накрест лежащих углов; б) односторонних углов; в) соответственных углов.

4. Докажите, что прямые a и b параллельны (рис. 2), если:

а) Ð1 = Ð2; б) Ð1 = Ð4; в) Ð1 = 105°, Ð3 = 75°.

5. Прямые a и b параллельны (рис. 3). Назовите углы, равные углу 1.

6. По данным на рис. 4 определите угол 1.

7. Параллельны ли прямые а и b (рис. 5), если Ð1 = 48°, Ð2 = 133°.

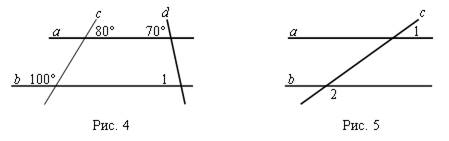
8. На рисунке 6 отмечены равные элементы прямоугольных треугольников. Равны ли эти треугольники? Почему?

9. В равнобедренном треугольнике АВС с основанием АС проведена высота АН (рис. 7). Определите углы треугольника АСН, если ÐВ = 68°.

10. На рисунках 8 и 9 Ð1 = 45°, Ð2 = 65°. Найдите угол 3.

11. Чему равны углы равнобедренного треугольника, если внешний угол при вершине, противолежащей основанию, равен 140°?

12. Проведите произвольную прямую а и отметьте точку М, не лежащую на ней. Найдите расстояние от точки М до прямой а.

13. Проведите две параллельные прямые и найдите расстояние между ними.

Зачет № 3 по теме «Сумма углов треугольника.
Параллельные прямые»

Вариант 1

Обязательная часть.

1. На рисунке 10 определите угол А треугольника АВС.

2. В треугольнике КОМ определите величину внешнего угла при вершине М (рис. 11).

3. В треугольнике АВС, ÐА – прямой, ÐВ = 25°.

 а) Найдите величину угла С.

 б) Укажите больший катет треугольника АВС.

4. Прямые а и b параллельны, Ð1 = 115°. Найдите углы 2 и 3 (рис. 12).

5. По данным на рисунке 13 найдите Ð1.

Дополнительная часть.

6. Определите углы четырехугольника АВСD, если АВ || CD, AD || ВС.

ÐА = 70° (рис. 14).

7. В равнобедренном треугольнике АВС с основанием АС проведена высота АD. Определите углы треугольника АDС, если ÐВ = 70° (рис. 15).

8. Треугольник KMN – равнобедренный с основанием KN. Прямая АВ параллельна стороне MN. Докажите, что треугольник КАВ – равнобедренный (рис. 16).

Вариант 2

Обязательная часть.

1. По рис. 17 определите угол А треугольника АВС.

2. В треугольнике КОМ определите величину внешнего угла при вершине М (рис. 18).

3.  В треугольник АВС ÐА – прямой, ÐВ = 35°.

     а) Найдите величину угла С.

     б) Укажите меньший катет треугольника АВС.

4. Докажите,  что  прямые  a и b параллельны, если Ð1 = 140°, Ð2 = 40° (рис. 19).

5. По данным рис. 20 найдите Ð1.

Дополнительная часть.

6. Отрезки АD и СВ равны и параллельны (рис. 21). Докажите, что треугольники ВDА и АВС равны.

7. В равнобедренном треугольнике АВС с основанием АС проведена высота АD. Определите углы треугольника АВD, если ÐС = 50° (рис. 22).

8. Треугольник КMN – равнобедренный с основанием КN. Прямая АВ параллельна основанию (рис. 23). Докажите, что треугольник АМВ – равнобедренный.

Геометрическое построение

Основная цель: научить решать задачи при помощи циркуля и линейки.

Урок 52
Окружность. Что такое задачи на построение

Цели: систематизировать знания об окружности и ее элементах; ввести понятие о решении задач на построение.

Ход урока

I. Организационный момент.

Сообщение темы и цели урока.

II. Актуализация знаний.

1. Проверить домашнюю задачу с оформлением решения на доске одним из учеников.

2. Объявить результаты самостоятельной работы, выполнить анализ ошибок.

III. Изучение нового материала.

1. Дать определение окружности, центра, радиуса, диаметра и хорды. В тетрадях необходимо записать определения, сделать рисунок и все показать на нем.

Окружность – фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки. Эта точка называется центром окружности.

Расстояние от точки окружности до ее центра называется радиусом.

Отрезок, соединяющий две точки окружности, есть хорда.

Хорда, проходящая через центр, называется диаметром. Диаметр состоит из двух радиусов.

2. Точка О – центр окружности.

Отрезок DК – диаметр, причем DО = ОК = R, отрезок ОВ = R – радиус. Отрезок СА – хорда.

3. Прочитать пункт 42.

– Мы будем заниматься геометрическим построением на плоскости.

Основными инструментами при этом будут односторонняя линейка и циркуль.

4. Запись аксиомы линейки и циркуля.

Аксиомы линейки:

Линейка позволяет выполнить следующие геометрические построения:

а) построить отрезок, соединяющий две построенные точки;

b) построить прямую, проходящую через две построенные точки;

с) построить луч, исходящий из построенной точки и проходящий через другую построенную точку.

Аксиомы циркуля:

Циркуль позволяет выполнить следующие геометрические построения:

а) построить окружность, если построен центр окружности и отрезок, равный радиусу окружности;

b) построить любую из двух дополнительных дуг окружности, если построены центр окружности и концы этих дуг.

IV. Практическая работа.

Задание 1. Построить окружность радиусом 4 см, отметить центр, диаметр, хорду, равную 3,5 см.

Задание 2. В окружности с центром О проведена хорда ВС, причем ÐВОС = 84°. Дополните рисунок и найдите остальные углы треугольника ВОС.

V. Итоги урока.

– Что такое окружность, плоская ли это фигура?

– Что называется радиусом, диаметром, хордой, центром окружности?

– Назвать основные инструменты для решения задач на построение.

Задание на дом: пункты 38, 42; вопросы 1, 2.

Дополнительная задача.

Проведите в окружности с центром  в точке О два диаметра МК и DС. Докажите, что МD = КС.

Урок 53
Касательная к окружности

Цель: ввести понятие касательной, научить применять полученные знания при решении задач.

Ход урока

I. Организационный момент.

Сформулировать тему и цель урока.

II. Анализ практической работы.

III. Изучение нового материала.

1. Дать определение касательной.

2. Начертить окружность и провести различные прямые, попросить определить, где будет касательная (на рисунке должны быть и радиусы, и хорды, и диаметры, и касательные).

IV. Решение задач.

1. Дана окружность с центром О. В данной окружности проведены два диаметра АВ и СD. Докажите, что АС = ВD.

2. К окружности с центром О проведите касательные АВ и СВ. Докажите, что АВ = СВ, а луч ВО – биссектриса угла АСВ.

3. Найдите отрезки касательных АВ и АС, проведенных из точки А к окружности радиуса r, если r = 9 см, а угол ВАС равен 120°.

V. Итоги урока.

Задание на дом: пункт 26.

Дополнительная задача.

Отрезок СD – высота прямоугольного треугольника АВС, проведенная из вершины прямого угла С. Найдите радиус окружности с центром А, которая касается прямой СD, если СD = 4 см, АВ = 12 см.

Урок 54
Окружность, описанная около треугольника

Цель: ввести понятия окружности, описанной около треугольника, научить применять все свойства окружностей при решении задач.

Ход урока

I. Организационный момент.

Сформулировать тему и цель урока.

II. Проверка домашней работы.

III. Изучение нового материала.

Объясняется материал, предложенный в  параграфе учебника.

IV. Решение задач.

1. Дана окружность с центром в точке О, медиана ОС треугольника АВС равна 6 см. Найдите диаметр окружности.

2. DС – касательная к окружности с центром в точке О, В – точка касания, треугольник ВОА – равносторонний. Определите угол АВD.

3. К окружности с центром в точке О проведена касательная DС (В – точка касания). Найдите углы треугольника АОВ если угол АВС равен 129°.

V. Итоги урока.

Задание на дом: пункт 39.

Дополнительные задачи.

1. Радиус окружности с центром в точке О равен 7 см, угол ВАО равен 60°. Найдите хорду АВ.

2. Дана окружность с центром в точке О, медиана ОС треугольника АВС равна 8 см, найдите диаметр окружности.

Урок 55
Окружность, вписанная в треугольник

Цель: ввести понятие окружности, вписанной в любой треугольник, научить применять все свойства окружностей при решении задач.

Ход урока

I. Организационный момент.

Сформулировать тему и цель урока.

II. Объяснение нового материала.

    Объяснение материала можно провести согласно параграфу.

III. Решение задач.

1. Треугольник описан около окружности с центром в точке О, угол САО равен 27°. Чему равен угол ВАО?

2. Треугольник ВАС описан около окружности с центром в точке О. Сравните градусную меру углов в САО и ВАО.

3. DС – касательная к окружности с центром в точке О, В – точка касания, треугольник ВОА – прямоугольный. Определите угол АВD.

IV. Итоги урока.

Задание на дом: пункт 41.

Дополнительные задачи.

1. Дана окружность с центром в точке О. Определите вид треугольника ВОА.

2. В равнобедренный треугольник АВС с основанием АС вписана окружность с центром в точке О. Найдите длины отрезков АМ и МВ, если периметр треугольника равен 38 см, а АВ – 13 см.

Урок 56
Построение треугольника с данными сторонами

Цели: дать представление о задачах на построение; рассмотреть задачу на построение треугольника с данными сторонами, учить работать линейкой и циркулем.

Ход урока

I. Организационный момент.

Сформулировать тему урока, поставить цели.

II. Проверка домашнего задания.

1. Провести опрос учеников по вопросам в конце параграфа.

2. Проверить решение дополнительной задачи.

III. Изучение нового материала.

Задачи на построение – это такие задачи, при решении которых нужно построить геометрическую фигуру, удовлетворяющую условиям задачи, с помощью циркуля и линейки.

Схема решения задач на построение:

1) Анализ (рисунок искомой фигуры, устанавливающий связи между данными задачи и искомыми элементами, и план построения).

2) Построение по намеченному плану.

3) Доказательство, что данная фигура удовлетворяет условиям задачи.

4) Исследование (при любых ли данных задача имеет решение, и если имеет, то сколько).

На доске учитель строит треугольник, объясняя, учащиеся делают записи в тетради.

Построение треугольника по трем сторонам.

Задача. Построить треугольник по трем заданным сторонам.

Описание работы:

1. Выбрать самый большой отрезок, построить его при помощи линейки, дать ему название, в нашем случае это отрезок АВ.

2. Взять циркуль, замерить среднюю сторону, в нашем случае отрезок b, поставить циркуль в точку А и провести окружность радиусом b.

3. Измерить отрезок а, отложить его из точки В, провести окружность радиусом а.

4. На пересечении двух окружностей радиуса а и радиуса b поставить точку, назвать ее буквой С, соединить отрезок АС и отрезок ВС.

5. Получили треугольник с данными сторонами при помощи линейки и циркуля.

IV. Решение задач.

1. Практическая работа выполняется учащимися самостоятельно, при необходимости учитель помогает.

Вариант 1. Задача 19 (1).

Вариант 2. Задача 19 (2).

2. Решить задачу 20.

V. Итоги урока.

Как построить треугольник, если даны три стороны?

Задание на дом: пункт 43; задачи 19 (3), 21.

Урок 57
Построение угла, равного данному

Цели: научить строить угол, равный другому углу, при помощи линейки и циркуля.

Ход урока

I. Организационный момент.

Сформулировать тему и цели урока.

II. Практическая работа.

Вариант 1

Построить треугольник по трем сторонам a, b и c: если a = 3 см, b = 4 см, с = 6 см.

Вариант 2

Построить треугольник по трем сторонам a, b и c: если a = 2 см, b = 6 см, с = 5 см.

III. Изучение нового материала.

1. Прочитать пункт 44.

2. Поставить задачу, сформулировать цель, проговорить порядок действий.

3. Построить угол в тетрадях и на доске.

Задача: отложить от данной полупрямой в данную полуплоскость угол, равный данному углу.

IV. Решение задач.

Задачи 23 (1), 24 (1).

V. Итоги урока.

Задание на дом: пункт 44, задачи 23 (2), 24 (2).

Урок 58
Построение биссектрисы угла.
Деление отрезка пополам

Цели: научить строить биссектрису угла, делить отрезок на две равные части при помощи циркуля.

Ход урока

I. Организационный момент.

Сформулировать тему и цели урока.

II. Анализ практической работы.

Объявить результаты, разобрать типичные ошибки на доске.

III. Изучение нового материала.

1. Необходимо построить биссектрису угла.

2. Разделить отрезок пополам.

Описание решения задачи на построение.

Учащиеся описания могут не делать.

Дан отрезок АВ, требуется разделить его на две равные части без линейки при помощи циркуля.

1. Откладывается отрезок АВ, циркулем замеряется его длина, это и будет радиус двух проводимых окружностей.

2. Из точки А провести окружность радиусом АВ.

3. Из точки В провести окружность того же радиуса.

4. Прямая, проведенная через точки пересечения этих окружностей, разделит искомый отрезок пополам.

IV. Решение задач.

Решить задачи 26, 29.

V. Итоги урока.

Выяснить различие между построением.

Задание на дом: пункты 45, 46; задачи 27, 30.

Урок 59
Построение перпендикулярной прямой

Цели: научить строить перпендикуляр к прямой при помощи циркуля.

Ход урока

I. Организационный момент.

Сформулировать тему и цели урока.

II. Проверить домашнюю работу.

Вызвать двоих учеников, чтобы они выполнили решение домашних задач на доске.

III. Изучение нового материала.

Через данную точку О провести прямую, перпендикулярную данной прямой а.

Существуют два случая.

1) Точка лежит на прямой а.

Рассмотреть рис. 103 в учебнике. Зарисовать его в тетрадь.

2) Точка не лежит на прямой а.

IV. Решение задач.

Решение задач 33, 35.

V. Итоги урока.

В чем различие построения, если точка лежит на прямой или точка не лежит на прямой?

Задание на дом: пункт 47; задачи 34, 36.

Урок 60
Геометрическое место точек.
Метод геометрических мест

Цели: ввести метод решения задач на построение, метод геометрических мест, научить применять его при решении задач на построение.

Ход урока

I. Организационный момент.

Сформулировать тему и цели урока.

II. Теоретический опрос.

Можно провести по вопросам из учебника.

III. Практическая работа

Эту работу лучше выполнять на листах А4, необходимо сделать описание построения. Вторая цифра в номере варианта отвечает за уровень сложности задания. Учащимся предоставить возможность выбрать задания самим.

Вариант 1.3

Разделить отрезок пополам.

Вариант 2.3

Построить биссектрису данного угла.

Вариант 3.4

Отложить от данной полупрямой в данную полуплоскость угол, равный данному углу.

Вариант 4.4

Через данную точку А, не принадлежащую прямой а, провести прямую, перпендикулярную прямой а.

Вариант 5.5

Построить треугольник по двум сторонам и углу между ними.

Вариант 6.5

Построить треугольник по данным стороне и двум прилежащим к ней углам.

Ответ к задаче варианта 5.5. Оформление может быть другим.

Аналогично можно выполнить задание из варианта 6.5.

IV. Изучение нового материала.

1. Геометрическим местом точек называется фигура, которая состоит из всех точек плоскости, обладающих определенным свойством.

2. Сформулировать теорему о геометрическом месте точек: геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная к отрезку, соединяющему эти точки, и проходящая через его середину.

3. Доказательство прочитать в учебнике. Требовать от учащихся воспроизводить доказательство необязательно.

4. Пункт 49 прочитать вслух, выделить основную мысль и записать ее в тетрадь.

5. Задачу 43, решенную в учебнике, разобрать.

V. Решение задач.

Решить задачу 41.

VI. Итоги урока.

– Что представляет собой геометрическое место точек, равноудаленных от двух данных?

– В чем заключается метод геометрических мест?

Задание на дом: пункты 48, 49; задачи 42, 44.

Урок 61
Геометрическое место точек.
Метод геометрических мест

Цели: закрепить метод решения задач на построение, метод геометрических мест, развивать навыки применения его при решении задач на построение.

Ход урока

I. Организационный момент.

Сформулировать тему и цели урока.

II. Анализ практической работы.

Объявить результаты практической работы; если допущены ошибки, то проанализировать их.

III. Решение задач.

1. Решить задачу 45.

2. Дополнительные задачи.

1) Построить окружность, диаметром которой является данный отрезок АВ.

2) Дан треугольник АВС. Постройте его биссектрису АМ.

3) Постройте угол, равный 30°.

4) Постройте прямоугольный треугольник АВС с прямым углом С, катетом АС, равным b, и углом В, равным углу МРК.

3. Решить задачу 50 из учебника.

IV. Итоги урока.

Задание на дом: повторить весь пройденный материал, задача 48.

Урок 62
Решение задач

Цели: закрепить полученные знания при решении задач, развивать логическое мышление.

Ход урока

I. Организационный момент.

Сформировать тему и цели урока.

II. Проверка домашней работы.

III. Решение задач.

1. Начертите: а) треугольник АВС и с помощью транспортира, линейки и угольника постройте в этом треугольнике биссектрису АD, медиану АМ, высоту АО;

б) тупоугольный треугольник и проведите в нем высоту.

2. Начертите равнобедренный треугольник, в котором угол, противолежащий основанию: а) острый; б) прямой; в) тупой.

3. Треугольник АВС равнобедренный с основанием АС. ÐС = 50°, ВО – высота. Определите углы треугольника АВО.

I. Итоги урока.

Задание на дом: подготовиться к контрольной работе. Повторить пройденный материал.

Дополнительная задача.

1. На боковых сторонах равнобедренного треугольника во внешнюю сторону построены равносторонние треугольники. Докажите, что отрезки, соединяющие вершины равносторонних треугольников (отличные от вершин равнобедренного треугольника) с серединой основания равнобедренного треугольника, равны.

2. На листе формата А4 решить следующую задачу.

Постройте равносторонний треугольник по стороне, за сторону можно принять любой отрезок.

Задания к практической работе для самоподготовки.

1. Необходимо повторить весь материал о задачах на построение, пункты 38, 42–49.

2. Постройте треугольник со сторонами 3,5 см; 4 см; 5 см.

3. Постройте треугольник со сторонами 4 см и 4,5 см и углом между ними 30°.

4. Постройте треугольник со стороной 4 см и прилежащими к ней углами в 45°, 35°.

5. Существует ли треугольник со сторонами:

а) 1 см, 2 см, 3 см; б) 5 см, 3 см, 10 см; в) 1 см, 8 см, 8 см?

6. Известны стороны равнобедренного треугольник: а) 3 см и 7 см; б) 4 см и 8 см; в) 6 см и 4 см. Чему равна третья сторона?

Урок 63
Решение задач

Цель: закрепить приобретенные знания при решении задач.

Ход урока

I. Организационный момент.

Сформулировать тему и цель урока.

II. Проверка домашней работы.

III. Практическая работа (второй номер соответствует уровню трудности).

Вариант 1.3

1. Разделить отрезок 5,5 см пополам.

2. Можно ли построить треугольник со сторонами 12 см, 13 см, 20 см?

Вариант 2.3

1. Построить биссектрису угла 45°.

2. Можно ли построить треугольник со сторонами 11 см, 5 см, 6 см?

Вариант 3.4

1. Отложить от полупрямой в верхнюю полуплоскость угол, равный углу 35°.

2. Можно ли построить треугольник со сторонами 10 см, 15 см, 30 см?

Вариант 4.4

1. Через точку А, не принадлежащую прямой а, провести прямую, перпендикулярную прямой а.

2. Известны стороны равнобедренного треугольника 6 см и 8 см. Чему равна третья сторона?

Вариант 5.5

1. Построить треугольник со сторонами 5 см и 4 см и углу между ними в 40°.

2. Известны стороны равнобедренного треугольника 7 см и 12 см. Чему равна третья сторона?

Вариант 6.5

1. Построить треугольник по стороне в 4 см и двум прилежащим к ней углам 30° и 45°.

2. Известны стороны равнобедренного треугольника 17 см и 12 см. Чему равна третья сторона?

Эта практическая работа может выполняться в группах при подготовке к контрольной работе.

IV. Итог урока.

Задание на дом: поработать с карточками, задания на которых не успели выполнить во время урока.

Урок 64
Контрольная работа № 5 по теме
«Геометрические построения»

Цель: проверить полученные знания.

Ход урока

I. Организационный момент.

II. Выполнение контрольной работы.

Вариант 1

1. Углы треугольника пропорциональны числам 2, 3, и 4. Найдите все углы треугольника.

2. Постройте равнобедренный треугольник по боковой стороне и углу при вершине.

3. АС – касательная, АВ – хорда окружности с центром в точке О, угол ВАС равен 75°. Чему равен угол АОВ?

4. АD и СЕ – биссектрисы равнобедренного треугольника АВС с основанием АС. Докажите, что треугольник АЕС равен треугольнику СDА.

Вариант 2

1. Угол при вершине равнобедренного треугольника на 30° больше угла при вершине основании. Найдите все углы треугольника.

2. Постройте равнобедренный треугольник по основанию и углу при основании.

3. АС – касательная, АВ – хорда окружности с центром в точке О, угол АОВ равен 70°. Чему равен угол ВАС?

4. АЕ и КМ – медианы равнобедренного треугольника АРК с основанием АК. Докажите, что треугольник АРЕ равен треугольнику КРМ.

III. Итоги урока.

Итоговое повторение курса геометрии
8 класса (4 часа)

Основная цель: систематизировать знания, умения и навыки учащихся, приобретенные в процессе изучения тем по геометрии.

На последних уроках, которые даны для повторения всего учебного материала, полезно сконцентрировать внимание на следующих темах.

1. Начальные геометрические сведения.

2. Треугольники: признаки равенства треугольников; равнобедренные треугольники, равносторонние треугольники; соотношения между сторонами и углами.

3. Параллельные прямые. Свойства параллельных прямых. Решение задач.

Уроки повторения изученного материала можно разнообразить. Например: на каждом из этих уроков решается ряд задач. Если эти задачи будут решены верно, то в конце последнего урока будет расшифрована фраза, касающаяся материала, изученного за весь год.

Для этого необходимо правильно выполнить задание, найти ответы в таблице, в столбиках рядом с буквой указано, сколько раз эта буква повторяется в данной фразе. После того как будут решены все задания, из полученных букв нужно составить фразу. В таблице есть и неправильные ответы, которые не используются.

После проведения трех уроков должно получиться следующее: «Планиметрия изучает фигуры на плоскости».

Окончание табл.

Урок 65
Повторение темы
«Начальные геометрические сведения»

Цель: систематизировать знания о начальных геометрических сведениях.

Ход урока

I. Организационный момент.

Сообщить названия тем, которые будут повторяться на данном уроке.

Объяснить, как работать с таблицей, более подготовленные учащиеся могут решать самостоятельно.

II. Решение задач.

1. Даны четыре прямые, каждые две из которых пересекаются. Сколько точек пересечения имеют эти прямые, если через каждую точку пересечения проходят только две прямые? (Ответ: 4.)

2. В одной полуплоскости относительно прямой МК отложены два угла: ÐМКС = 40° и ÐМКD = 60°. Чему равен ÐСКD? (Ответ: 20°.)

3. На отрезке КМ отметьте точку Р. Найдите длину отрезка РК, если известно,  что  он  в  4 раза  больше отрезка РМ, а отрезок КМ равен 20 см. (Ответ: 16 см.)

4. Найдите длину отрезка ВС, если известно, что АВ = 7 см, АС = 11 см и точка В лежит между А и С. (Ответ: 4 см.)

5. Найдите  градусную  меру  угла  АВС,  если ÐАВD = 52°, ÐВСD = 40° (Ответ: 92°.)

6. Найдите угол 4, если Ð1 = 130°, Ð2 = Ð3 (рис. 1). (Ответ: 50°.)

7. Один из смежных углов в 8 раз больше другого. Найдите меньший из этих углов. (Ответ: 20°.)

8. Луч ВМ является биссектрисой угла DВС, равного 74°. Найдите градусную меру угла СВМ. (Ответ: 37°.)

9. Через точку О отрезка АЕ проведен перпендикулярно ему луч ОС. Луч ОD – биссектриса угла ЕОС. Найдите ÐАОD. (Ответ: 135°.)

10. Найдите  угол,  образованный  биссектрисами двух смежных углов. (Ответ: 90°.)

11. Угол ab равен 120°, а угол ас равен 150°. Найдите угол bc. Для каждого из возможных случаев сделайте чертеж. (Ответ: 30° или 90°.)

12. Отрезок в 36 см разделен на четыре неравных друг другу части. Расстояние между серединами крайних частей равно 30 см. Найдите расстояние между серединами средних частей. (Ответ: 12 см.)

13. Три точки А, В, С лежат на одной прямой, АВ = 6 см, ВС = 10 см. Каким может быть расстояние АС? (Ответ: 16 см или 4 см.)

14. Сколько неразвернутых углов образуется при пересечении трех прямых, проходящих через одну точку? (Ответ: 12.)

15. Точка О лежит на отрезке АВ. Расстояние между точками А и В равно 24 см, а расстояние между точками О и А в два раза больше расстояния между точками О и В. Найдите расстояние между точками О и В. (Ответ: 8 см.)

III. Итоги урока.

Задание на дом: cоставить кроссворд так, чтобы в нем использовалось как можно больше слов из изученных тем.

Урок 66
Повторение темы
«Признаки равенства треугольников»

Цели: систематизировать знания о признаках равенства треугольников.

Ход урока

I. Организационный момент.

1. Сообщить названия тем, которые будут повторяться на уроке.

2. Повторить, как пользоваться таблицей.

II. Решение задач.

1. Учитывая пометки на рис. 1, укажите, какое равенство нужно добавить, чтобы треугольники были равны по первому признаку. (Ответ: ÐА = ÐD.)

2. Треугольник АВС – равнобедренный с основанием ВС. Используя рис. 2, найдите угол С. (Ответ: 50°.)

3. Периметр равнобедренного треугольника равен 42 см, боковая сторона  на 6 см  больше  основания.  Найдите  основание  этого  треугольника. (Ответ: 10 см.)

4. Используя рис. 3, найдите ÐОСВ. (Ответ: 40°.)

5. Используя рис. 3, найдите ÐАВО. (Ответ: 50°.)

6. В равнобедренном треугольнике основание больше боковой стороны на 2 см, но меньше суммы боковых сторон на 3 см. Найдите  сторону ВС. (Ответ: 5 см.)

7. В треугольнике АВС ÐА = 38°, ÐВ = 110°. На стороне АС отмечены точки D и Е так, что точка D лежит на стороне АЕ, ВD = DА, ВЕ = ЕС. Найдите ÐDBE. (Ответ: 40°.)

8. Основание равнобедренного треугольника равно 8 см, медиана, проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2 см больше периметра другого. Найдите боковую сторону равнобедренного треугольника. (Ответ: 10 см или 6 см.)

9. Периметр одного треугольника больше периметра другого треугольника. Могут ли эти треугольники быть равными. (Ответ: нет.)

10. В равнобедренном треугольнике АВС с основанием АС = 16 см отрезок ВО – биссектриса. Найдите СО. (Ответ: 8 см.)

III. Проверка кроссвордов.

1. Учащиеся обмениваются  кроссвордами и решают их.

2. Кроссворды сдаются на проверку.

IV. Итоги урока.

Задание на дом: повторить материал о сумме углов.

Дополнительная задача.

На основании ВС равнобедренного треугольника АВС отмечены точки М и D так, что ВМ = СD. Докажите, что:

а) DВАМ = DСАО;

б) треугольник АМО равнобедренный.

Урок 67
Повторение темы «Сумма углов треугольника.
Параллельные прямые»

Цели: систематизировать знания о сумме углов треугольника и о параллельных прямых.

Ход урока

I. Организационный момент.

Сформулировать названия тем, которые будут повторяться на уроке.

Напомнить, как заполнять таблицу.

II. Проверка домашней работы.

III. Решение задач.

1. Найдите угол М четырехугольника КМОD, если МК || OD, ÐМОК = 40°, ÐKOD = 80°. (Ответ: 60°.)

2. Один  из  двух  внутренних  односторонних  углов  при  параллельных  прямых  и  секущей  в 5 раз  больше  другого. Найдите его величину. (Ответ: 150°.)

3. Прямая, параллельная стороне АВ треугольника АВЕ, пересекает сторону АЕ в точке О и сторону ВЕ в точке Р. Найдите угол РОЕ, если ÐА = 65°. (Ответ: 65°.)

4. СН – высота, проведенная к гипотенузе прямоугольного треугольника. Найдите угол АСН, если ÐВ = 40°. (Ответ: 40°.)

5. Дан  треугольник  МОК, ÐК = 65°, ВС || МК, ВС = ОВ. Найдите ÐО. (Ответ: 65°.)

6. Найдите угол А треугольника АВС, если он на 20° больше угла С, а внешний угол при вершине В равен 108°. (Ответ: 64°.)

7. Дан DАВС, в треугольнике проведена медиана АМ, АМ = АВ = 10 см, ВС = 20 см. Найдите ÐАМО. (Ответ: 120°.)

8. В  треугольнике  МОК, ÐО = 84°.  На стороне МК  отмечена  точка А, а на стороне ОК  отмечена  точка В,  причем  АВ || МО.  Найдите  ÐАВК.  (Ответ: 84°.)

9. Прямые а и с параллельны. Найдите угол 2, если Ð1 = 124°. См. рис.1. (Ответ: 56°.)

IV. Итоги урока.

Задание на дом: подготовиться к итоговой контрольной работе за курс 7 класса.

Урок 68
Итоговая контрольная работа

Цели: проверить знания, умения и навыки учащихся по пройденному материалу.

Ход урока

I. Организационный момент.

II. Решение контрольной работы.

Вариант 1

1. Прямые а и с параллельны, угол 1 равен 40°. Найдите угол 2 (см. рис. 1).

2. Треугольник АВС – равнобедренный с основанием ВС, отрезок ВК – его биссектриса. Найдите ÐАКВ, если ÐС = 70°.

3. Найдите угол В треугольника ВСЕ, если он на 30° меньше угла С, а внешний угол при вершине Е равен 130°.

4. Найдите угол Р треугольника РМD, если ÐD = 45°, ÐАКD = 85°, а прямые КА и РМ параллельны.

5. В треугольнике АВС и АЕС известны элементы: ÐСАВ = 45°, ÐАВС = 70°, ÐСАЕ = 65°,  АВ = 6 см. Какое равенство верно?

а) АЕ = 6 см;                   в) СЕ = 6 см;

б) АС = 6 см;                  г) ВС = 6 см.

6. Дан треугольник АВС с прямым углом в точке А, ÐС = 30°, АВ = 6 см. Какое равенство верно?

а) АС = 6 см;                 в) ВС = 12 см;

б) АС = 12 см;               г) ВС = 6 см.

Ответы: 1) 40°, 2) 105°, 3) 50°, 4) 50°, 5) в, 6) в.

Вариант 2

1. Прямые а и с параллельны, угол 1 равен 70°. Найдите угол 2 (см. рис. 2).

2. Треугольник АВС – равнобедренный с основанием ВС, отрезок ВК – его высота. Найдите ÐАВК, если ÐС = 70°.

3. Найдите угол В треугольника АВЕ, если он на 30° меньше угла Е, а угол А равен 80°.

4. Найдите угол КСЕ, если в треугольнике ОКМ, ÐО = 50°, ÐМ = 60°, а прямые СЕ и КМ параллельны.

5. В треугольниках АВС и ВАЕ известны элементы: ÐАВС = 30°, ÐВАС = 70°, ÐВЕА = 80°, ÐВАЕ = 30°, АС = 4 см. Какое равенство неверно?

а) АЕ = 4 см;                     в) АВ = 4 см;

б) ВЕ = 4 см;                    г) ВС = 4 см.

6. Дан треугольник АВС, ÐВ = 90°, ÐС = 45°, АВ = 6 см. Какое равенство верно?

а) АС = 6 см;                      в) АС = 12 см;

б) ВС = 12 см;                   г) ВС = 6 см.

Ответы: 1) 110°, 2) 50°, 3) 35°, 4) 110°, 5) б, 6) г.

III. Итог урока.

 

Скачано с www.znanio.ru