Внеурочная деятельность/интеллектуальное направление «Почемучка»

Тема: Интересные приемы устного счёта.

Цель: познакомить учащихся с интересными приёмами устных вычислений, помочь запомнить и освоить данные приёмы с целью практического их исмпользования.

Ход занятия.

1.       Орг. момент

2.       Введение в тему. Актуализация. Нпацеливание

 Во все времена математика была и остается одним из основных предметов в школе, потому что математические знания необходимы всем людям. Не каждый школьник, обучаясь в школе, знает, какую профессию он выберет в будущем, но каждый понимает, что математика необходима для решения многих жизненных задач: расчеты в магазине, оплата за коммунальные услуги, расчет семейного бюджета и т.д. Кроме того, всем школьникам  необходимо сдавать экзамены в 9-м классе и в 11-м классе, а для этого, обучаясь с 1-го класса,  необходимо качественно осваивать математику и прежде всего, нужно научиться считать. 

Можно ли представить себе мир без чисел? Без чисел ни покупки не сделаешь, ни времени не узнаешь, ни номера  телефона не наберёшь. А космические корабли, лазеры и все другие технические достижения?! Они были бы попросту невозможны,  если бы не наука о числах.

Две стихии господствуют в математике – числа и фигуры с их бесконечным многообразием свойств и взаимосвязей.

Цель: изучить приемы быстрого счета, показать необходимость их применения для упрощения вычислений.

3.       Работа по теме

КАК ВОЗНИКЛИ ЧИСЛА

Подсчитывать предметы люди научились ещё в древнем каменном веке - палеолите, десятки тысяч лет назад. Как это происходило? Сначала люди лишь на глаз сравнивали разные количества одинаковых предметов. Они могли определить, в какой из двух куч больше плодов, в каком стаде больше оленей и т.д. Если одно племя меняло пойманных рыб на сделанные людьми другого племени каменные ножи, не нужно было считать, сколько принесли рыб и сколько ножей. Достаточно было положить рядом с каждой рыбой по ножу, чтобы обмен между племенами состоялся.

Чтобы с успехом заниматься сельским хозяйством, понадобились арифметические знания. Без подсчета дней трудно было определить, когда надо засевать поля, когда начинать полив, когда ждать потомства от животных. Надо было знать, сколько овец в стаде, сколько мешков зерна положено в амбары.
       И вот более восьми тысяч лет назад древние пастухи стали делать из глины кружки – по одному на каждую овцу. Чтобы узнать, не пропала ли за день хоть одна овца, пастух откладывал в сторону по кружку каждый раз, когда очередное животное заходило в загон. И только убедившись, что овец вернулось столько же, сколько было кружков, он спокойно шел спать. Но в его стаде были не только овцы – он пас и коров, и коз, и ослов. Поэтому пришлось сделать из глины и другие фигурки. А земледельцы с помощью глиняных фигурок вели учет собранного урожая, отмечая, сколько мешков зерна положено в амбар, сколько кувшинов масла выжато из оливок, сколько соткано кусков льняного полотна. Если овцы приносили приплод, пастух прибавлял к кружкам новые, а если часть овец шла на мясо, несколько кружков приходилось убирать. Так, еще не умея считать, занимались древние люди арифметикой.

Затем в человеческом языке появились числительные, и люди смогли называть число предметов, животных, дней. Обычно таких числительных было мало. Например, у племени реки Муррей в Австралии было два простых числительных: энэа (1) и петчевал (2). Другие числа они выражали составными числительными: 3= «петчевал–энэа», 4 «петчевал–петчевал» и т. д. Ещё одно австралийское племя – камилороев имело простые числительные мал (1), булан (2), гулиба (3) . И здесь другие числа получались сложением меньших: 4=«булан–булан», 5=«булан–гулиба», 6=«гулиба–гулиба» и т.д.

У многих народов название числа зависело от подсчитываемых предметов. Если жители островов Фиджи считали лодки, то число 10 называли «боло»; если они считали кокосовые орехи, то число 10 называли «каро». Точно так же поступали живущие на Сахалине у берегах Амура нивхи. Ещё в XIX веке одно и то же число они называли разными словами, если считали людей, рыб, лодки, сети, звёзды, палки.

Мы и сейчас используем разные неопределённые числительные со значением «много»: «толпа», «стадо», «стая», «куча», «пучок» и другие.

С развитием производства и торгового обмена люди стали лучше понимать, что общего у трёх лодок и трёх топоров, десяти стрел и десяти орехов. Племена часто вели обмен «предмет за предмет»; к примеру, обменивали 5 съедобных кореньев на 5 рыб. Становилось ясно, что 5 одно и то же и для кореньев, и для рыб; значит, и называть его можно одним словом.

Постепенно люди начали использовать для счёта камешки, палочки, части собственного тела. Вот как известный русский учёный Н.Н. Миклуха–Маклай описывал счёт папуасов: «Папуас загибает один за другим пальцы руки, причём издаёт определённый звук, например «бе, бе, бе…». Досчитав до пяти, он говорит:  «Ибон–бе» (рука). Затем он загибает пальцы другой руки, снова повторяя «бе, бе…», пока не дойдёт до «ибон–али» (две руки). Затем он идёт дальше, приговаривая «бе, бе…», пока не дойдёт до «самба–бе» (одна нога) и «самба–али» (две ноги). Если нужно считать дальше, папуас пользуется пальцами рук и ног кого – нибудь другого».

Похожие способы счёта применяли и другие народы. Так возникли нумерации, основанные на счёте пятёрками, десятками, двадцатками.

До сих пор я рассказывал об устном счёте. А как записывали числа? Поначалу, ещё до возникновения письменности, использовали зарубки на палках, насечки на костях, узелки на верёвках. Найденная волчья кость в Дольни – Вестонице (Чехословакия), имела 55 насечек, сделанных более 25 000 лет назад.

Когда появилась письменность, появились и цифры для записи чисел. Сначала цифры напоминали зарубки на палках: в Египте и Вавилоне, в Этрурии и Финики, в Индии и Китае небольшие числа записывали палочками или чёрточками. Например, число 5 записывали пятью палочками. Индейцы ацтеки и майя вместо палочек использовали точки. Затем появились специальные знаки для некоторых чисел, таких, как 5 и 10 .

В то время почти все нумерации были не позиционными, а похожими на римскую нумерацию. Лишь одна вавилонская шестидесятеричная нумерация была позиционной. Но и в ней долго не было нуля, а также запятой, отделяющей целую часть от дробной. Поэтому одна и та же цифра могла означать и 1, и 60, и 3600. Угадывать значение числа приходилось по смыслу задачи.

За несколько столетий до новой эры изобрели новый способ записи чисел, при котором цифрами служили буквы обычного алфавита. Первые 9 букв обозначали числа десятки 10, 20,…, 90, а ещё 9 букв обозначали сотни. Такой алфавитной нумерацией пользовались до 17 в. Чтобы отличить «настоящие» буквы от чисел, над буквами–числами ставили чёрточку (на Руси эта чёрточка называлась «титло»).

Во всех этих нумерациях было очень трудно выполнить арифметические действия. Поэтому изобретение в VI веке индийцами десятичной позиционной нумерации по праву считается одним из крупнейших достижений человечества. Индийская нумерация и индийские цифры стали известны в Европе от арабов, и обычно их называют арабскими.

При записи дробей ещё долгое время целую часть записывали в новой десятичной нумерации, а дробную – в шестидесятеричной. Но в начале XV в. самаркандский математик и астроном аль–Каши стал употреблять в вычислениях десятичные дроби. 

Числа, с которыми мы работаем с положительными и отрицательными числами. Но, оказывается,  что это не все числа, которые используют в математике и других науках. И узнать о них можно не дожидаясь старшей школы, а гораздо раньше, если изучать историю возникновения чисел в математике.

Интересные приёмы устных вычислений

1. Умножение на 11

Умножать на 11 чуть сложнее, чем умножать на 10. Закономерность здесь такая:

53 х 11 = 583
Шаг 1 — Складываем две цифры двузначного числа: 5 + 3 = 8
Шаг 2 — Помещаем результат между двумя числами двузначного числа: 583

59 х 11 = 649
Шаг 1 — 5 + 9 = 14
Шаг 2 — Перекидываем единицу налево, если сумма на предыдущем шаге оказалась больше 9: 5 + 1 = 6 (справа остается второй символ, в данном случае это четверка)
Шаг 3 — На первый символ мы единицу уже перекинули, получили 6. Далее у нас осталась 4, которую ставим в центр, и дописываем 9: 649

2. Быстрое возведение в квадрат

Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5.

85 х 85 = 7225
Шаг 1 — Умножаем первую цифру на первую цифру, увеличенную на единицу: 8 x (8 + 1) = 72
Шаг 2 — Дописываем к получившемуся результату 25: 7225

45 x 45 = 2025
Шаг 1 — 4 х (4 + 1) = 20
Шаг 2 — 2025

3. Умножение на 5

Большинство людей очень просто запоминает таблицу умножения на 5, но, когда приходится иметь дело с большими числами, сделать это становится сложнее. Или нет? Этот прием невероятно прост.

Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5.

Это срабатывает всегда:
2682×5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
13410
Давайте попробуем другой пример:
5887×5
2943,5 (дробное число, пропустите запятую, добавьте 5)
29435

4. Умножение на 9

Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.

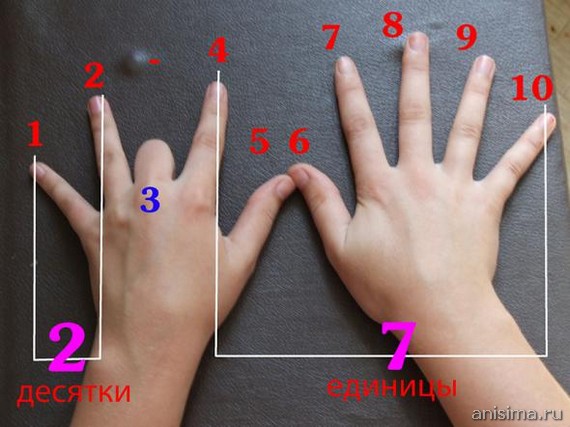
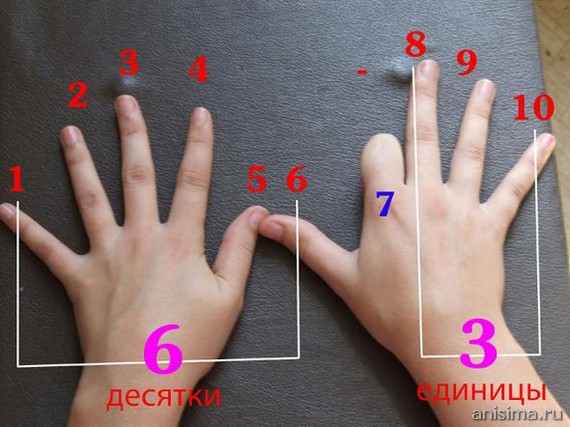
5. Умножение на 4

Это очень простой прием, хотя очевиден лишь для некоторых. Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2:
58×4 = (58×2) + (58×2) = (116) + (116) = 232

6. Подсчет чаевых

Если вам нужно оставить 15% чаевых, есть простой способ сделать это.

Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75

И, как следствие):  чтобы умножить число на 1,5 нужно к исходному числу прибавить его половину. Например,

34*1,5 = 34+17=51

125*1,5= 125+62,5=187,5

7. Сложное умножение

Если вам нужно умножать большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ:
32×125 все равно, что:
16×250 все равно, что:
8×500 все равно, что:
4×1000 = 4,000

8. Деление на 5

На самом деле делить большие числа на 5 очень просто. Все, что нужно,— просто умножить на 2 и перенести запятую: 195 / 5
Шаг1: 195×2 = 390
Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5
Шаг1: 2978×2 = 5956
Шаг2: 595,6

9. Вычитание из 1000

Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10:

1000-648

Шаг1: от 9 отнимите 6 = 3
Шаг2: от 9 отнимите 4 = 5
Шаг3: от 10 отнимите 8 = 2
Ответ: 352

И, напоследок, несколько математических трюков:

Интересные результаты:

1 х 1 = 1
11 х 11 = 121
111 х 111 = 12321
1111 х 1111 = 1234321
11111 х 11111 = 123454321
111111 х 111111 = 12345654321
1111111 х 1111111 = 1234567654321
11111111 х 11111111 = 123456787654321
111111111 х 111111111 = 12345678987654321

1 х 9 + 2 = 11
12 х 9 + 3 = 111
123 х 9 + 4 = 1111
1234 х 9 + 5 = 11111
12345 х 9 + 6 = 111111
123456 х 9 + 7 = 1111111
1234567 х 9 + 8 = 11111111
12345678 х 9 + 9 = 111111111
123456789 х 9 + 10 = 1111111111

9 х 9 + 7 = 88
98 х 9 + 6 = 888
987 х 9 + 5 = 8888
9876 х 9 + 4 = 88888
98765 х 9 + 3 = 888888
987654 х 9 + 2 = 8888888
9876543 х 9 + 1 = 88888888
98765432 х 9 + 0 = 888888888

1 х 8 + 1 = 9
12 х 8 + 2 = 98
123 х 8 + 3 = 987
1234 х 8 + 4 = 9876
12345 х 8 + 5 = 98765
123456 х 8 + 6 = 987654
1234567 х 8 + 7 = 9876543
12345678 х 8 + 8 = 98765432
123456789 х 8 + 9 = 987654321

Любимая цифра.

Предложите  задумать свою любимую цифру. А теперь выполните умножение (на калькуляторе) числа 15873 на любимую цифру, умноженную на 7. Например, если любимая цифра 5, то умножить нужно на 35. Получится произведение, записанное только любимой цифрой.

Возможен и второй вариант: умножить число 12345679 на любимую цифру, умноженную на 9, в нашем случае это число 45.

Объяснение этого фокуса достаточно простое: если умножить 15873 на 7, то получится 111111, а если умножить 12345679 на 9, то получится 111111111.

Угадать возраст.

Умножаем число своих лет на 10, затем любое однозначное число умножить на 9,  из первого произведения вычесть второе и сообщить полученную разность. В этом числе “фокусник” должен цифру единиц сложить с цифрой десятков – получится число лет.

Всегда девятка

Предложите кому-нибудь написать число из трех разных цифр, под ним — написать число из этих же цифр, но в обратном порядке. Затем вычесть меньшее из большего. Когда зритель это сделает, скажите ему, что в середине числа стоит девятка.

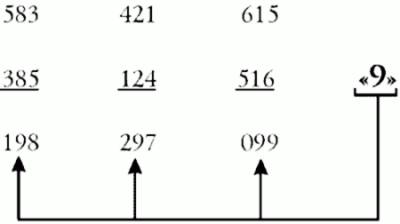
Секрет фокуса: Вы будете правы, потому что девятка всегда будет в середине независимо от того, какие цифры написаны.

4.       Подведение итогов. Рефлексия

5.       Скачано с www.znanio.ru